Introduction to Functions (Edexcel GCSE Maths)

Revision Note

Test yourself Flashcards

Written by: Mark Curtis

Reviewed by: Dan Finlay

Did this video help you?

Introduction to Functions

What is a function?

A function is a combination of one or more mathematical operations that takes a set of numbers and changes them into another set of numbers
The numbers being put into the function are often called the inputs
The numbers coming out of the function are often called the outputs
A function may be thought of as a mathematical “machine”
- For example, for the function “double the number and add 1”, the two mathematical operations are "multiply by 2 (×2)" and "add 1 (+1)"
  - Putting 3 in to the function would give 2 × 3 + 1 = 7
  - Putting -4 in would give 2 × (-4) + 1 = -7
  - Putting $x$ in would give $2 x + 1$

What is function notation?

A function, f, with input $x$ can be written as $f (x) = . . .$
- Letters other than f can be used
  - The letters g, h and j are common but any letter can be used
  - Typically, a new letter will be used to define a new function in a question
For example, the function with the rule “triple the number and subtract 4” would be written
- $f (x) = 3 x - 4$
In such cases, " $x$ " is the input and " $f (x)$ " is the output
Sometimes functions don’t have names like f and are just written as y = …
- E.g. $y = 3 x - 4$

How does a function work?

A function has an input $x$ and an output $f (x)$
- If the input is 2, then the output is $f (2)$
- If the input is $m$ , then the output is $f (m)$
- If the input is $t + 5$ , then the output is $f (t + 5)$
  - You cannot simplify this output any further
If the function is known, the output can be calculated
- For example, given the function $f (x) = 2 x + 1$
  - $f (3) = 2 \times 3 + 1 = 7$
  - $f (- 4) = 2 \times (- 4) + 1 = - 7$
  - $f (a) = 2 a + 1$

If the output is known, an equation can be formed and solved to find the input
- For example, given the function $f (x) = 2 x + 1$
  - If $f (x) = 15$ , then form an equation by replacing $f (x)$ with $2 x + 1$
  - $2 x + 1 = 15$
  - Solving this equation gives an input of 7
Note that $f (x) = 15$ and $f (15)$ are very different things:
- $f (x) = 15$ means an input of $x$ gives an output of 15
- $f (15)$ means substitute the input 15 into the function

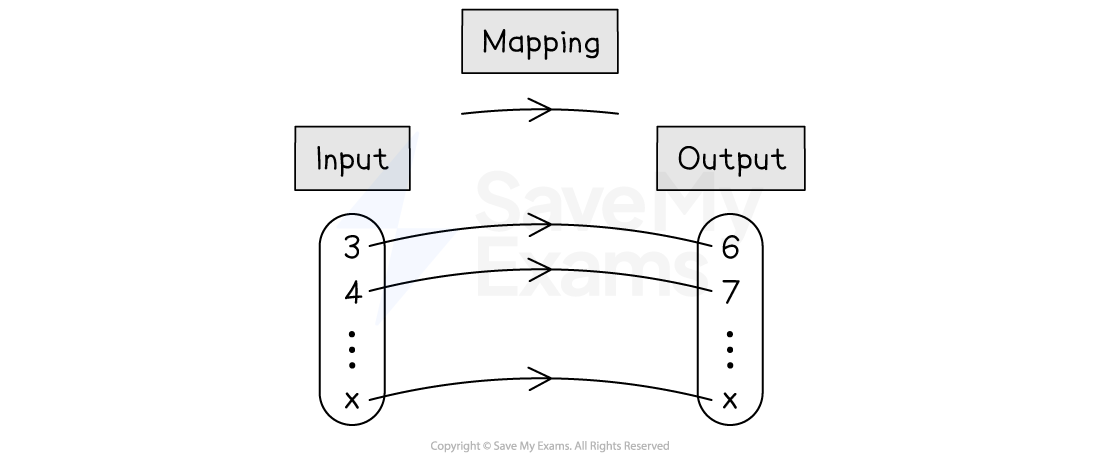
What is a mapping diagram?

A mapping diagram shows a set of different inputs going into the function to become a set of different outputs
- Transforming inputs into outputs is called mapping
For example, a mapping diagram for the function $f (x) = x + 3$ where $x \geq 3$ could be shown as:

Diagram showing a set of input numbers being mapped over to a set of output values.

Worked Example

A function is defined as $f (x) = 3 x^{2} - 2 x + 1$ .

(a) Find $f (7)$ .

The input is $x = 7$ , so substitute 7 into the expression everywhere you see an $x$

$f (7) = 3 {(7)}^{2} - 2 (7) + 1$

Calculate

$\begin{array}{rcl} f (7) & = & 3 (49) - 14 + 1 \\ = & 147 - 14 + 1 \end{array}$

$f (7) = 134$

(b) Find $f (x + 3)$ , giving your answer in the form $a x^{2} + b x + c$ where $a$ , $b$ and $c$ are integers to be found.

The input is $(x + 3)$ so substitute $(x + 3)$ into the expression everywhere you see an $x$
This is like replacing $x$ with $(x + 3)$

$f (x + 3) = 3 {(x + 3)}^{2} - 2 (x + 3) + 1$

Expand the brackets and simplify
Use that ${(x + 3)}^{2} = (x + 3) (x + 3)$
Be careful with negative signs

$\begin{array}{rcl} f (x + 3) & = & 3 (x^{2} + 6 x + 9) - 2 (x + 3) + 1 \\ = & 3 x^{2} + 18 x + 27 - 2 x - 6 + 1 \\ = & 3 x^{2} + 16 x + 22 \end{array}$

$f (x + 3) = 3 x^{2} + 16 x + 22$

(a = 3, b = 16, c = 22)

A second function is defined by $g (x) = 3 x - 4$ .

This is not saying substitute 16 into the function
It says that an input $x$ is substituted into $g$ giving the output -16
To find the input, form an equation by replacing $g (x)$ with $3 x - 4$

$\begin{array}{rcl} 3 x - 4 & = & - 16 \end{array}$

Solve the equation (for example, by adding 4 to both sides, then dividing by 3)

$\begin{array}{rcl} 3 x - 4 & = & - 16 \\ 3 x & = & - 12 \\ x & = & - \frac{12}{3} \end{array}$

$x = - 4$

Last updated: 17 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: