3D Pythagoras & Trigonometry (AQA GCSE Maths) : Revision Note
3D Pythagoras & Trigonometry
How do I use Pythagoras' theorem in a 3D shape?
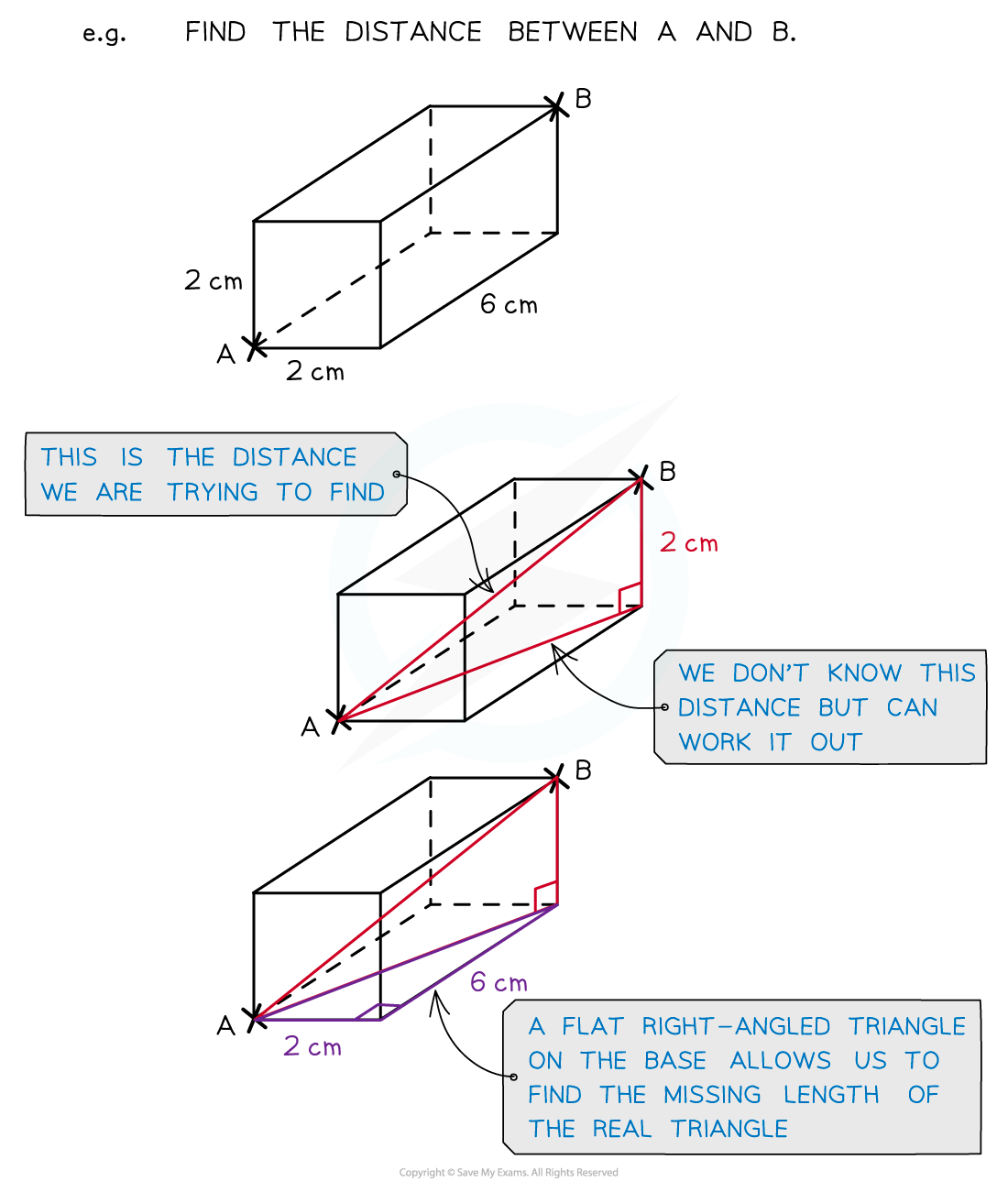
You can often find right-angled triangles within 3D shapes
If two sides of the triangle are known, you can use Pythagoras’ theorem

Is there a 3D version of the Pythagoras' theorem formula?
There is a 3D version of Pythagoras’ theorem:
is the distance between two points
and
are the distances in the three different perpendicular directions between the two points

However, all 3D situations can be broken into two 2D problems
Form two right-angle triangles
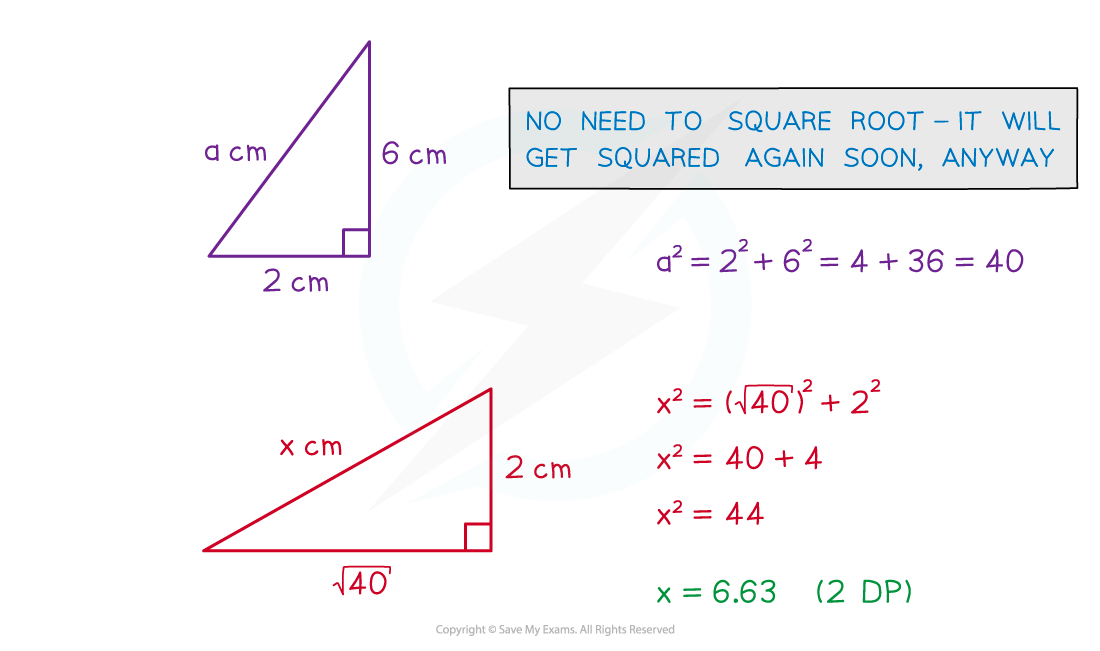
Examiner Tips and Tricks
You are not given the 3D Pythagoras formula in the exam
You can always split 3D problems into two 2D problems (which don't need this formula)
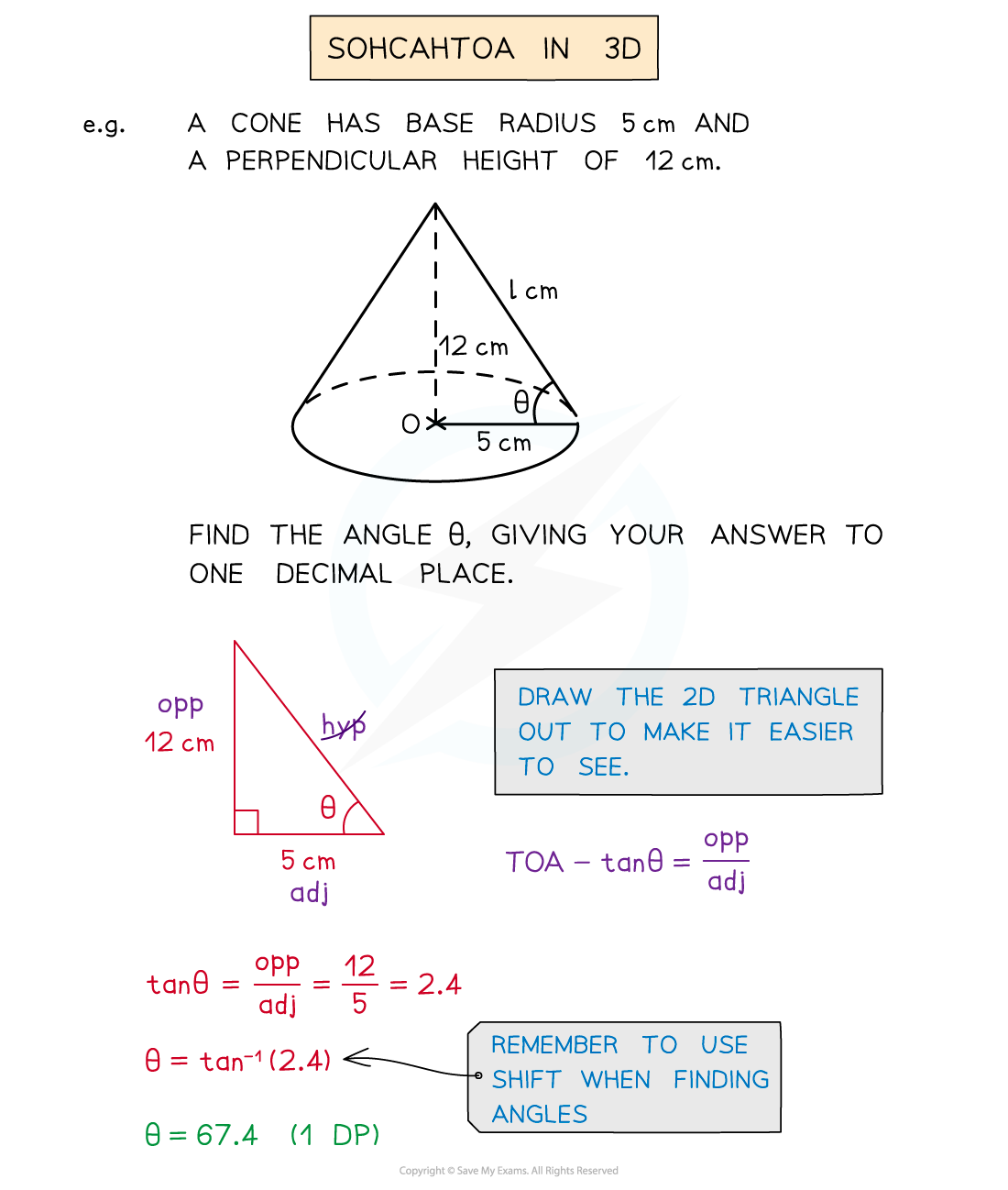
How do I use SOHCAHTOA in 3D?
Again, look for right-angled triangles to use with SOHCAHTOA
You may need combinations of triangles that lead to the missing side or angle
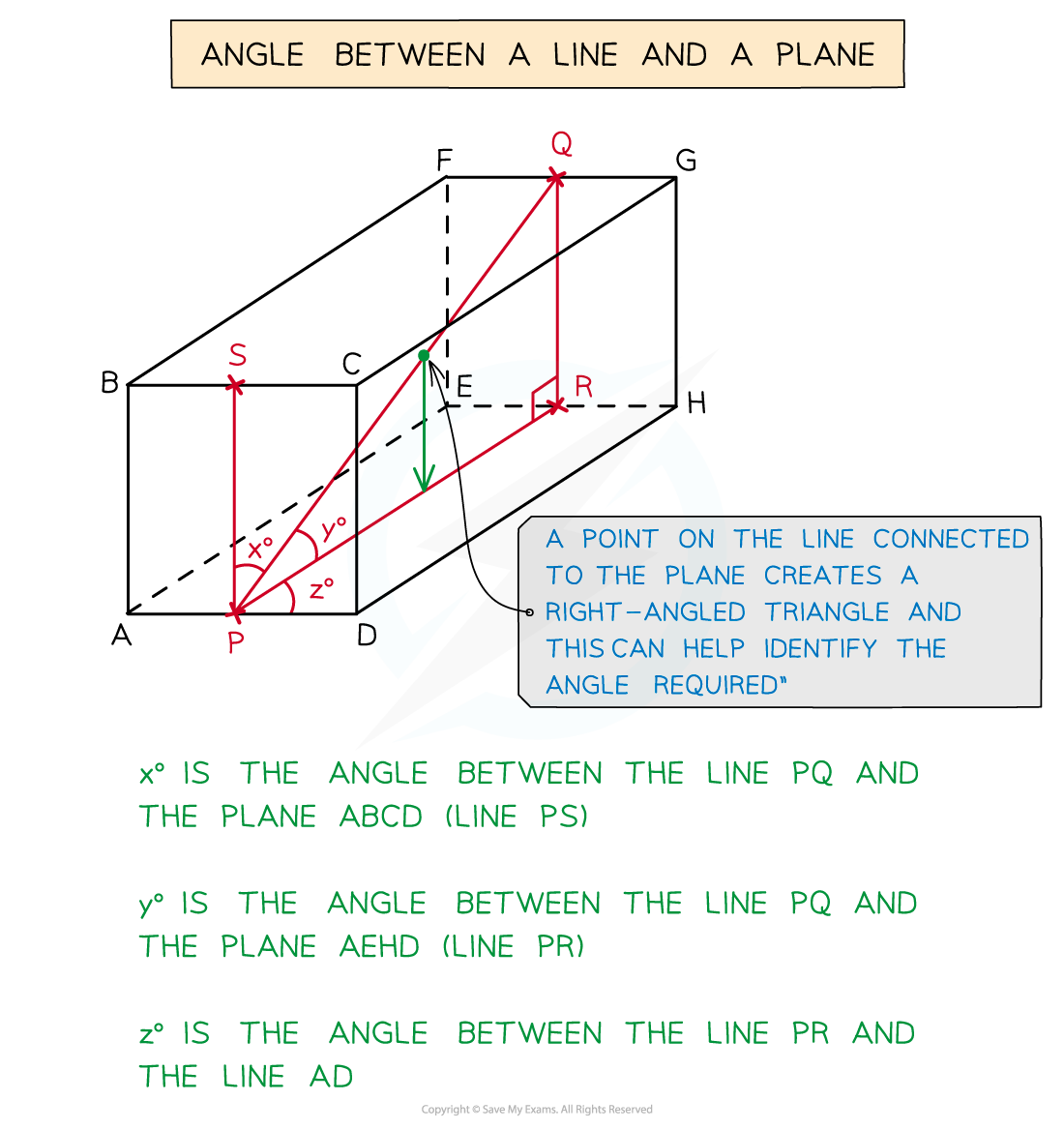
How do I find the angle between a line and a plane?
To find the angle between a line and a plane:
first identity the plane in the question
then draw on the line in the question (if it is not already drawn on)
form a right-angled triangle between the line and plane
The height of the triangle must be perpendicular to the plane
then use SOHCAHTOA
The angle between a line and a plane is sometimes not obvious
If unsure, put a different point on the same line and see if it helps
Try to create a right-angled triangle
Some people like to imagine the line as a fishing rod, from which they lower the hook (and fishing line) vertically down to the plane!
Others like to imagine they are sitting inside the 3D object, looking around it (like corners of a room)
How do I apply 3D Pythagoras and trigonometry to more complicated problems?
Always split up a complicated problem into 2D right-angled triangles
Some questions may requires more than one 2D right-angled triangle
Some 2D triangles on the diagram are still drawn in 3D
It helps to redraw these 2D triangles flat on the page (not at angles)
You can then spot any uses of Pythagoras' theorem and SOHCAHTOA

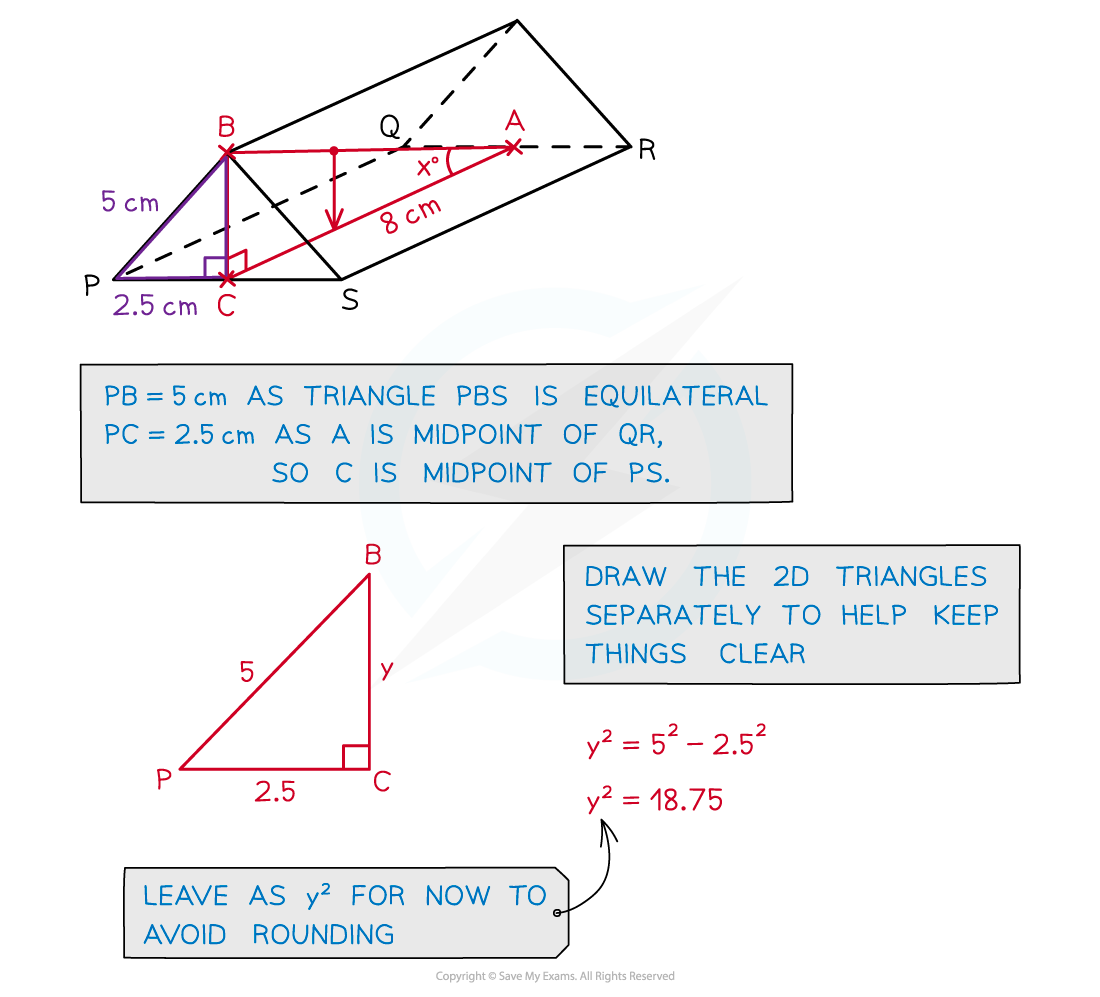
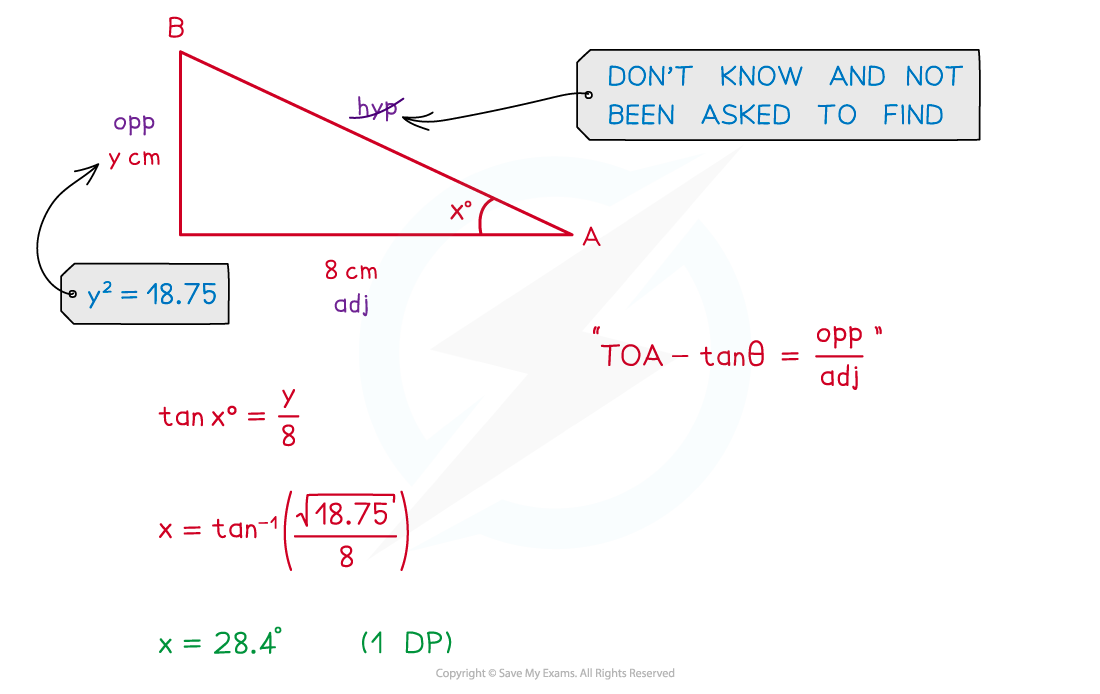
Examiner Tips and Tricks
If you are stuck in the exam with a complicated 3D diagram, it is always better to just start finding any lengths and angles in the shape, as:
these may end up being useful
you may score more marks than if you had left the question blank
Worked Example
A pencil is being put into a cuboid shaped box.
The box has dimensions 3 cm by 4 cm by 6 cm.
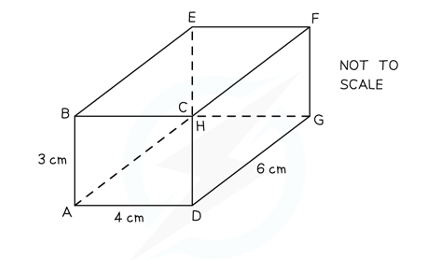
(a) Find the length of the longest pencil that can fit inside the box.
The longest possible pencil will fit between diagonally opposite vertices, e.g. AF
Form a 2D right-angled triangle, such as triangle ABF
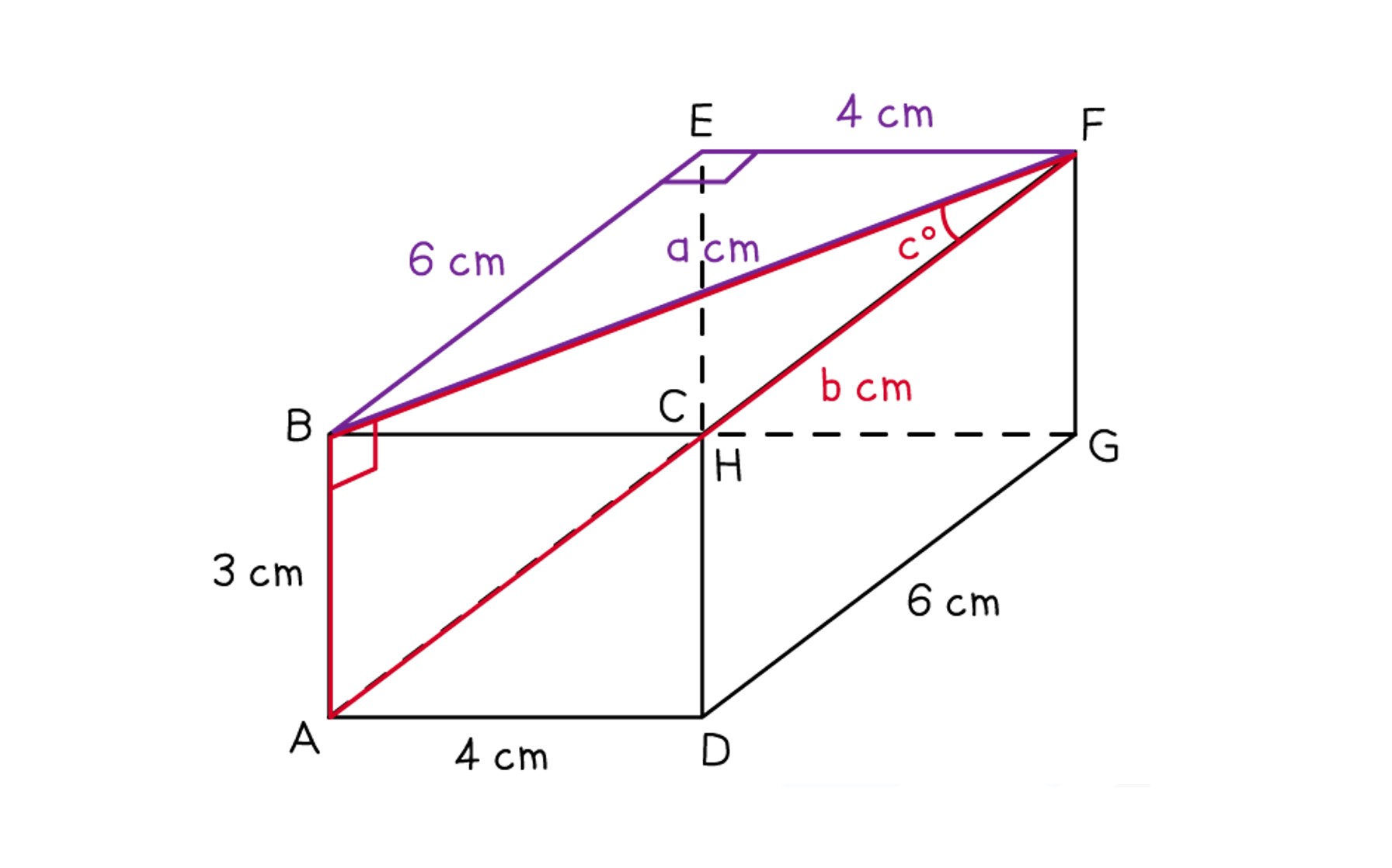
Method 1
To find the length AF, there are a few different options
One option is to find length BF (from triangle BEF) then AF (from triangle ABF)
Draw triangle BEF flat and use Pythagoras' theorem to find BF
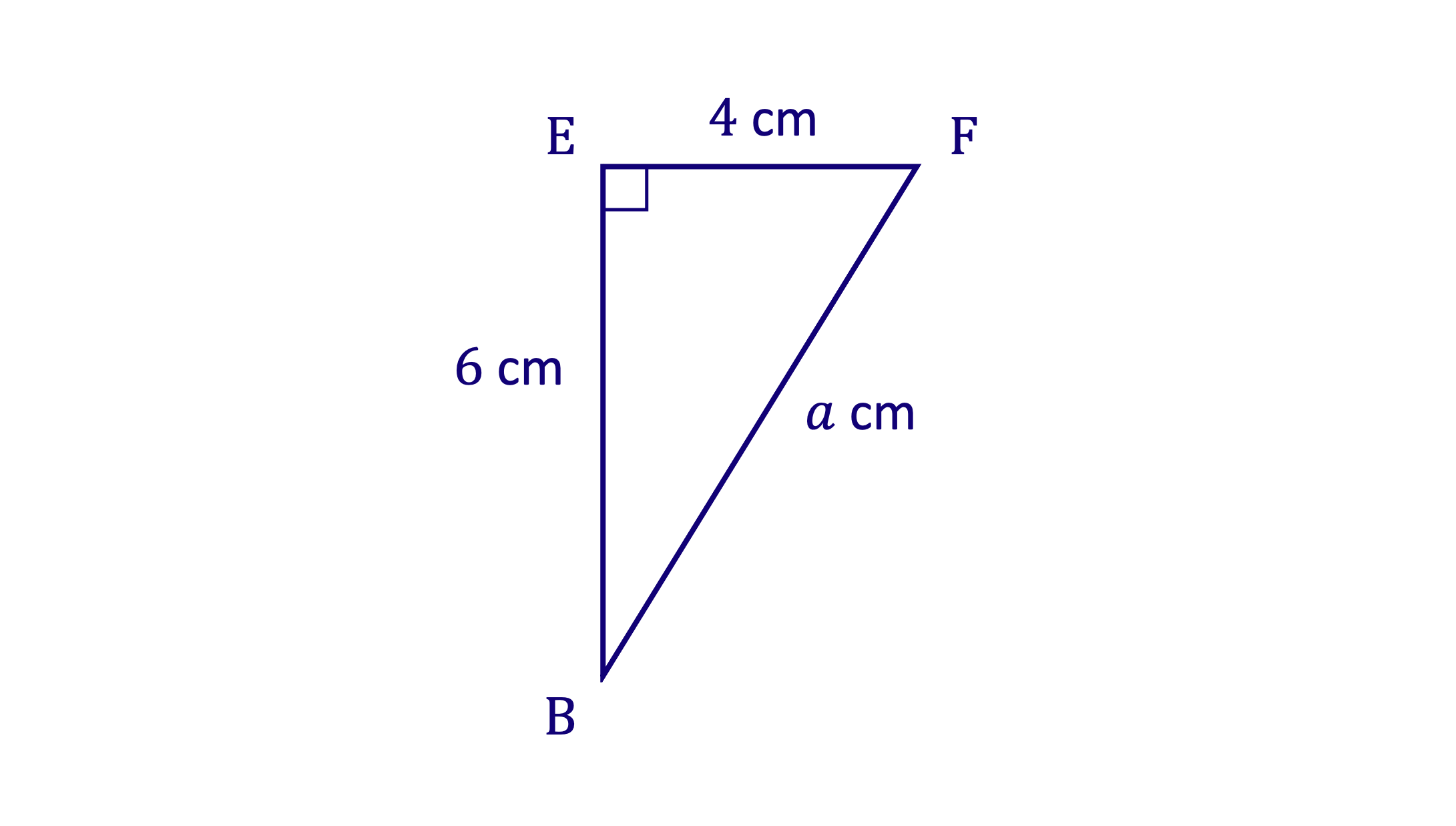
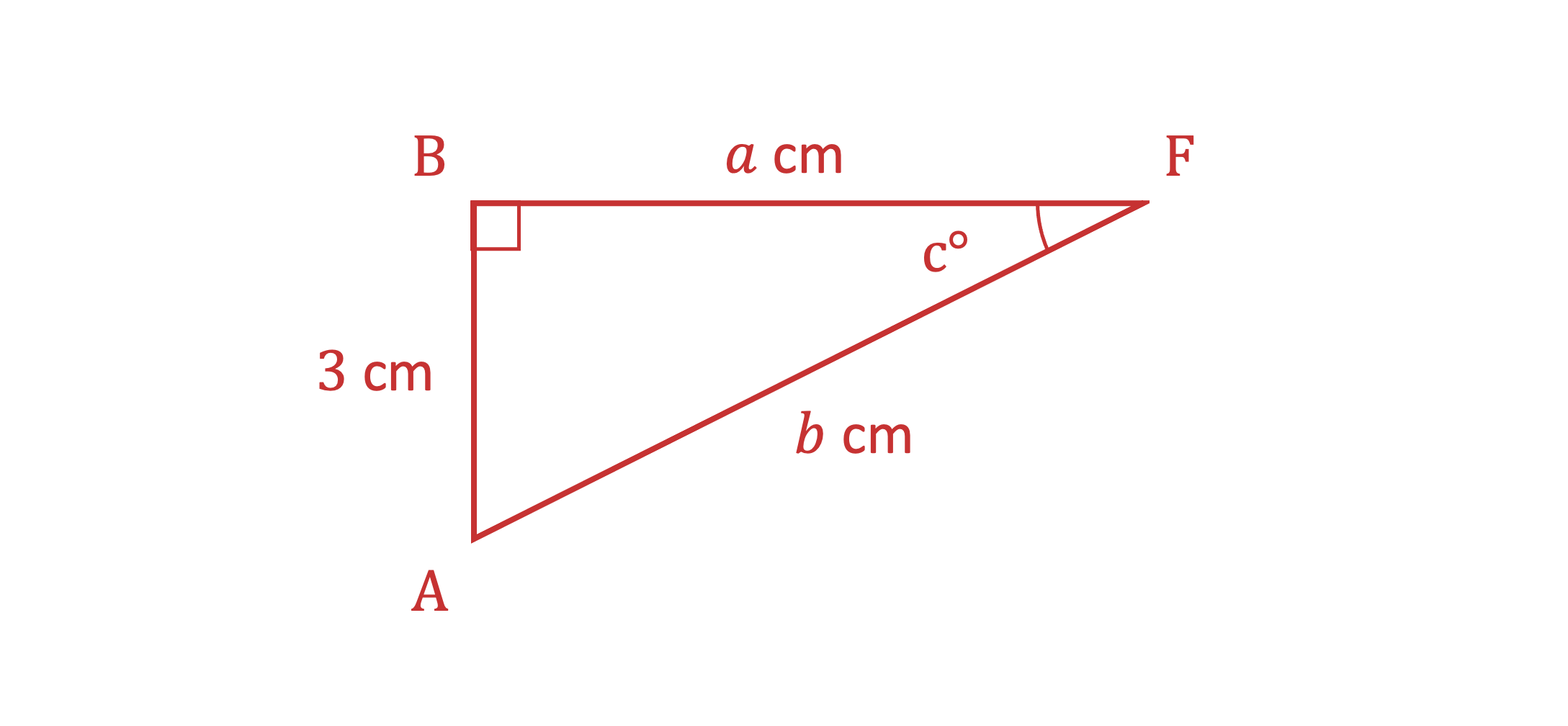
Draw triangle ABF flat and use Pythagoras' theorem to calculate AF
The longest pencil that can fit inside the box is 7.81 cm (to 3 s.f.)
Method 2
Apply the 3D version of Pythagoras’ theorem:
The distance in the x direction is 4 cm
The distance in the y direction is 6 cm
The distance in the z direction is 3 cm
The longest pencil that can fit inside the box is 7.81 cm (to 3 s.f.)
(b) Find the angle that the pencil would make with the plane BEFC.
The plane BEFC is the horizontal top surface of the box
To see the angle between AF and the plane, form a triangle with side AB (which is a height perpendicular to the plane)
The angle needed is marked

Triangle ABF is the 2D triangle needed, but it is currently drawn in 3D
Draw triangle ABF flat on the paper and write on the lengths from part (a)

This is now ready for SOHCAHTOA
We know all three sides so could use any trig ratio, for example
Use this to find angle
The angle between plane BEFC and the pencil is 22.6º (to 1 d.p.)

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

