Finding Areas under Graphs (AQA GCSE Maths): Revision Note
Exam code: 8300
Did this video help you?
Finding areas under graphs
How do I estimate the area under a graph?
To find an estimate for the area:
Split area into vertical strips
Draw straight lines between the tops of the strips
Find area of strips (trapeziums) using Area = ½(a + b)h
Add the areas
How do I know if my answer is an underestimate or an overestimate?
A common exam question is to ask if your estimate of the area is an underestimate or an overestimate
To answer this, simply look at the straight lines joining the tops of your strips
If the straight lines are below the curve, it is an underestimate
If the straight lines are above the curve, it is an overestimate
In your exam, the lines will all be below or all be above the curve- though it may be difficult to tell which for some strips
Examiner Tips and Tricks
This is particularly useful when working with speed-time and distance-time graphs if they are curves and not straight lines.
Worked Example
The graph below shows for
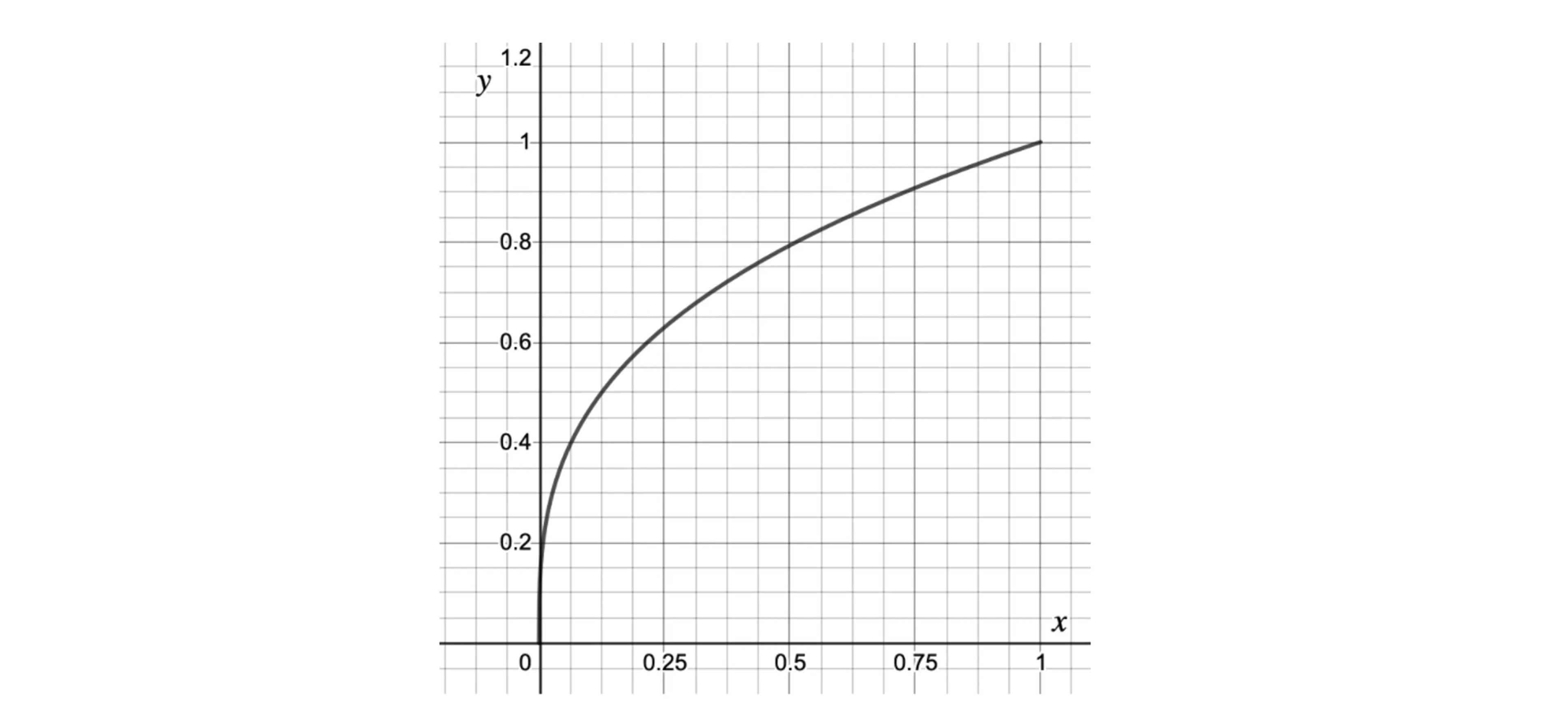
Find an estimate for the area between the curve, the axis and the line
. Use four strips of equal width.
Split the area into four strips using the width of 0.25 for each one
Find the coordinate at the end of each strip by reading the value from the graph or substituting the
coordinate into

Find the area of each strip by using the formula for the area of a trapezium

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?