Frequency Trees (Edexcel GCSE Maths)

Frequency Trees

What are frequency trees?

• Frequency trees show the frequencies associated with two properties of a set of data

• They are usually used when each property only has two possible outcomes

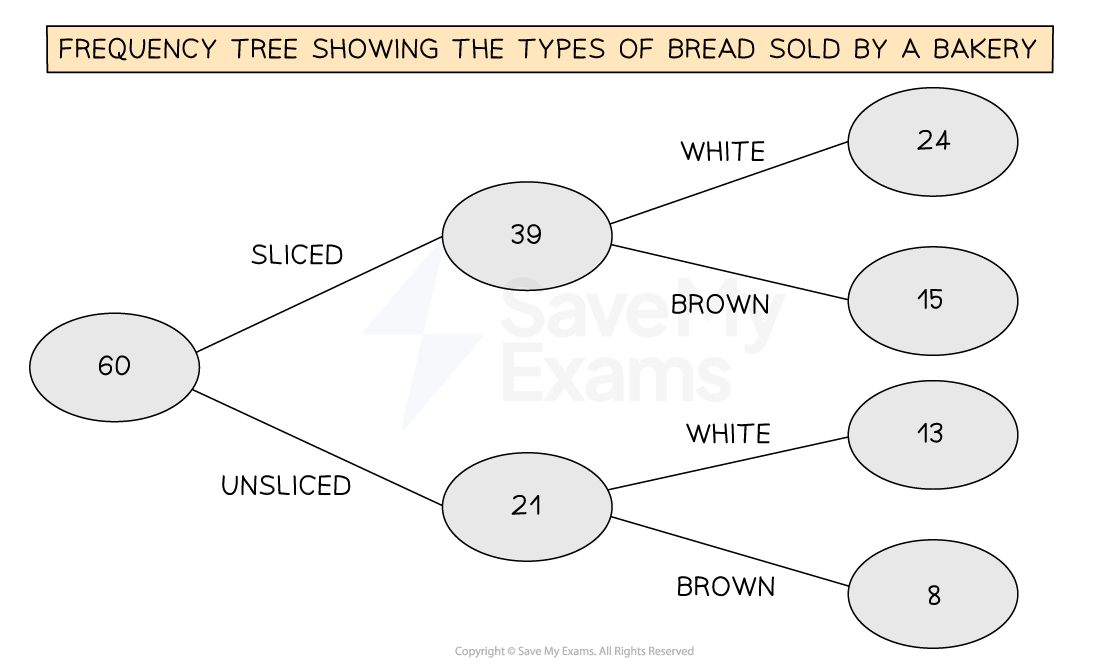
  • For example the types of bread sold by a bakery in a day
    

    • The first property could be if the bread is sliced or unsliced

    • The second property could be if the bread is white or brown

  • A frequency tree shows the frequency for each combination

    • e.g how many sliced, white loaves of bread were sold

• The total frequency appears in a 'bubble' at the start of a frequency tree

  • The first set of branches then break this down by the two outcomes for the first property

  • The second set of branches then further breaks down each of those frequencies

• It does not matter which set of branches shows which property

• It is possible to have three, or more, properties on a frequency tree by adding more sets of branches

  • However these would quickly become large and cumbersome

• For situations with more than two options for a property, two-way tables are more useful

  • For example if the bread in the bakery could brown, white, or seeded

How do I draw a frequency tree?

• If drawing a frequency tree from scratch
  

  • Identify the two properties

  • Decide which property to put on the first set of branches and which to put on the second set of branches

  • Remember to include a 'bubble' at the start for the total frequency and a 'bubble' at the end of each branch

• Double check that the values at the ends of the branches, sum to the 'bubble' that they are connected to

How do I complete a frequency tree?

• Often in an exam there will be a partially completed frequency tree

• Check for any values in the question that you can use to fill in gaps

  • e.g. "A total of 100 people"

• Remember that the values at the ends of the branches, sum to the 'bubble' that they are connected to
  

  • This should allow you to fill in any gaps that aren't revealed by the information in the question

How do I find probabilities from a frequency tree?

• Similar to finding probabilities from two-way tables, you need to select the appropriate numbers from the diagram

• It can help to rephrase the question to use AND & OR statements
  

  • e.g.  The probability of selecting a loaf of sliced white bread is P("sliced AND white")

• Use the branches to help select the values you need to write down the probability
  

  • For "sliced AND white" this would be the along the branch saying 'sliced' on the first property and 'white' on the second

    • The value in the bubble at the end of the required branch(es) would be the numerator

  • The denominator will be the total of the group we are choosing from

    • This could be the whole group - the total frequency at the start of the diagram

    • Or if we are finding a probability from just sliced loaves, it would be the frequency in the bubble at the end of the 'sliced' branch

• You may need to add together values

  • e.g. To find the total number of white loaves of bread sold, sum together the sliced white loaves and the unsliced white loaves