Surface Area (Edexcel GCSE Maths) : Revision Note
Did this video help you?
Surface Area
What is surface area?
The surface area of a 3D object is the sum of the areas of all the faces that make up the shape
Area is a 2D idea being applied into a 3D situation
A face is one of the flat or curved surfaces that make up a 3D object
How do I find the surface area of cubes, cuboids, pyramids, and prisms?
In cubes, cuboids, polygonal-based pyramids, and polygonal-based prisms (ie. pyramids and prisms whose bases have straight sides), all the faces are flat
The surface area is found by
calculating the area of each individual flat face
adding these areas together
When calculating surface area, it can be helpful to draw a 2D net for the 3D shape in question
For example, consider a square-based pyramid where the top of the pyramid is directly above the centre of the base
Its net will consist of a square base and four identical isosceles triangular faces
Calculate the area of a square and the area of each triangle then add them together

How do I find the surface area of a cylinder?
A cylinder has two flat surfaces (the top and the base) and one curved surface
The net of a cylinder consists of two circles and a rectangle

The curved surface area (which is a rectangle) of a cylinder, A, with base radius, r, and height, h, is therefore given by
This is the circumference of the circle, multiplied by the height
This formula is not given to you in the exam
The total surface area of a cylinder, ATotal, can be found using the formula
This is the area of the curved surface (a rectangle), plus two circles of radius r
This formula is not given to you in the exam
How do I find the surface area of a cone?
A cone has one flat surface (the base) and one curved surface
The net of a cone, with radius, r, perpendicular height, h, and sloping edge, (slant height), l, consists of
A circular base
A sector with radius, l, and an arc length equal to the circumference of the base

The curved surface area of a cone, A, with radius, r, perpendicular height, h, and sloping edge, l, can be found using the formula
This formula is given to you in the exam if it is needed
The total surface area of a cone, ATotal, can be found using the formula
This formula is not given to you in the exam
It is just the curved surface area formula above, plus the area of a circle
How do I find the surface area of a sphere?
A sphere has a single curved surface
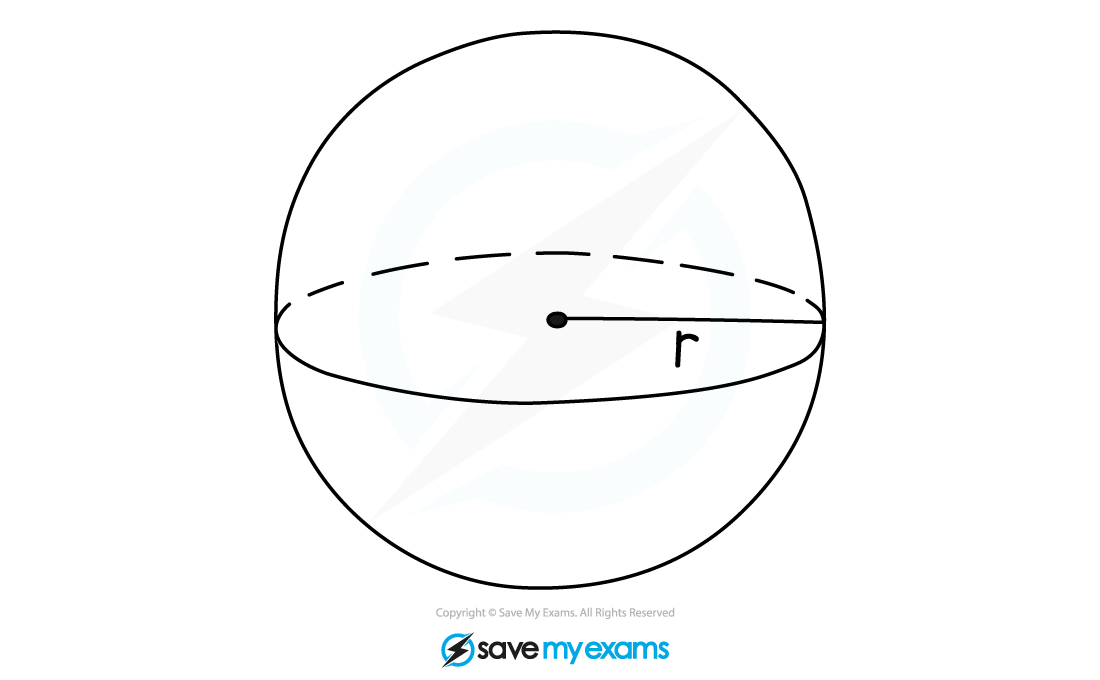
The surface area of a sphere, A, with radius, r, can be found using the formula
This formula is given to you in the exam if it is needed
Examiner Tips and Tricks
Read the question carefully, you may need to add additional areas, e.g. a base
Make you are confident in calculating the areas of rectangles, circles and triangles
Worked Example
Find the surface area of the cuboid shown below.

Find the area of the face at the front
2 cm × 10 cm = 20 cm2
Find the area of the face at the side
2 cm × 15 cm = 30 cm2
Find the area of the face at the top
10 cm × 15 cm = 150 cm2
There are two of each face
Add together the areas of all 6 faces
20 + 20 + 30 + 30 + 150 + 150 = 400
400 cm2

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

