GCSEMathsEdexcelFoundationRevision NotesGeometry & MeasuresTransformationsEnlargements

Enlargements (Edexcel GCSE Maths)

Revision Note

Test yourself
Dan Finlay

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Edexcel Maths: FoundationEdexcel Maths: Higher

Did this video help you?

Enlargements

What is an enlargement?

  • An enlargement changes the size and position of a shape

  • The length of each side of the shape is multiplied by a scale factor

    • If the scale factor is greater than 1 then the enlarged image will be bigger than the original object

    • If the scale factor is less than 1 then the enlarged image will be smaller than the original object

  • The centre of enlargement determines the position of the enlarged image

    • If the scale factor is greater than 1 then the enlarged image will be further away from the centre of enlargement

    • If the scale factor is less than 1 then the enlarged image will be closer to the centre of enlargement

How do I enlarge a shape?

  • STEP 1

    Pick a vertex of the shape and count the horizontal and vertical distances from the centre of enlargement

  • STEP 2
    Multiply both the horizontal and vertical distances by the given scale factor

  • STEP 3
    Start at the centre of enlargement and measure the new distances to find the enlarged vertex

  • STEP 4
    Repeat the steps for the other vertices

    • You might be able to draw the enlarged shape from the first vertex by multiplying the original lengths by the scale factor

      • This can be done quickly if the shape is made up of vertical and horizontal lines

  • STEP 5
    Connect the vertices on the enlarged image and label it

How do I describe an enlargement?

  • To describe an enlargement, you must:

    • State that the transformation is an enlargement

    • State the scale factor

    • Give the coordinates of the centre of enlargement

  • To find the scale factor:

    • Pick a side of the original shape

    • Identify the corresponding side on the enlarged image

    • Divide the length of the enlarged side by the length of the original side

  • To find the centre of enlargement:

    • Pick a vertex of the original shape

    • Identify the corresponding vertex on the enlarged image

    • Draw a line going through these two vertices

    • Repeat this for the other vertices of the original shape

    • These lines will intersect at the centre of enlargement

How do I reverse an enlargement?

  • If a shape has been enlarged, you can perform a single transformation to return the shape to its original size and position

  • An enlargement can be reversed by multiplying the enlarged shape by the reciprocal of the original scale factor

    • The centre of enlargement is the same

  • For a shape enlarged by a scale factor of 3 with centre of enlargement (-1, 6)

    • The reverse transformation is

      • an enlargement of scale factor 1 third

      • with centre of enlargement (-1, 6)

Examiner Tips and Tricks

  • To check that you have enlarged a shape correctly:

    • Draw lines going from the centre of enlargement to each of the vertices of the original shape

    • Extend these lines

    • The lines should go through the corresponding vertices of the enlarged image

Worked Example

(a) On the grid below enlarge shape C using scale factor 2 and centre of enlargement (2, 1).

Label your enlarged shape C'.

Enlargement-Q1, IGCSE & GCSE Maths revision notes

Start by marking on the centre of enlargement (CoE).
Count the number of squares in both a horizontal and vertical direction to go from the CoE to one of the vertices on the original object, this is 2 to the right and 3 up in this example.
As the scale factor is 2, multiply these distances by 2, so they become 4 to the right and 6 up.
Count these new distances from the CoE to the corresponding point on the enlarged image and mark it on.
Draw a line through the CoE and the pair of corresponding points, they should line up in a straight line. 

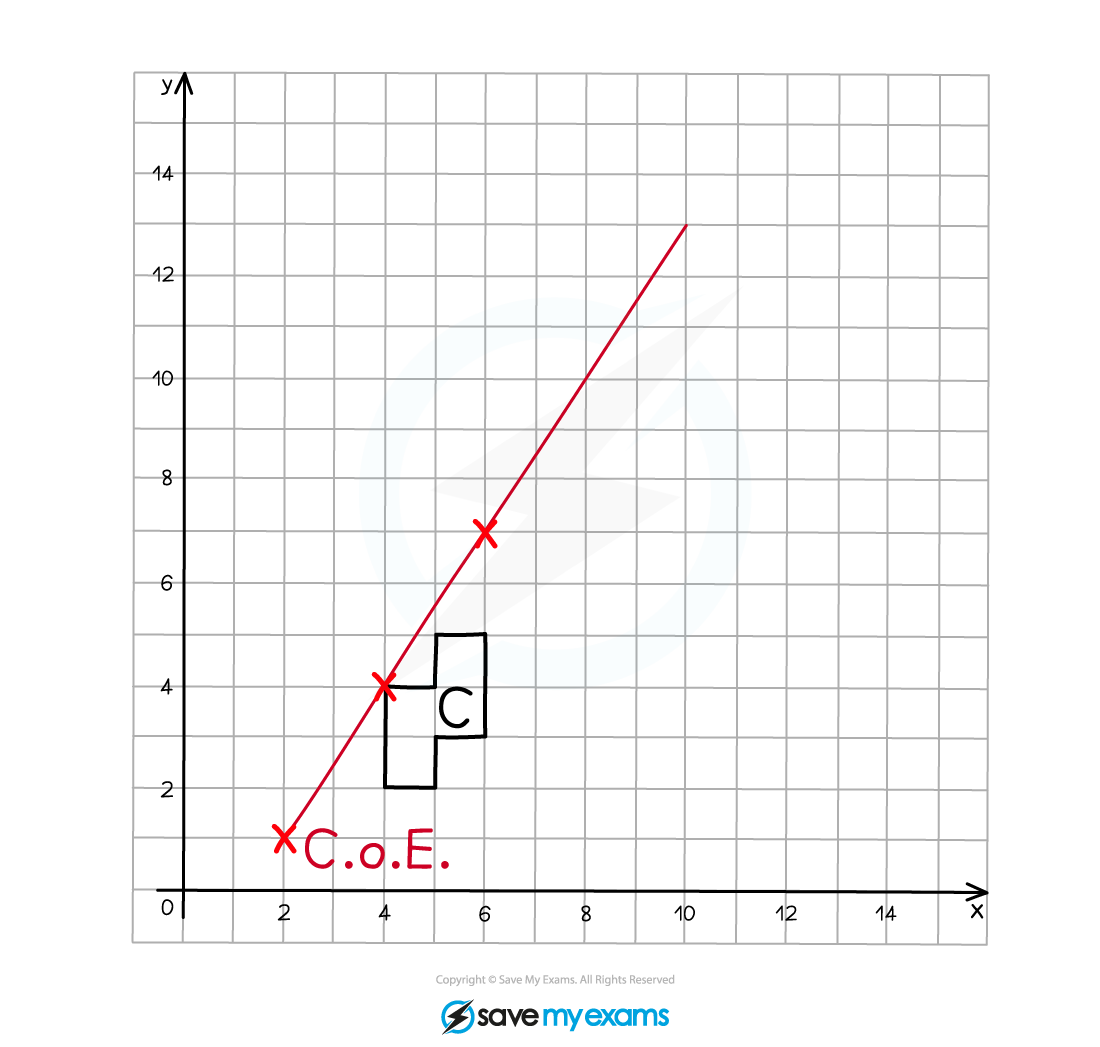
Enlargement-Q1-working, IGCSE & GCSE Maths revision notes

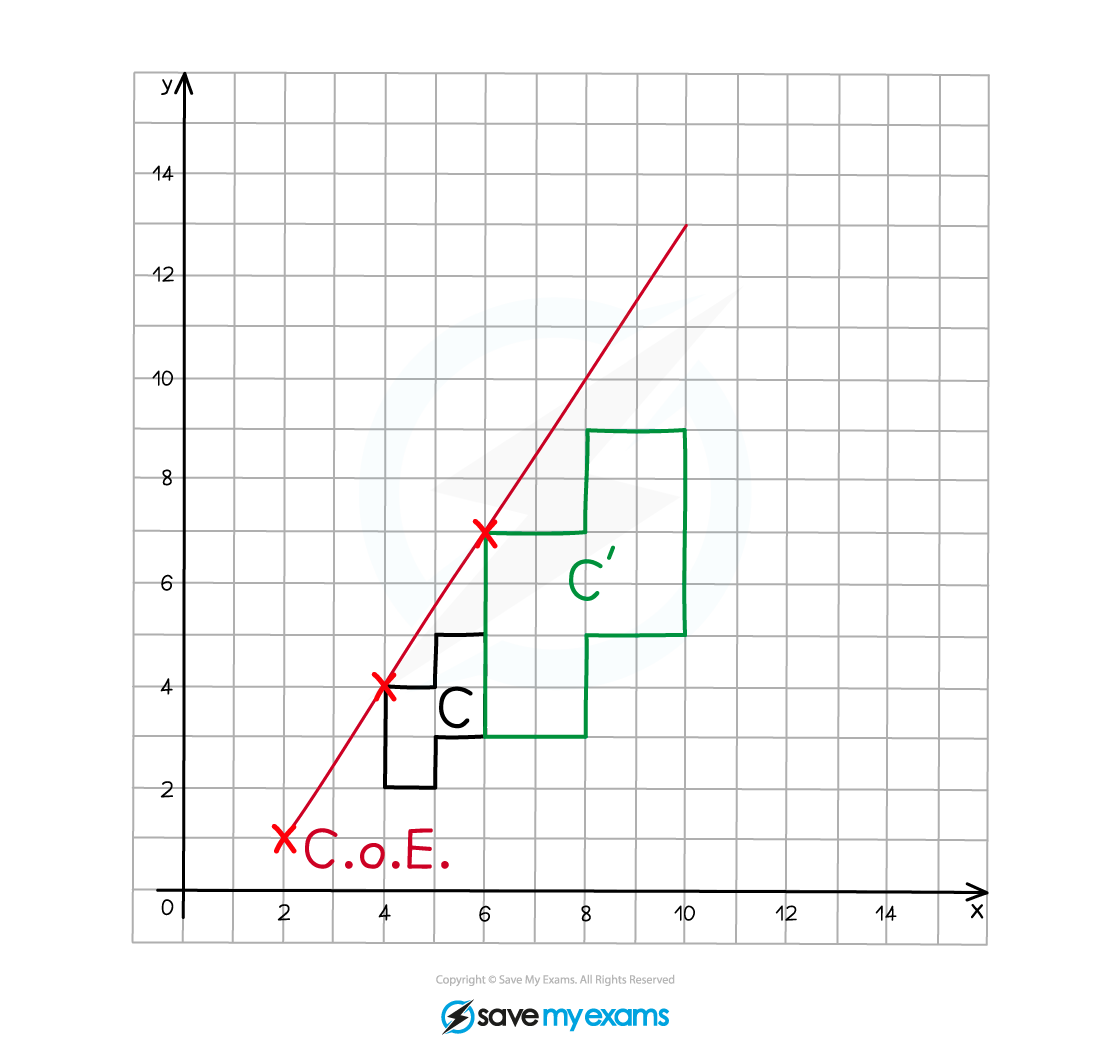
Repeat this process for each of the vertices on the original object (or at least 2).
Join adjacent vertices on the enlarged image as you go.
Label the enlarged image C'.

Enlargement-Q1-Final-Answer, IGCSE & GCSE Maths revision notes

(b) Describe fully the single transformation that creates shape B from shape A.

Enlargement-Q2, IGCSE & GCSE Maths revision notes

We can see that the image is larger than the original object, therefore it must be an enlargement.
As the enlarged image is bigger than the original object, the scale factor must be greater than 1.
Compare two corresponding edges on the object and the image to find the scale factor.

The height of the original "H" is 3 squares
The height of the enlarged "H" is 9 squares

therefore Scale space Factor space equals 9 over 3 equals 3

Draw a straight line through the CoE and a pair of corresponding points on the original object and the enlarged image.
Repeat this step for as many vertices as you feel you need to so you can confidently locate the CoE.
Do this for all pairs of vertices to be sure!
The point of intersection of the lines is the CoE.

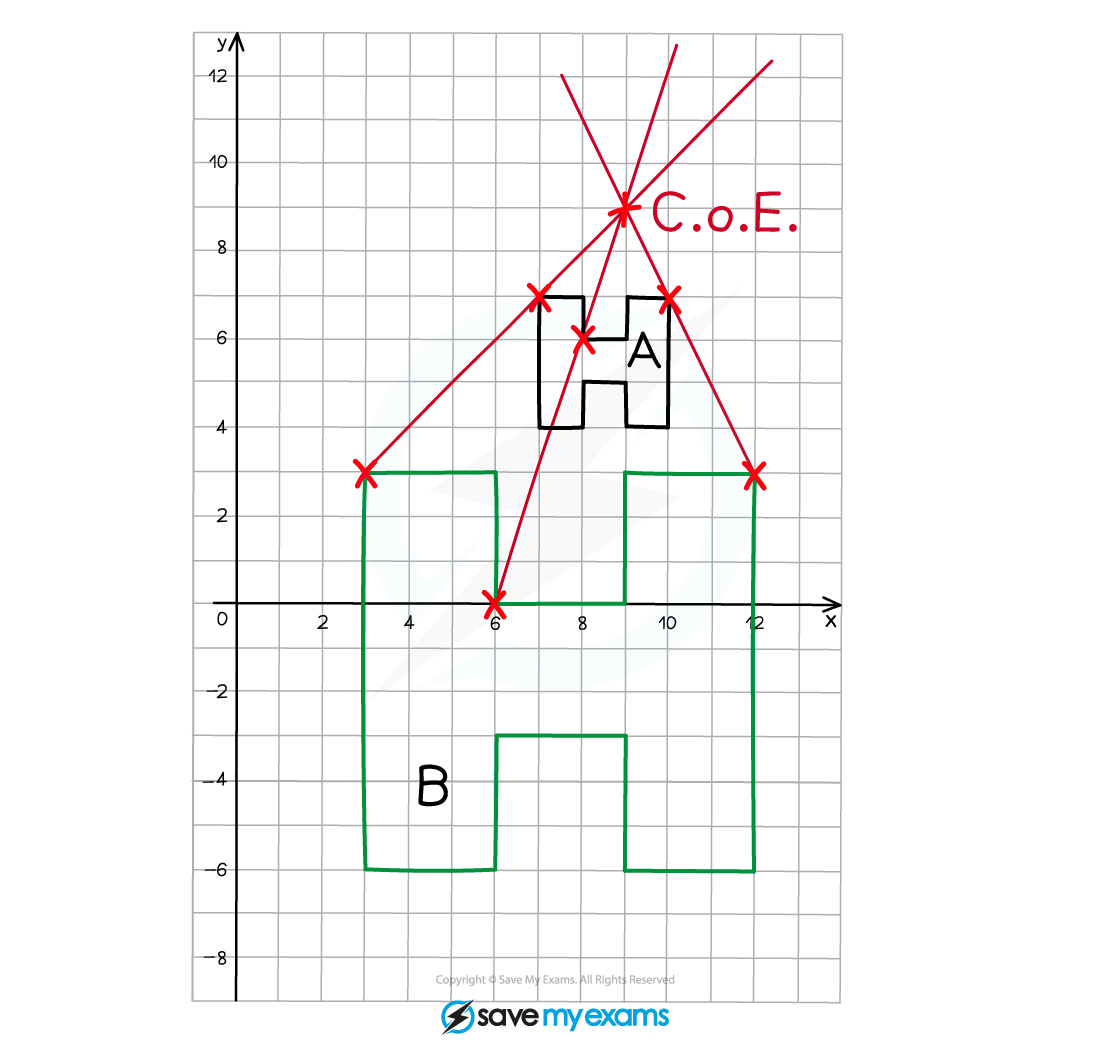
Enlargement-Q2-Working, IGCSE & GCSE Maths revision notes

Shape A has been enlarged using a scale factor of 3 and a centre of enlargement (9, 9) to create shape B

Fractional Enlargements

How do I enlarge a shape with a fractional scale factor?

  • You follow the same steps as for other enlargements

  • The only differences will be the enlarged shape's size and position

    • The enlarged shape will be smaller than the original

      • These are still called enlargements even though the shape gets smaller

    • The enlarged shape will be closer to the centre of enlargement than the original 

How do I describe an enlargement with a fractional scale factor?

  • To describe an enlargement, must: 

    • State that the transformation is an enlargement

    • State the scale factor

      • This will be a fraction

    • Give the coordinates of the centre of enlargement

  • To find the scale factor:

    • Pick a side of the original shape

    • Identify the corresponding side on the enlarged image

      • This should be smaller 

    • Divide the length of the enlarged side by the length of the original side

How do I reverse a fractional enlargement?

  • If a shape has undergone a fractional enlargement, you can perform a single transformation to return the shape to its original size and position

  • An enlargement can be reversed by multiplying the enlarged shape by the reciprocal of the original scale factor

    • the centre of enlargement is the same

  • For a shape enlarged by a scale factor of 1 half with centre of enlargement (0, 5)

    • The reverse transformation is

      • an enlargement of scale factor 2

      • with centre of enlargement (0, 5)

Examiner Tips and Tricks

  • Multiplying by the fraction 1 over n is the same as dividing by n

    • 6 cross times 1 half is the same as 6 divided by 2

    • This can make the calculations quicker on the non-calculator paper

Worked Example

(a) On the grid below enlarge shape C using scale factor 1 half and centre of enlargement (4, 2).

Write down the four vertices of your enlarged shape.

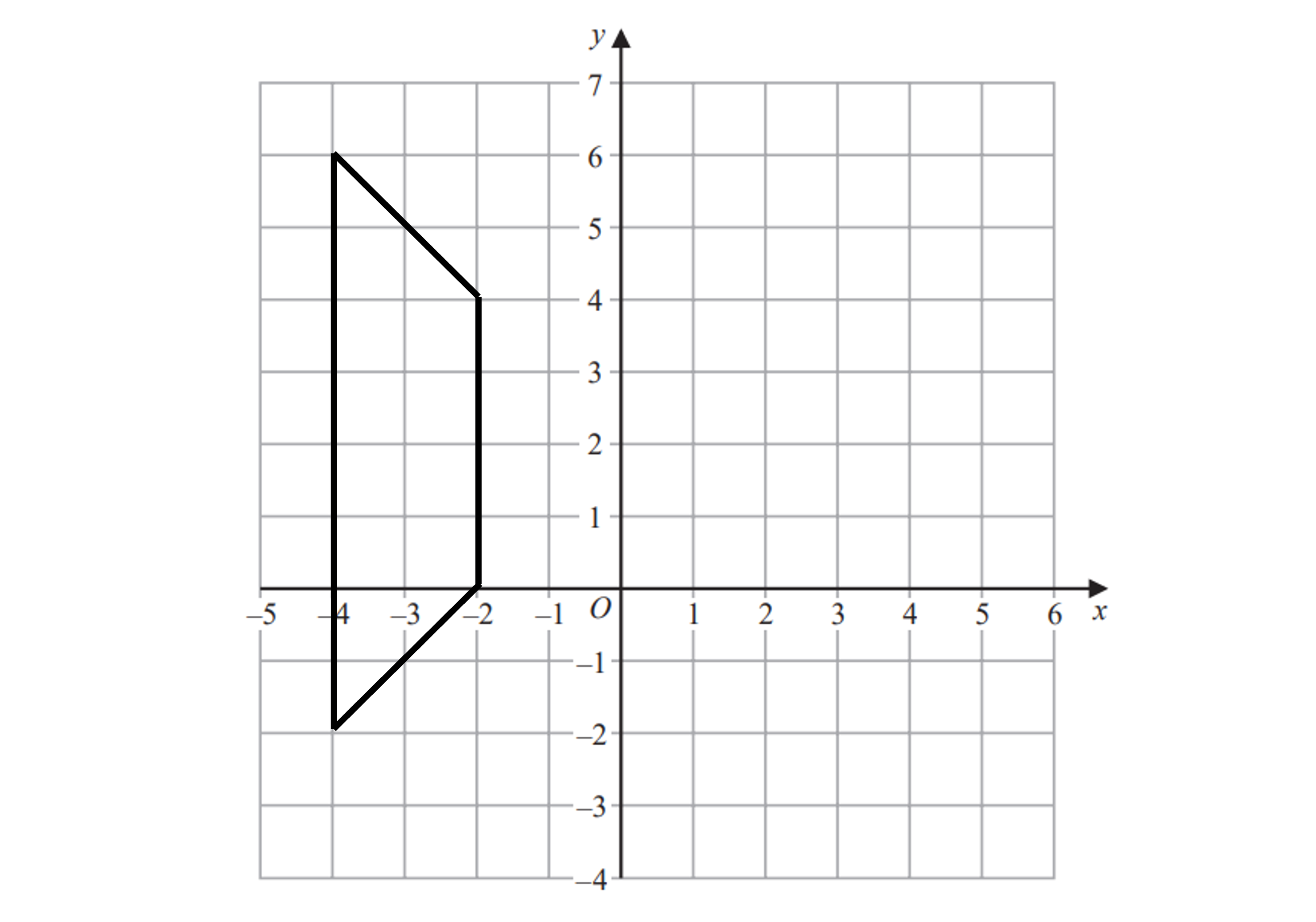
cie-igcse-core-fractional-enlargements-rn-we-a1-image

Mark the centre of enlargement at (4, 2)
Count the number of squares horizontally and vertically to any vertex - we've chosen the vertex at (-2, 4)

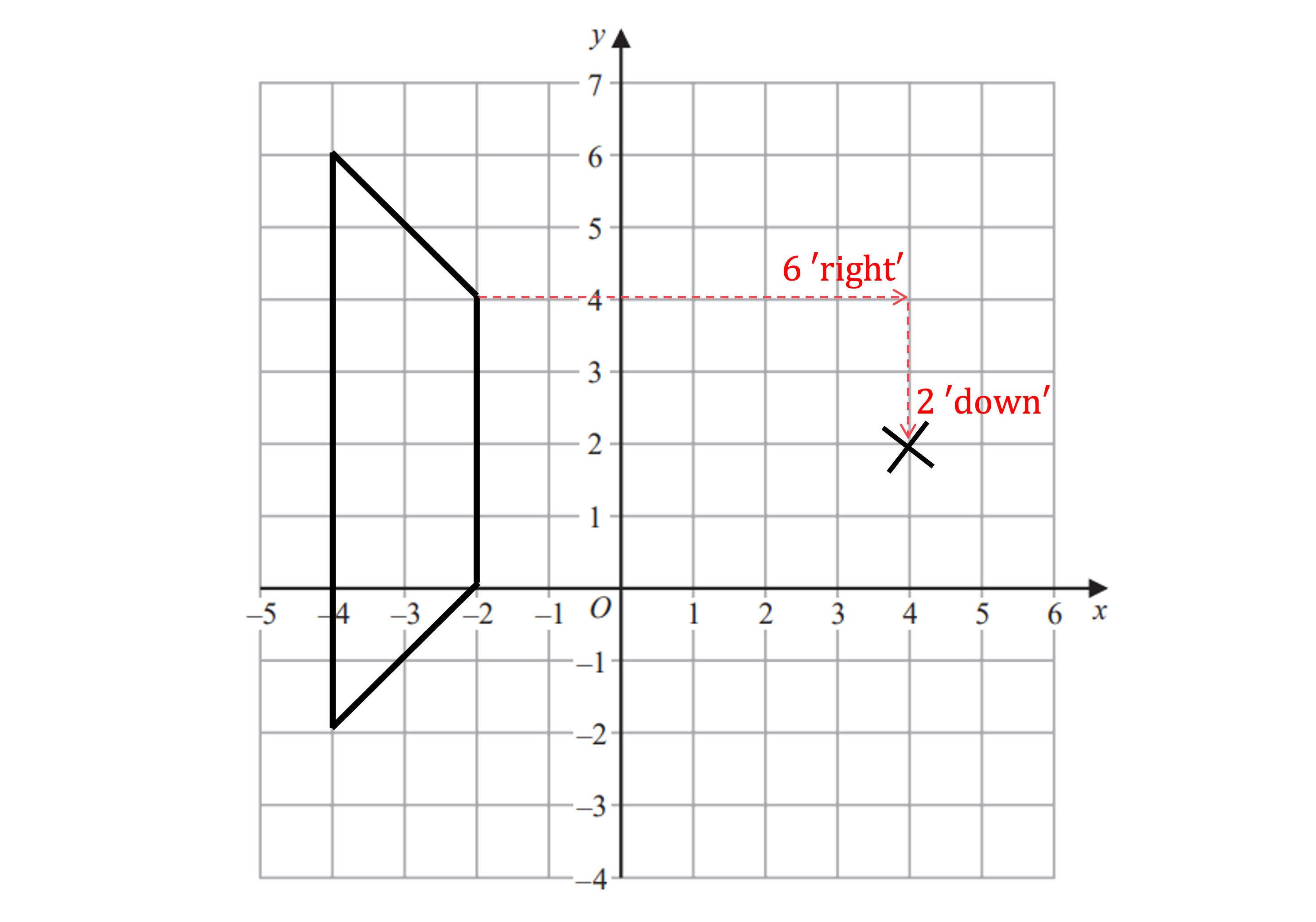
cie-igcse-core-fractional-enlargements-rn-we-a2-image

Multiply these distance by the scale factor, 1 half

6 'right cross times 1 half equals 3 'right'

2 'down' cross times 1 half equals 1 'down'

Count these new distances (which should be smaller than the originals) from the CoE to find the corresponding point on the new image and mark it on

Repeat as required and draw lines through corresponding vertices and the CoE as a check

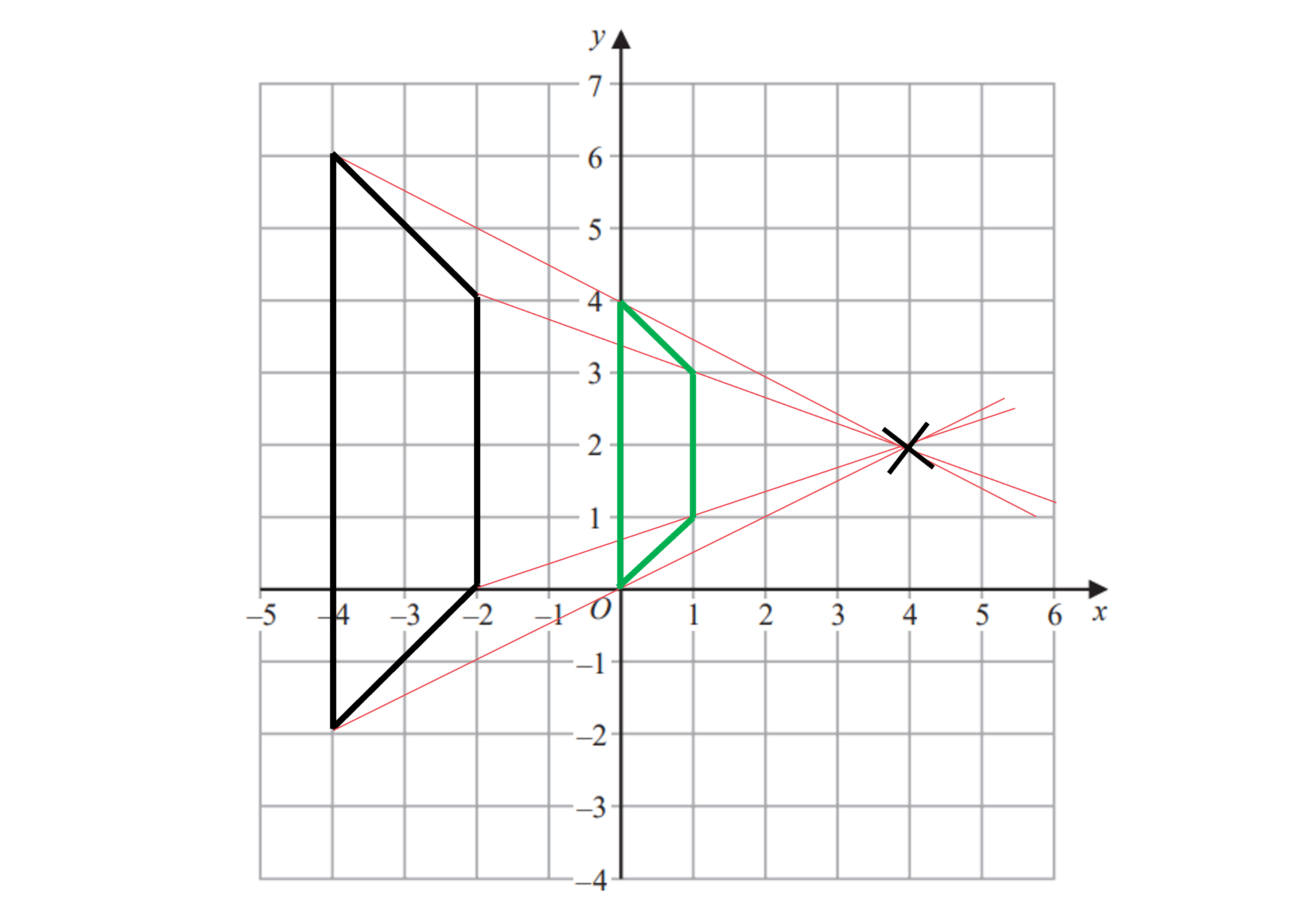
cie-igcse-core-fractional-enlargements-rn-we-a3-image

The four vertices of the enlarged shape are (0, 0), (0, 4),  (1, 3) and (1, 1)

Use a logical order, working your way round the shape slowly, to ensure you do miss any vertices out.

(b) Describe fully the single transformation that creates shape B from shape A.

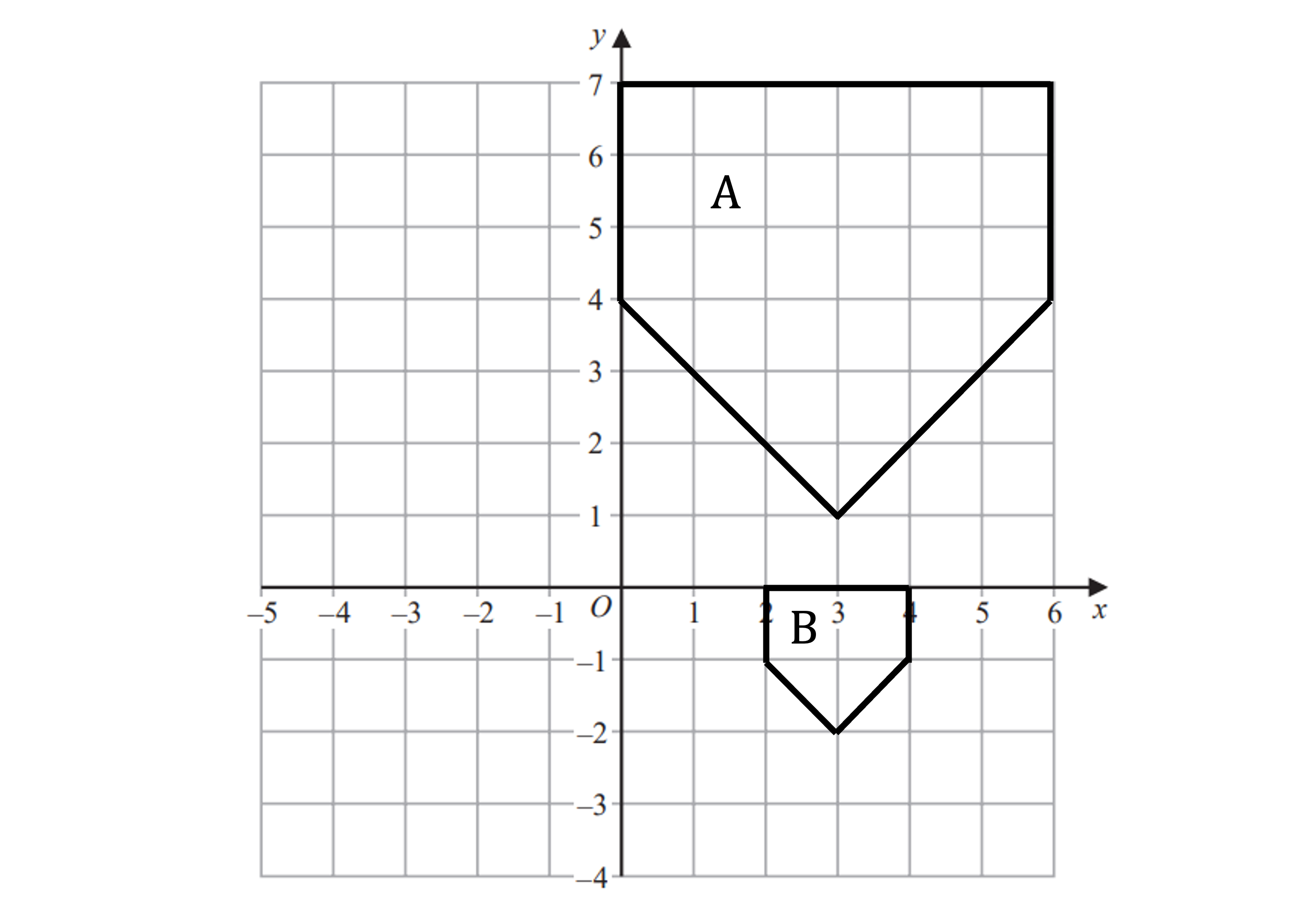
cie-igcse-core-fractional-enlargements-rn-we-b1-image

We can see the image is smaller than the original so it is a fractional enlargement
Compare two corresponding edges to find the scale factor - we've used the top edge

scale factor = fraction numerator new space edge over denominator old space edge end fraction equals 2 over 6 equals 1 third

Draw straight lines through corresponding vertices on the original shape
Repeat this 3-4 times and you should find the lines intersect at the same point
This point will be the CoE

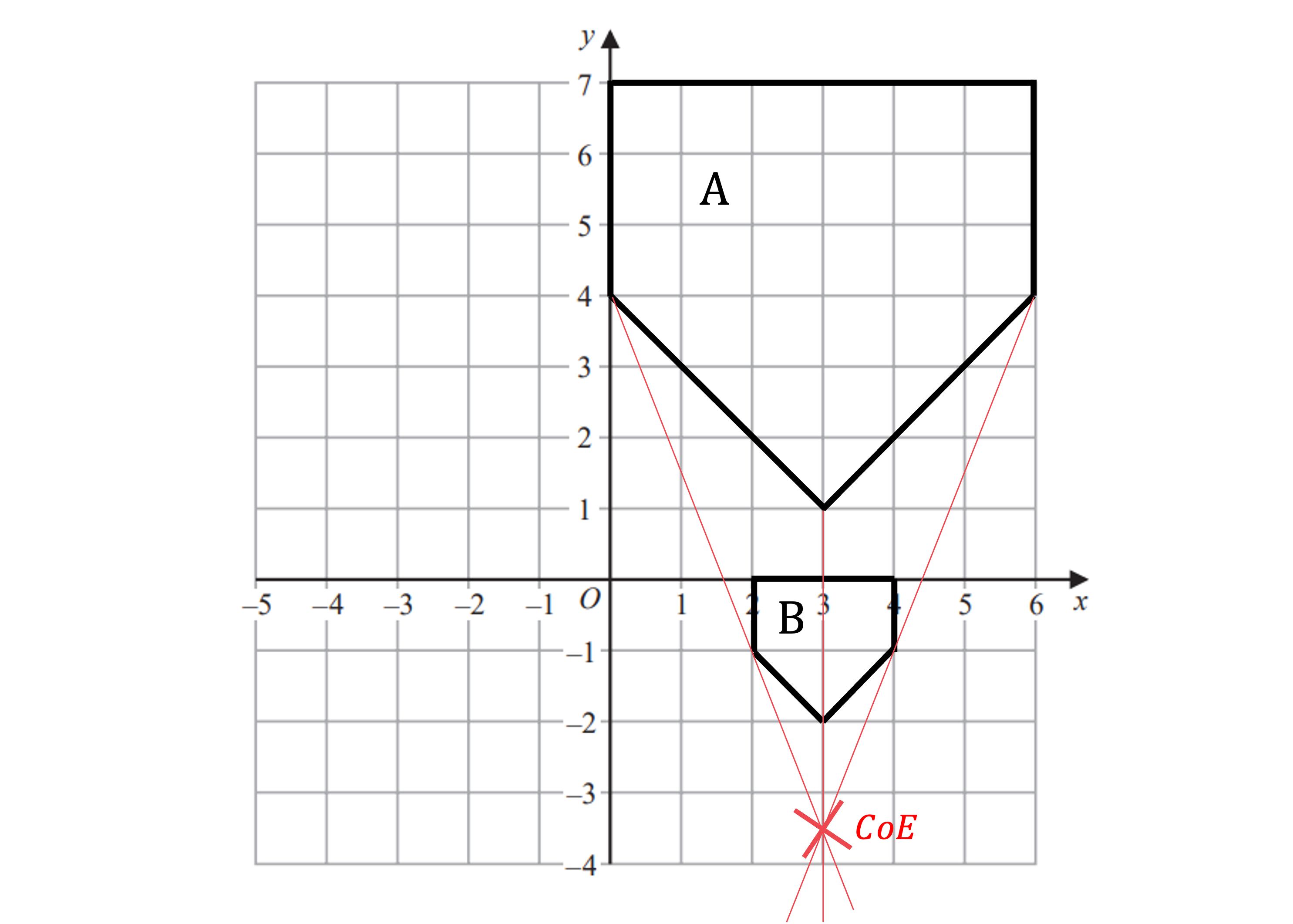
cie-igcse-core-fractional-enlargements-rn-we-b2-image

Shape A has been enlarged using a scale factor of 1 thirdand a centre of enlargement (3, -3.5) to create shape B

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:RotationsNext:Basic Probability
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Lucy Kirkham

    Author: Lucy Kirkham

    Expertise: Head of STEM

    Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels.Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all.