Tree Diagrams

How do I draw a tree diagram?

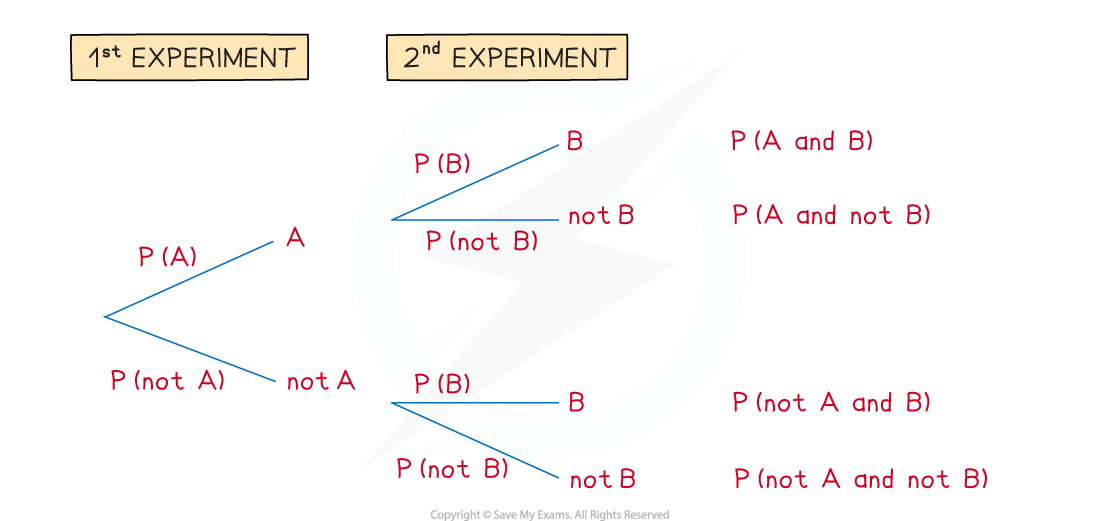
Tree diagrams can be used for repeated experiments with two outcomes
- The 1st experiment has outcome A or not A
- The 2nd experiment has outcome B or not B
Read the tree diagram from left to right along its branches
- For example, the top branches give A followed by B
  - This is called A and B

How to set up a tree diagram for two experiments each with two possible outcomes

How do I find probabilities from tree diagrams?

Write the probabilities on each branch
- Remember that P(not A) = 1 - P(A)
  - Probabilities on each pair of branches add to 1
Multiply along the branches from left to right
- This gives P(1st outcome and 2nd outcome)
Add between the separate cases
- For example
  - P(AA or BB) = P(AA) + P(BB)
The probabilities of all possible cases add to 1
If asked to find the probability of at least one outcome, it is quicker to do 1 - P(none)

Examiner Tip

When multiplying along branches with fractions, don't cancel fractions in your working - having the same denominator makes them easier to add together!

Worked example

A worker drives through two sets of traffic lights on their way to work.
Each set of traffic lights has only two options: green or red.
The probability of the first set of traffic lights being on green is $\frac{5}{7}$ .
The probability of the second set of traffic lights being on green is $\frac{8}{9}$ .

(a)

Draw and label a tree diagram. Show the probabilities of every possible outcome.

Work out the probabilities of each set of traffic lights being on red, R
Use P(red) = 1 - P(green)

$P (1^{st} R) = 1 - P (1^{st} G) = 1 - \frac{5}{7} = \frac{2}{7}$
$P (2^{nd} R) = 1 - P (2^{nd} G) = 1 - \frac{8}{9} = \frac{1}{9}$

Draw the branches (with a label of G or R on the ends)
Write the probabilities above each branch
Calculate probabilities of each outcome by multiplying along the branches from left to right

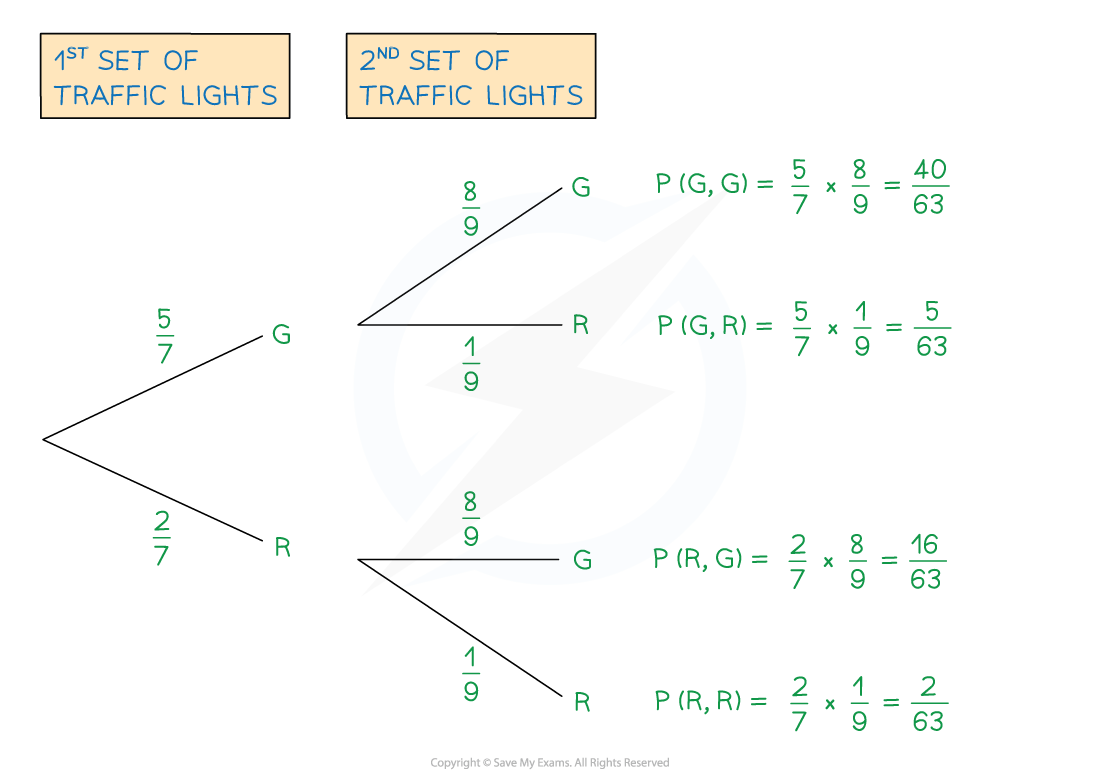
A tree diagram showing different outcomes at traffic lights

(b)

Find the probability that both sets of traffic lights are on red.

This is the answer for P(R, R) from the tree diagram

$\frac{2}{63}$

(c)

Find the probability that at least one set of traffic lights are on red.

This means the 1st is green and the 2nd is red
Or the 1st is red and the 2nd is green
Or the 1st is red and the 2nd is red ('at least one' could mean both)
Add between the separate cases

$P (at least one R) = P (G, R) + P (R, G) + P (R, R) = \frac{5}{63} + \frac{16}{63} + \frac{2}{63} = \frac{23}{63}$

$\frac{23}{63}$

Alternative Method
At least one red means all the possible cases shown except two greens
So P(at least 1 red) = 1 - P(two greens)

$1 - P (G, G) = 1 - \frac{40}{63} = \frac{23}{63}$

$\frac{23}{63}$

Tree Diagrams (Edexcel GCSE Maths: Foundation)

Revision Note

Tree Diagrams

How do I draw a tree diagram?

How do I find probabilities from tree diagrams?

Examiner Tip

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Mark