GCSEMaths: FoundationEdexcelRevision NotesProbabilitySimple Probability DiagramsFrequency Trees

Frequency Trees (Edexcel GCSE Maths: Foundation)

Revision Note

Test yourself
Jamie W

Author

Jamie W

Last updated

Frequency Trees

What are frequency trees?

  • Frequency trees show the frequencies associated with two properties of a set of data
  • They are usually used when each property only has two possible outcomes
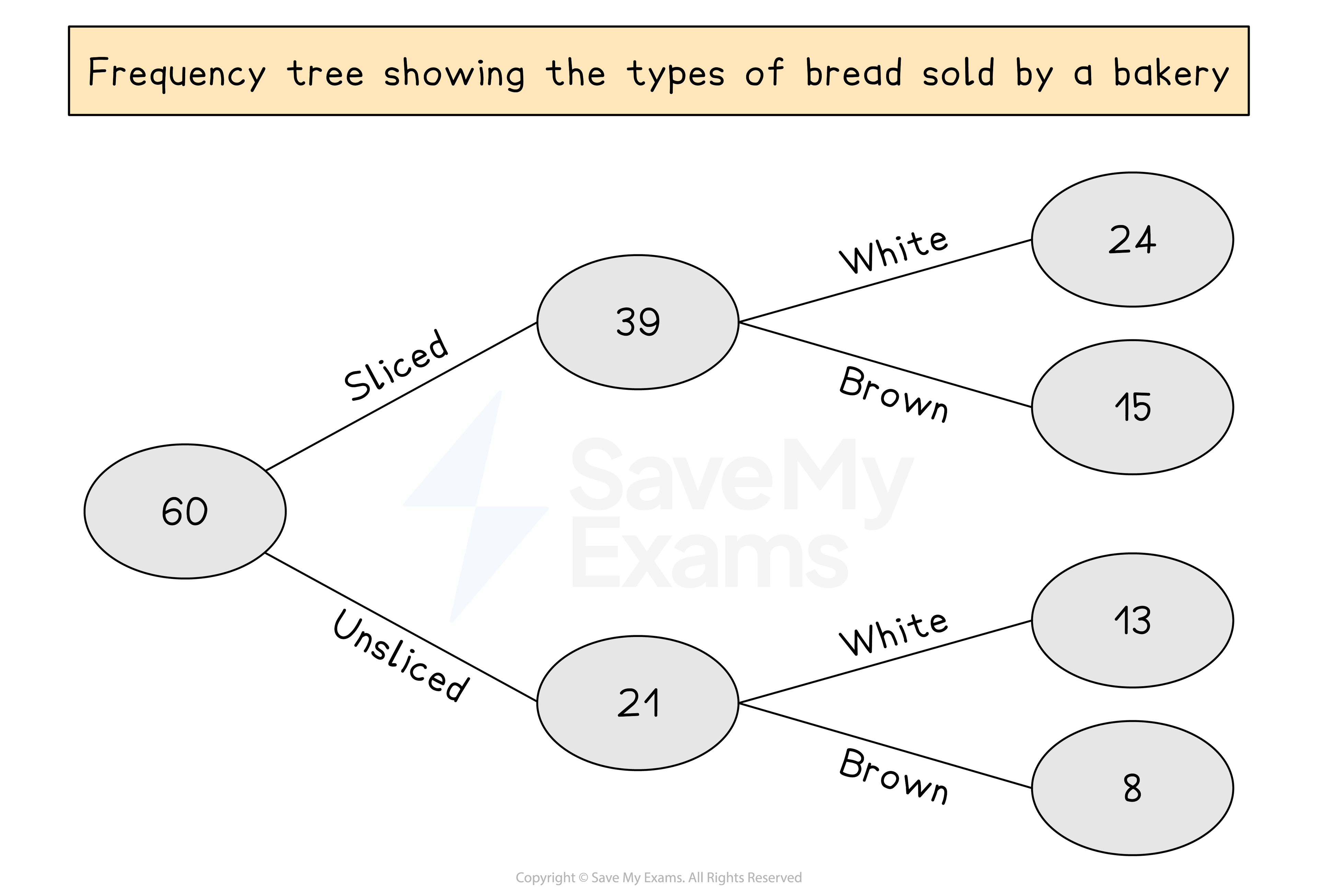
    • For example the types of bread sold by a bakery in a day
      • The first property could be if the bread is sliced or unsliced
      • The second property could be if the bread is white or brown
    • A frequency tree shows the frequency for each combination
      • e.g how many sliced, white loaves of bread were sold
  • The total frequency appears in a 'bubble' at the start of a frequency tree
    • The first set of branches then break this down by the two outcomes for the first property
    • The second set of branches then further breaks down each of those frequencies
  • It does not matter which set of branches shows which property
  • It is possible to have three, or more, properties on a frequency tree by adding more sets of branches
    • However these would quickly become large and cumbersome
  • For situations with more than two options for a property, two-way tables are more useful
    • For example if the bread in the bakery could brown, white, or seeded

Frequency tree showing the types of bread sold by a bakery, broken down first by sliced or unsliced, and then by brown or white

How do I draw a frequency tree?

  • If drawing a frequency tree from scratch
    • Identify the two properties
    • Decide which property to put on the first set of branches and which to put on the second set of branches
    • Remember to include a 'bubble' at the start for the total frequency and a 'bubble' at the end of each branch
  • Double check that the values at the ends of the branches, sum to the 'bubble' that they are connected to

How do I complete a frequency tree?

  • Often in an exam there will be a partially completed frequency tree
  • Check for any values in the question that you can use to fill in gaps
    • e.g. "A total of 100 people"
  • Remember that the values at the ends of the branches, sum to the 'bubble' that they are connected to
    • This should allow you to fill in any gaps that aren't revealed by the information in the question

How do I find probabilities from a frequency tree?

  • Similar to finding probabilities from two-way tables, you need to select the appropriate numbers from the diagram
  • It can help to rephrase the question to use AND & OR statements
    • e.g.  The probability of selecting a loaf of sliced white bread is P("sliced AND white")
  • Use the branches to help select the values you need to write down the probability
    • For "sliced AND white" this would be the along the branch saying 'sliced' on the first property and 'white' on the second
      • The value in the bubble at the end of the required branch(es) would be the numerator
    • The denominator will be the total of the group we are choosing from
      • This could be the whole group - the total frequency at the start of the diagram
      • Or if we are finding a probability from just sliced loaves, it would be the frequency in the bubble at the end of the 'sliced' branch
  • You may need to add together values
    • e.g. To find the total number of white loaves of bread sold, sum together the sliced white loaves and the unsliced white loaves

Examiner Tip

  • Double check that the values at the ends of the tree add up to the starting value
  • Some of the frequencies may be given as fractions or percentages of others
    • e.g.  65% of the loaves of bread sold were sliced

Worked example

80 students are learning how to DJ. There are two courses; scratch mixing, and beat mixing.
60% of the students are studying scratch mixing, the rest are studying beat mixing.
Of those studying scratch mixing, 15 are female.
Of those studying beat mixing, 12 are male.

(a)
Use the information above to complete the frequency tree.

5-2-4-frequency-tree-we-question

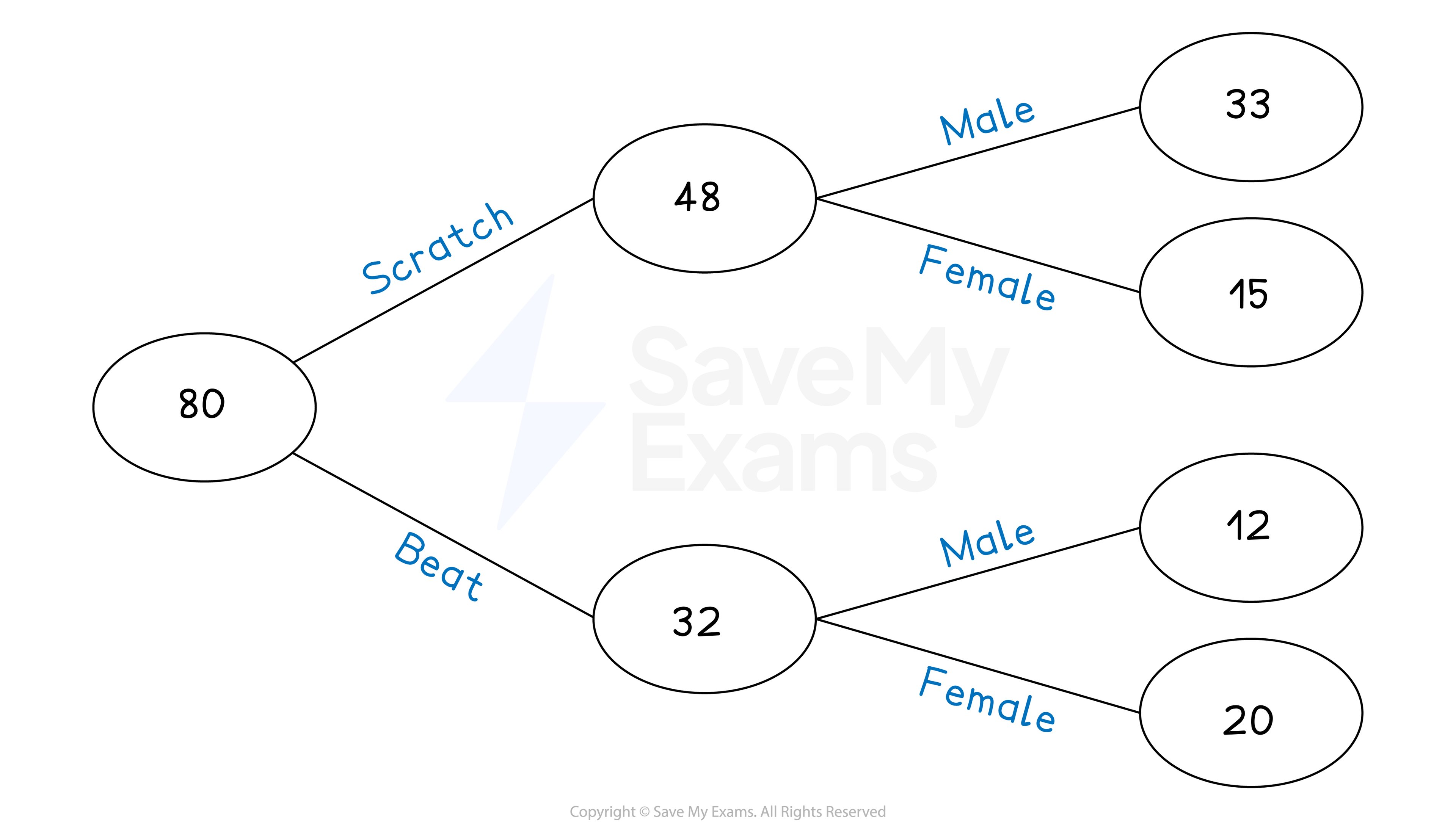
Start with the total frequency bubble at the start of the frequency tree - 80.
Work out 60% of 80 to find the frequency for scratch mixing.

table row cell 10 percent sign space of space 80 space end cell equals cell 80 divided by 10 equals 8 end cell row cell 60 percent sign space of space 80 space end cell equals cell space 8 cross times 6 equals 48 end cell end table

Work your way through the rest of the tree.

beat: 80 space minus space 48 space equals 32

We are given that 15 of those studying scratch mixing are female and that 12 of those studying beat mixing are male.

scratch and female: 48 space minus space 15 space equals space 33
beat and female: 32 minus 12 equals 20

Now we have all the values, we can complete the frequency tree.


5-2-4-frequency-tree-we-solutionCheck the bubble totals:  48 + 32 = 80, 33 + 15 + 12 + 20 = 80

(b)
(i)
A student is chosen at random.  Find the probability that the student is a male studying beat mixing.

(ii)
A student studying scratch mixing is chosen at random.  Find the probability that the they are female.

(i)
Rephrasing this is P("male AND beat mixing").
The numerator will be the value in the bubble at the end of the branches "beat mixing" and "male" (12).
We are choosing from all of the students, so the denominator will be the total frequency (80).

bold P bold left parenthesis bold male bold space bold practising bold space bold beat bold space bold mixing bold right parenthesis bold equals bold 12 over bold 80 stretchy left parenthesis equals 3 over 20 stretchy right parenthesis
(ii)
Rephrasing this is P("female AND scratch mixing").
The numerator will be the value in the bubble at the end of the branches "scratch mixing" and "female" (15).
This time though we are only choosing from those studying scratch mixing, so the denominator will be at the end of the scratch mixing branch (48).

bold P stretchy left parenthesis " female " space GIVEN thin space " scratch " stretchy right parenthesis bold equals bold 15 over bold 48 stretchy left parenthesis equals 5 over 16 stretchy right parenthesis

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Jamie W

    Author: Jamie W

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.