Trigonometry to Find Angles (Edexcel GCSE Maths) : Revision Note
Did this video help you?
SOHCAHTOA - Finding Angles
How can I use SOHCAHTOA to find missing angles?
STEP 1
Label the sides of the triangle as H, O and AH is the longest side opposite the right angle
O is opposite the given angle
A is next to the given angle
STEP 2
Identify which trigonometric ratio to use: sin, cos or tanWrite down the letters of the lengths you are given
Find the two letters in SOHCAHTOA to identify which ratio to use
If you have O and A then use tan
STEP 3
Substitute the values into the relevant trigonometric formulaThe angle will be unknown
STEP 4
Substitute the fraction into the inverse trigonometric functionYou normally need to press SHIFT on your calculator first
leads to
STEP 5
Type the expression into your calculatorThe question might ask you to round your answer
If not then round to one decimal place
Worked Example
Find the value of the angle ° in the following triangle.
Give your answer to 1 decimal place.
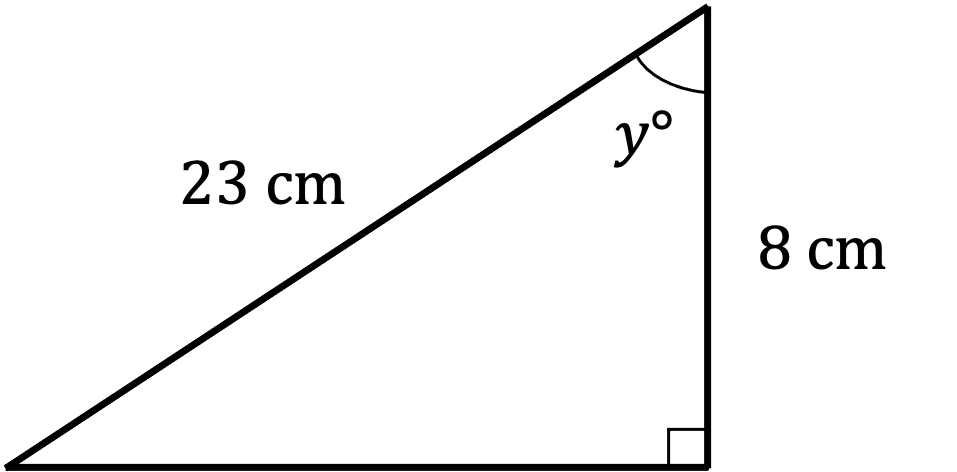
First label the triangle

We know A and H - that's CAH or
Use inverse cos to find
Enter on your calculator
Round to 1 decimal place

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

