GCSEMaths: FoundationEdexcelRevision NotesGeometry & MeasuresCongruence, Similarity & Geometrical ProofSimilarity

Similarity (Edexcel GCSE Maths: Foundation)

Revision Note

Test yourself
Naomi C

Author

Naomi C

Last updated

Similarity

What are similar shapes?

  • Two shapes are similar if they have the same shape and their corresponding sides are in proportion
    • One shape is an enlargement of the other

How do I prove that two triangles are similar?

  • To show that two triangles are similar you need to show that their angles are the same
    • If the angles are the same then corresponding lengths of a triangle will automatically be in proportion
  • You can use angle properties to identify equal angles
    • Look out for for isosceles triangles, vertically opposite angles and angles on parallel lines
  • If a question asks you to prove two triangles are similar
    • For each pair of corresponding angles
      • State that they are of equal size
      • Give a reason for why they are equal 

How do I prove that two shapes are similar?

  • To show that two non-triangular shapes are similar you need to show that their corresponding sides are in proportion
    • Divide the length of one side by the length of the corresponding side on the other shape to find the scale factor 
  • If the scale factor is the same for all corresponding sides, then the shapes are similar

  

Examiner Tip

  • A pair of similar triangles can often be opposite each other in an hourglass formation.
    • Look out for the vertically opposite, equal angles.
    • It may be helpful to sketch the triangles next to each other and facing in the same direction.

Worked example

(a)
Prove that the two rectangles shown in the diagram below are similar.
 

Two similar rectangles 

(a)
Use the corresponding lengths (15 cm and 6 cm) to find the scale factor

15 over 6 space equals space 2.5

Use the corresponding width (5 cm and 2 cm) to find the scale factor for the other pair of sides

5 over 2 equals 2.5

The two rectangles are similar, with a scale factor of 2.5

 

(b)
In the diagram below, AB and CD are parallel lines.
Show that triangles AXB and CDX are similar.

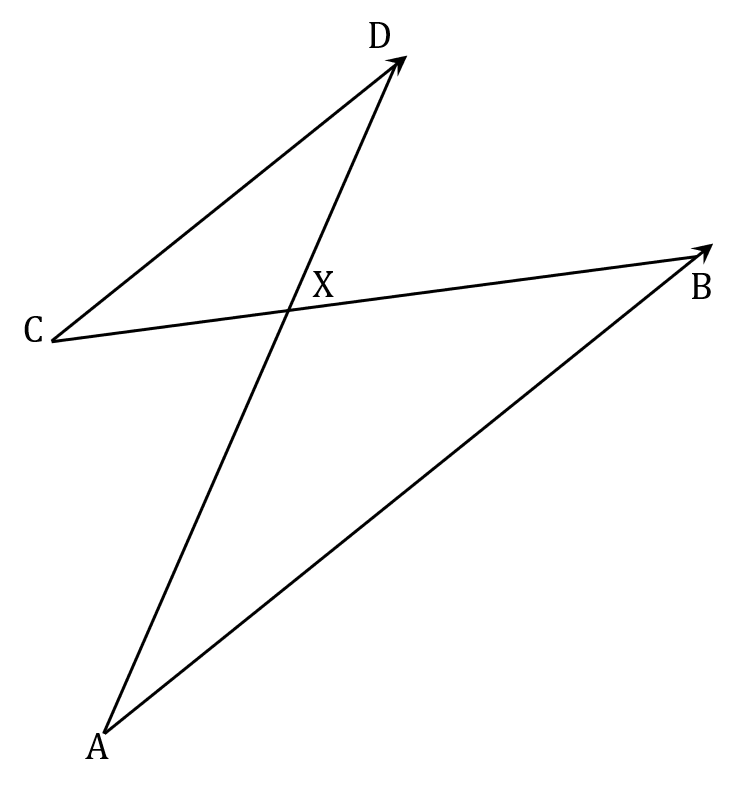
Two similar triangles

State the equal angles by name, along with clear reasons
Don't forget to state that similar triangles need to have equal corresponding angles

Angle AXB  = angle CXD  (vertically opposite angles are equal)
Angle ABC  = angle BCD  (alternate angles on parallel lines are equal)
Angle BAD  = angle ADC  (alternate angles on parallel lines are equal)

All three corresponding angles are equal, so the two triangles are similar

Similar Lengths

How do I find missing lengths on similar shapes?

  • Equivalent lengths in two similar shapes will be in the same ratio and are linked by a scale factor
    • Identify known lengths of corresponding sides
    • Find the scale factor that enlarges the smaller shape onto the bigger shape 
      • Divide a known length on the larger shape by the corresponding known length on the smaller shape
    • Use the scale factor to find the length you need
      • Multiply by the scale factor to find missing lengths on the larger shape
      • Divide by the scale factor to find missing lengths on the smaller shape

Examiner Tip

  • If similar shapes overlap on the diagram (or are not clear) draw them separately.
    • For example, in this diagram the triangles ABC and APQ are similar:
    • Overlapping similar trianglesSo redraw them separately before starting:Similar triangles sketched separately

Worked example

ABCD and PQRS are similar shapes.
Two similar quadrilateralsFind the length of PS.

The two shapes are mathematically similar
Each length on the smaller shape can be multiplied by a scale factor to find the corresponding length on the larger shape

Identify two known corresponding sides of the similar shapes

AB  and PQ  are corresponding sides

Divide the known length on the larger shape by the corresponding length on the smaller shape to find the scale factor

table row cell Scale space Factor space end cell equals cell 6 over 3 equals 2 end cell end table

Divide the length AD  by the scale factor to find its corresponding length PS  on the smaller shape

table row cell P S space end cell equals cell 15 divided by 2 equals 15 over 2 end cell end table

bold italic P bold italic S bold space bold equals bold space bold 7 bold. bold 5 bold space bold cm

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Naomi C

    Author: Naomi C

    Expertise: Maths

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.