Bearings (Edexcel GCSE Maths): Revision Note
Exam code: 1MA1
Did this video help you?
Bearings
What are bearings?
Bearings are a way of describing an angle
They are commonly used in navigation
There are three rules which must be followed when using a bearing:
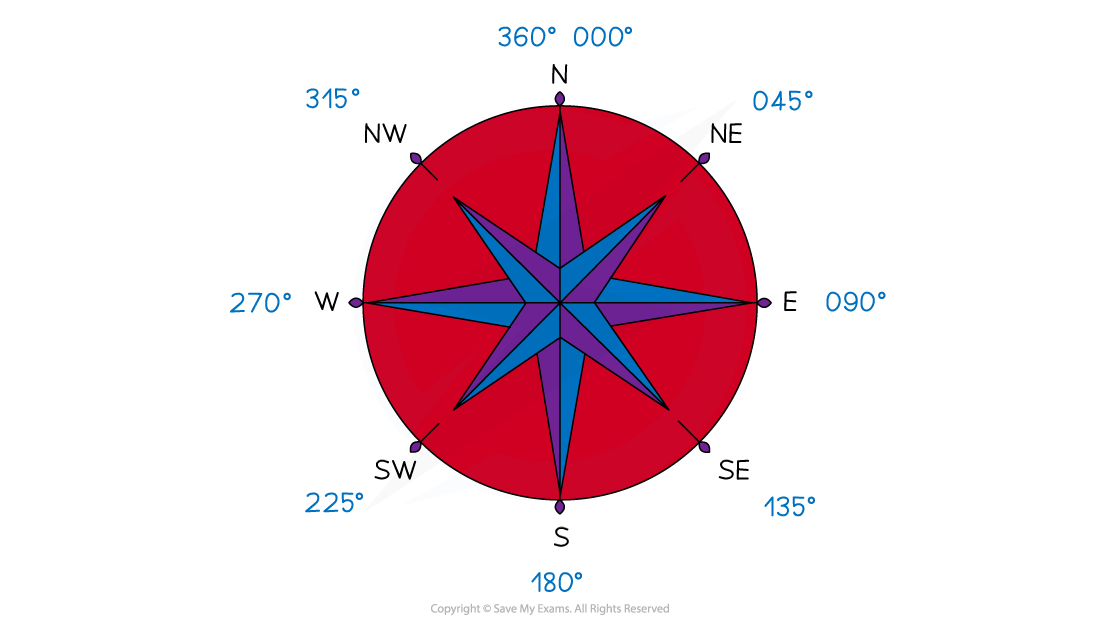
They are measured from North
North is usually straight up on a scale drawing or map, and should be labelled on the diagram
They are measured clockwise
The angle should always be written with 3 digits
059° instead of just 59°
Knowing the compass directions and their respective bearings can be helpful
How do I find a bearing between two points?
Identify where you need to start
"The bearing of A from B" means start at B and find the bearing to A
"The bearing of B from A" means start at A and find the bearing to B
Draw a North line at the starting point
Draw a line between the two points
Measure the angle between the North line and the line joining the points
Measure clockwise from North
Write the angle using 3 figures
How do I draw a point on a bearing?
You might be asked to plot a point that is a given distance from another point and on a given bearing
STEP 1
Draw a North line at the point you wish to measure the bearing fromIf you are given the bearing from A to B draw the North line at A
STEP 2
Measure the angle of the bearing given from the North line in the clockwise directionSTEP 3
Draw a line and add the point B at the given distance
How do I find the bearing of B from A if I know the bearing of A from B?
If the bearing of A from B is less than 180°
Add 180° to it to find the bearing of B from A
If the bearing of A from B is more than 180°
Subtract 180° from it to find the bearing of B from A
How do I answer trickier questions involving bearings?
Bearings questions may involve the use of Pythagoras or trigonometry to find missing distances (lengths) and directions (angles)
You should always draw a diagram if there isn't one given
Examiner Tips and Tricks
Make sure you have all the equipment you need for your maths exams.
A rubber and pencil sharpener can be essential as these questions are all about accuracy. Make sure you can see and read the markings on your ruler and protractor.
Examiner Tips and Tricks
Always draw a big, clear diagram and annotate it, be especially careful to label the angles in the correct places!
Worked Example
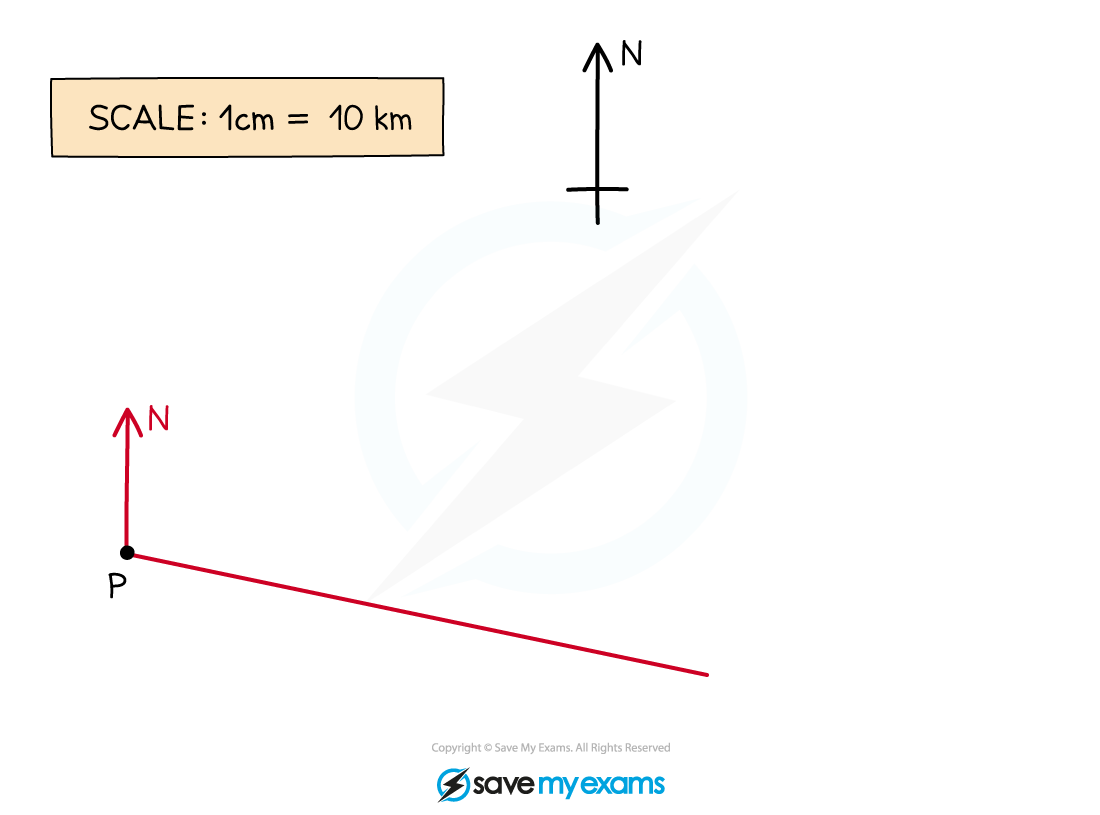
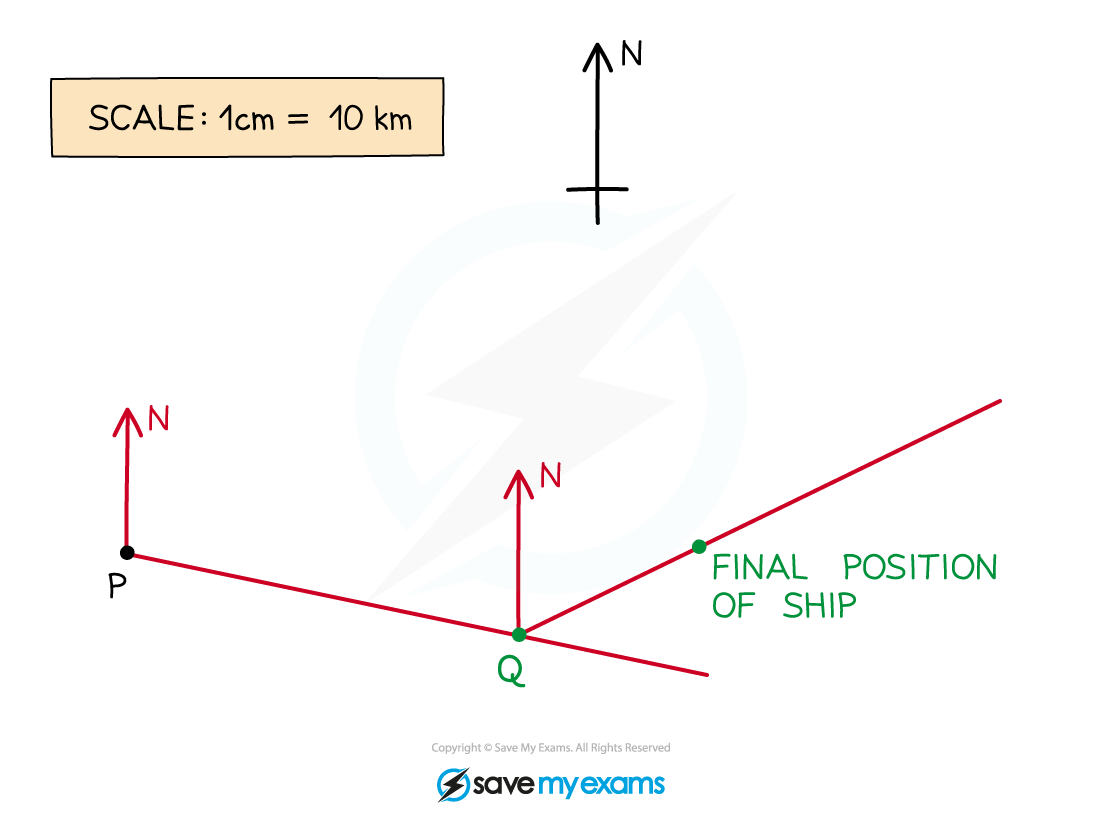
A ship sets sail from the point P, as shown on the map below.
It sails on a bearing of 105° until it reaches the point Q, 70 km away. The ship then changes path and sails on a bearing of 065° for a further 35 km, where its journey finishes.
Show on the map below the point Q and the final position of the ship.

Answer:
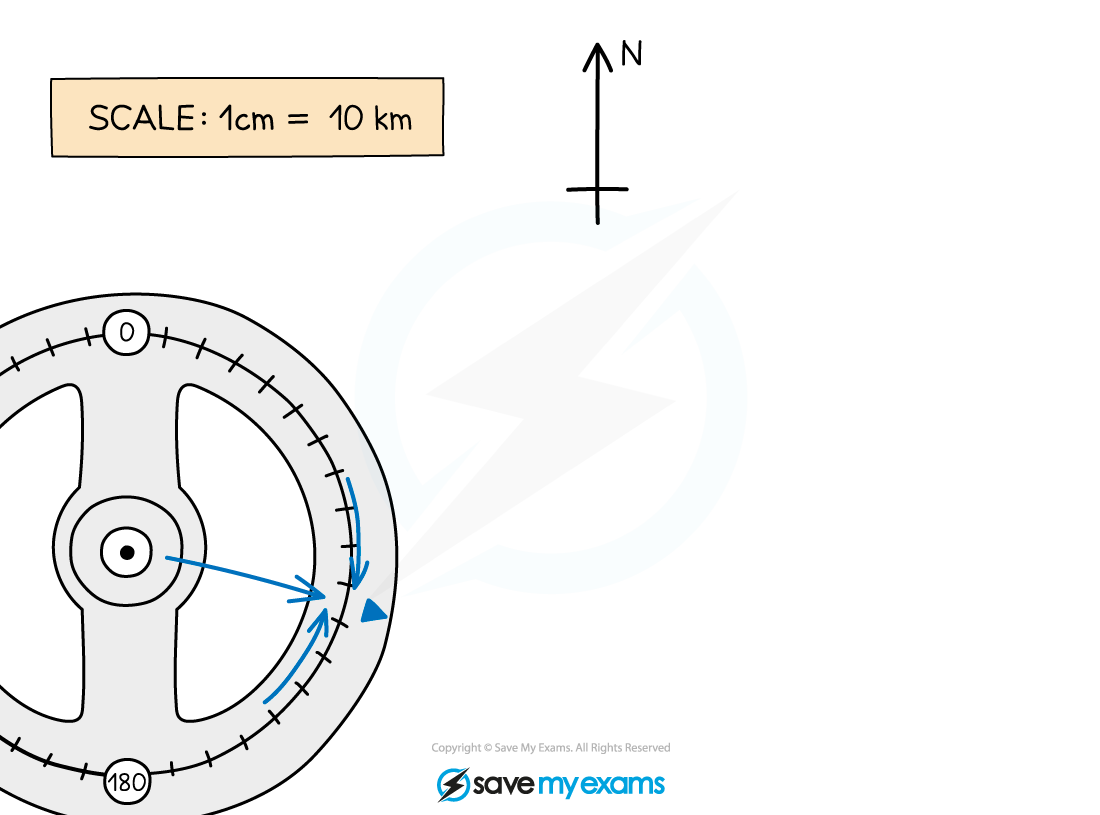
Draw in a north line at the point P
Measure an angle of 105° clockwise from the north line
Making sure you are accurate, carefully make a small but visible mark on the map
Draw a line from P through the mark you have made. Make this line long so that you can easily measure along it accurately
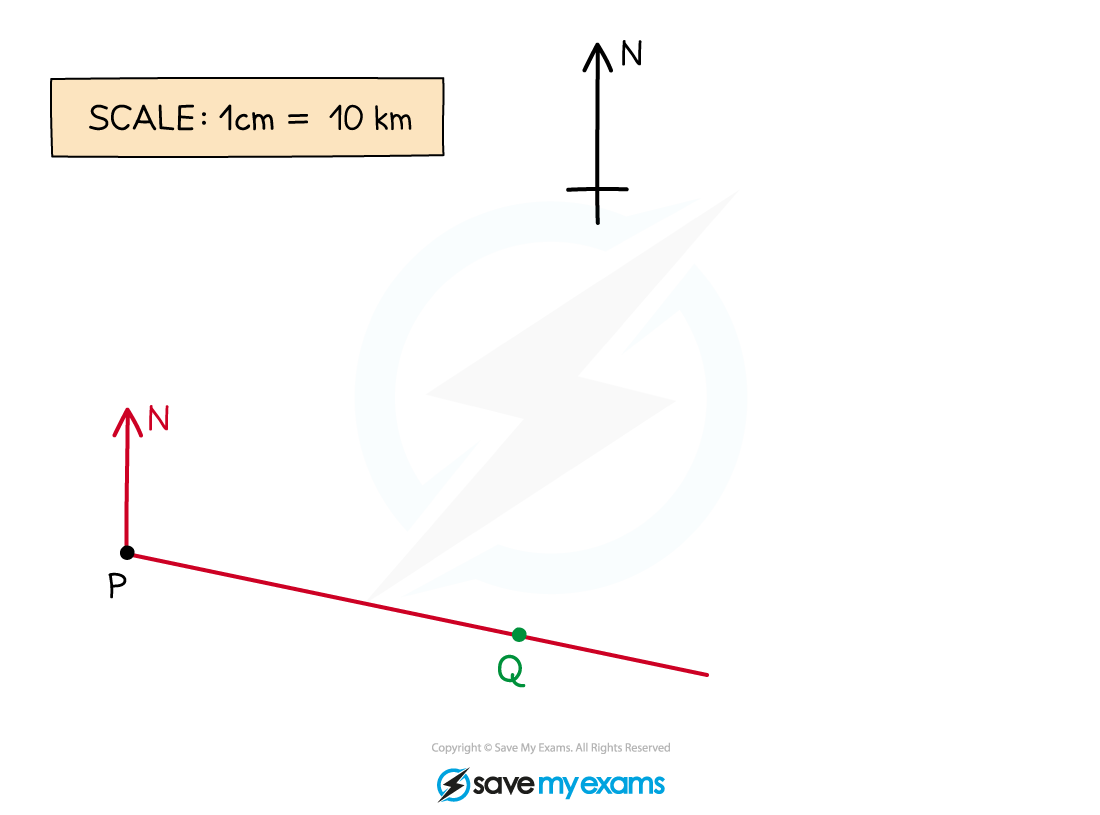
Use the scale given on the map (1 cm = 10 km) to work out the number of cm that would represent 70 km
70 km = 70 ÷ 10 = 7 cm
Accurately measure 7 cm from the point P along the line and make a clear mark on the line
Label this point Q
A bearing of 065 means 65° clockwise from the North
First, draw a North line at the point Q, then carefully measure an angle of 65° clockwise from this line. Make a mark and then draw a line from Q through this mark
Using the scale, find the distance in cm along the line you will need to measure.
35 km = 35 ÷ 10 = 3.5 cm
Accurately measure 3.5 cm from the point Q along this new line and make a clear mark on the line
This is the final position of the ship.

Unlock more, it's free!
Did this page help you?