Basic Percentages (OCR GCSE Maths) : Revision Note
Did this video help you?
Basic Percentages
What is a percentage?
“Per-cent” simply means “out of 100” (or “ ÷ 100”)
Rewriting fractions as percentages means they can be compared more easily
You can do this by finding an equivalent fraction with a denominator of 100
The three percentages are much easier to compare than the three fractions
Percentages are also equivalent to decimals
Notice that a decimal can be converted to a percentage by multiplying by 100
Therefore a percentage can be converted to a decimal by dividing by 100
A fraction can be written as a percentage by finding the decimal equivalent
You could use your calculator to do this
E.g.
How do I find a percentage of an amount without a calculator?
There are some percentages of an amount that are easy to work out
To find 50%, halve the amount
To find 25%, halve the amount twice (finding a quarter)
To find 10%, divide the amount by 10
To find 1%, divide the amount by 100
These percentages can then be used as building blocks to find other percentages, for example:
To find 20%, find 10% and then double it
To find 5%, find 10% and halve it
To find 0.1%, find 1% and divide it by 10
To find 12%, find 10% and 1%, then add together the 10% and two lots of the 1%
To find a percentage larger than 100%, remember that 100% is the original amount
To find 150%, find 50% and add it on to the original amount
How do I find a percentage of an amount with a calculator?
Whilst the methods above can be used with a calculator it is more efficient to use multipliers
A multiplier is the decimal equivalent of a percentage
E.g. To find 12% of 650
Write 12% as a decimal multiplier
12% is equivalent to 0.12
Find the product of the amount and the multiplier, using your calculator
0.12 × 650 = 78
So 12% of 650 is 78
When finding a percentage larger than 100%, the multiplier will be greater than 1
The multiplier for finding 126% of an amount would be 1.26
How do I express one number as a percentage of another?
Start by writing one number as a fraction of the other
Find the decimal equivalent of this fraction using your calculator
or find an equivalent fraction with a denominator of 100
Rewrite this as a percentage
E.g. To find 7 as a percentage of 20
Write as
This is equivalent to
or
So 7 is 35% of 20
Worked Example
Shade 35% of the grid below.
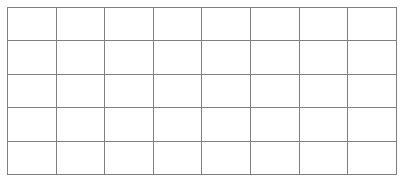
Count the total number of squares in the grid
Total of 40 squares
Find 35% of 40
Start by finding 10%, to help find 5% and 30%
10% of 40 = 4
so 30% of 40 = 4 × 3 = 12
and 5% of 40 = 4 ÷ 2 = 2
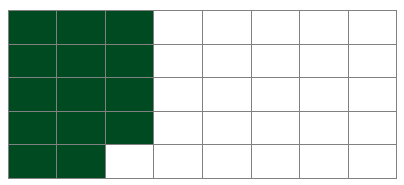
35% of 40 = 12 + 2 = 14
Shade 14 squares
It doesn't matter which 14 you shade
Worked Example
Amber owes $ 1200 for a trip. She has to pay a deposit of $ 150 to secure her place.
Express the deposit as a percentage of the price of the trip.
Write 150 as a fraction of 1200
Find the value of this fraction as a decimal, using your calculator
Write this as the equivalent percentage (by multiplying by 100)
12.5 %

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

