Combination of Transformations

What do I need to know about combined transformations?

Combined transformations are when more than one transformation is performed one after the other
It is often the case that two transformations can be equivalent to one alternative single transformation and you will be expected to describe the single transformation
You will need to have a clear understanding of the following three transformations and their properties to do this

Rotation
- Requires an angle, direction and centre of rotation
- It is usually easy to tell the angle from the orientation of the image
- Use some instinct and a bit of trial and error to find the centre of enlargement.

Rotation-Final-Answer, IGCSE & GCSE Maths revision notes

Reflection
- A reflection will be in a mirror line which can be vertical (x = k), horizontal (y = k) or diagonal (y = mx + c)
- Points on the mirror line do not move
- Double reflections are possible if the mirror line passes through the object

Q1 Reflection Solution, IGCSE & GCSE Maths revision notes

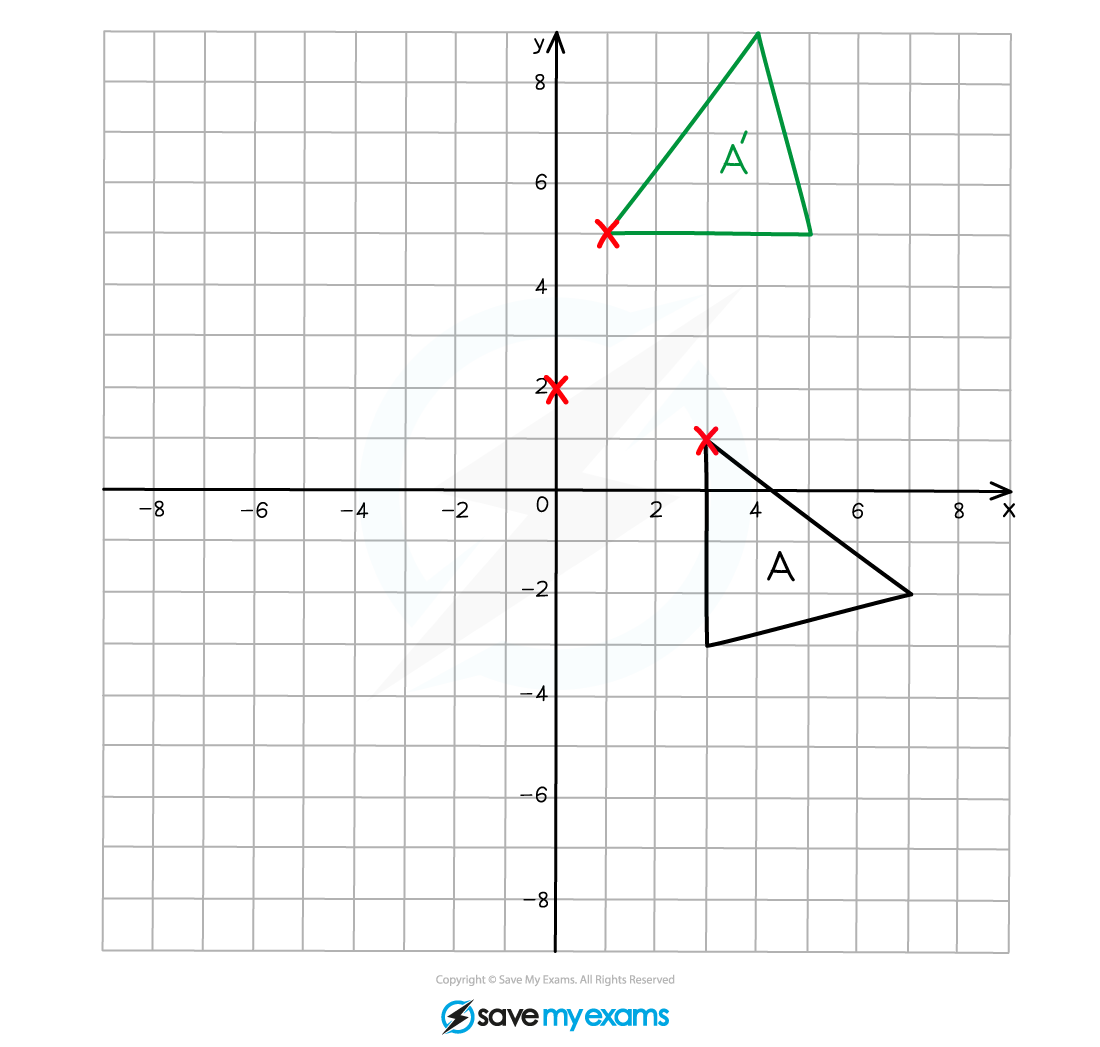
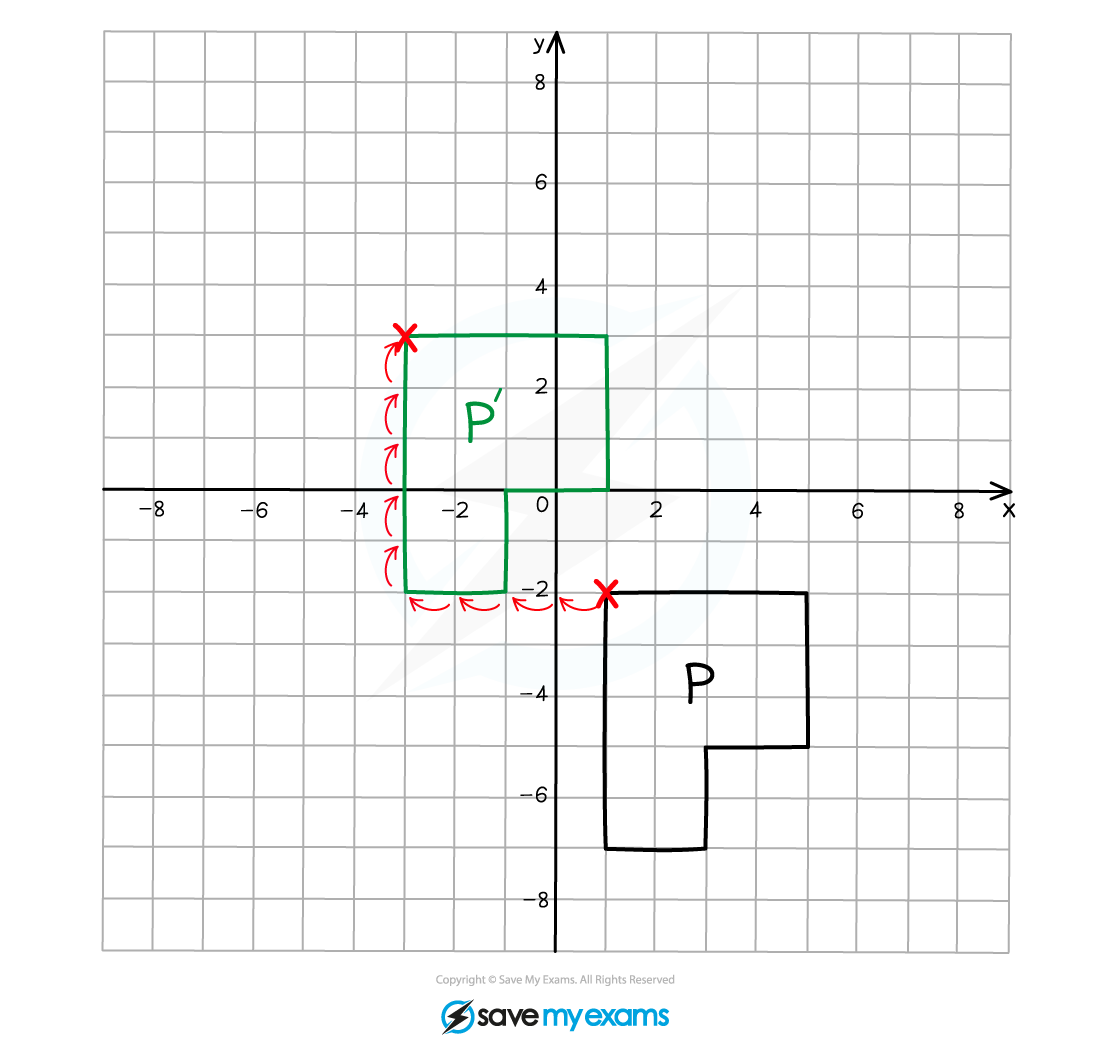
Translation
- A translation is a movement which does not change the direction or size of the shape
- A translation is described by a vector in the form $(x y)$
  - This represents a movement of x units to the right and y units vertically upwards

Q1-Translations-Solution, IGCSE & GCSE Maths revision notes

Note that the transformation enlargement changes the size of the shape and so cannot be a part of a combined transformation

What are common combinations of transformations?

A combination of two reflections can be the same as a single rotation
- One reflection using the line $x = a$ and the other using the line $y = b$
- This is the same as a 180° rotation about the centre $(a, b)$
A combination of a 180° rotation about a centre and an enlargement of scale factor k about the same centre is the same as a single enlargement
- This enlargement would have the same centre but the scale factor would be -k
The order of the combination can be important to the overall effect
- A reflection in the line y = x followed by a reflection in the x-axis is the same as a 90° rotation clockwise about the origin
- A reflection in the x-axis followed by a reflection in the line y = x is the same as a 90° rotation anticlockwise about the origin

What are invariant points?

Invariant points are points that do not change position when a transformation, or combination of transformations, has been performed
- Invariant points return back to their original position

How do I undo a transformation to get back to the original shape?

After transforming shape A to make shape B you might be asked to describe the transformation that maps B to A

Transformation from A to B	Transformation from B to A
Translation by vector $(\begin{matrix} x \\ y \end{matrix})$	Translation by vector $(\begin{matrix} - x \\ - y \end{matrix})$
Reflection in a given line	Reflection in the same line
Rotation by θ° in a direction about the centre $(x, y)$	Rotation by θ° in the opposite direction about the centre $(x, y)$
Enlargement of scale factor $k$ about the centre $(x, y)$	Enlargement of scale factor $\frac{1}{k}$ about the centre $(x, y)$

Examiner Tip

In the exam look out for the word single transformation
- This means you must describe the transformation using only one of the four options

Worked example

(a)

On the grid below rotate shape F 180^o using the origin as the centre of rotation.

Label this shape F'.

(b)

Reflect shape F' in the line

y = 0

Label this shape F''.

(c)

Fully describe the single transformation that would create shape F'' from shape F.

Combined Q1, IGCSE & GCSE Maths revision notes

(a)

Start with a rotation.

Using tracing paper, draw over the original object then place your pencil on the origin and rotate the tracing paper by 180^o.
Mark the position of the rotated image onto the coordinate grid.

Label the rotated image F'.

Combined Q1 Rotation Final, IGCSE & GCSE Maths revision notes

(b)

Now complete the reflection.

The line $y = 0$ is the $x$ - axis.
Measure the perpendicular distance (the vertical distance) between each vertex on the original object and the $x$ -axis, then measure the same distance on the other side of the mirror line and mark on the corresponding vertex on the reflected image.
Repeat this for all of the vertices and join them together to create the reflected image.

Label the reflected image F''.

Combined Q1 Reflection, IGCSE & GCSE Maths revision notes

(c)

You should now be able to see how to get from F to F'' directly.

The object and image are reflections of each other in the $y$ -axis.

Combined Q1 Final Final Answer, IGCSE & GCSE Maths revision notes

The single transformation from F to F'' is a reflection in the $y$ -axis

Stating the $y$ -axis or the equation $x = 0$ are both acceptable

Combination of Transformations (OCR GCSE Maths)

Revision Note