Revision NotesExam QuestionsPast Papers
GCSEMathsOCRRevision Notes9. Congruence & SimilarityCongruence, Similarity & Geometrical ProofGeometrical Proof

Geometrical Proof (OCR GCSE Maths)

Revision Note

Dan

Author

Dan

Last updated

Geometrical Proof

What is a geometrical proof?

  • Geometric proof involves using known rules about geometry to prove a new statement about geometry
  • A proof question might start with “Prove…” or “Show that …”
  • The rules that you might need to use to complete a proof include;
    • Properties of 2D shapes - in particular of isosceles triangles and quadrilaterals
    • Basic angle properties
    • Angles in polygons
    • Angles in parallel lines
    • Congruence and similarity
    • Circle theorems
    • Pythagoras theorem
  • You will need to be familiar with the vocabulary of the topics above, in order to fully answer many geometrical proof questions

How do I write a geometrical proof?

  • Usually you will need to write down two or three steps to prove the statement
  • At each step, you should write down a fact and a reason, especially if asked in the question to show reasons. Write it in the form "[fact] , [mathematical reason]"
    • For example, “AB = CD, opposite sides of a rectangle are equal length”
  • The proof is complete when you have written down all the steps clearly
  • It’s a good idea to start by underlining key words in the question - and if they’re not already, mark any of the information from the question on the diagram
  • Use the diagram! Add key information such as angles or line lengths to the diagram as you work through the steps - but you must write them down in your written answer too!

What notation should I use?

  • Labelling vertices (corners) and lengths are done in capital letters
    • e.g. "from A to B ..."
    • e.g. "side lengths AB and BC are equal..."
    • e.g. "triangle ABC is ..."
  • Labelling angles can be done by writing "angle ABC"
    • other shorthand ways include A B with hat on top C or ∠ABC
    • if referring to angle x for ease, then you should label x on the diagram and define what x is
      • e.g. "x is acute, where x = angle BAC"

What phrases can I say?

  • There are common phrases that are sufficient as explanations and should be learnt
  • For triangles and quadrilaterals,
    • "angles in a triangle sum to 180"
    • the triangle is "isosceles" / "equilateral" / "right-angled"
    • "base angles in an isosceles triangle are equal"
    • the length is ... "by Pythagoras"
    • "angles in a quadrilateral sum to 360"
  • For straight lines,
    • "parallel" / "perpendicular"
    • the points are "collinear" (lie on the same straight line)
    • "midpoint"
  • For angles at points,
    • "vertically opposite angles are equal"
    • "angles on a straight line sum to 180"
    • "angles at a point sum to 360"
  • For angles in polygons,
    • "exterior angles sum to 360"
    • "interior angles sum to 180(n - 2)"
  • For angles in parallel lines,
    • "alternate angles are equal"
    • "corresponding angles are equal"
    • "co-interior angles sum to 180"
  • For congruent or similar shapes,
    • triangle ABC is "congruent to" triangle PQR
    • shape X and shape Y are "similar" 
  • For circle theorems,
    • "two radii make an isosceles triangle"
    • "angle at centre is twice angle at circumference"
    • "angle in a semicircle is 90"
    • "radius bisects chord at right-angles"
    • "radius meets tangent at right-angles"
    • "opposite angles in cyclic quadrilateral sum to 180"
    • "angles in same segment are equal"
    • "alternate segment theorem"

Examiner Tip

  • DO show all the key steps - if in doubt, include it
  • DON'T write in full sentences! For each step, just write down the fact, followed by the key mathematical reason that justifies it

Worked example

In the diagram below, AC and DG are parallel lines. B lies on AC, E and F lie on DG and triangle BEF is isosceles.

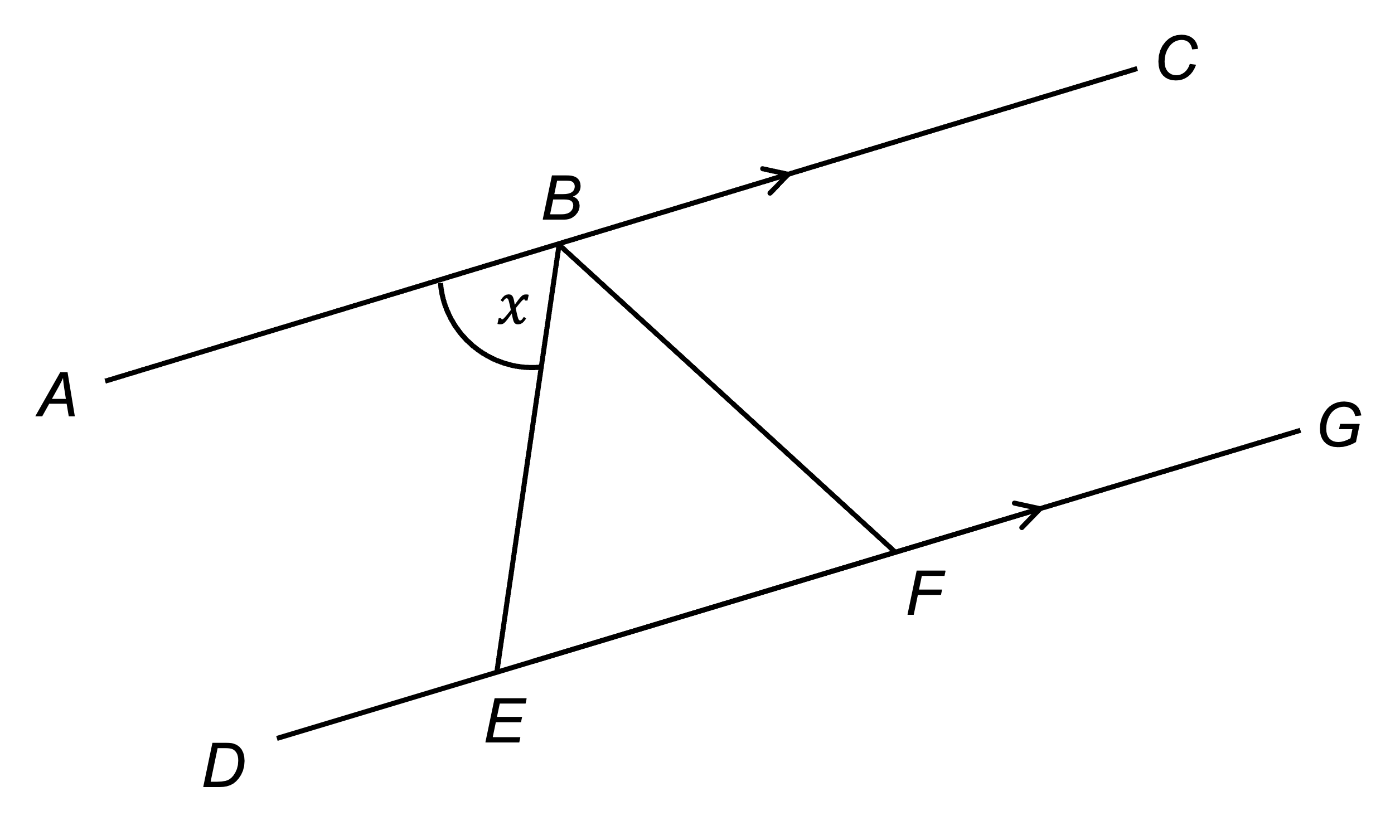
4-5-3-geometrical-proof-we

Prove that angle EBF is 180 minus 2 x. Give reasons for each stage of your working.

Mark on the diagram that triangle BEF is isosceles.

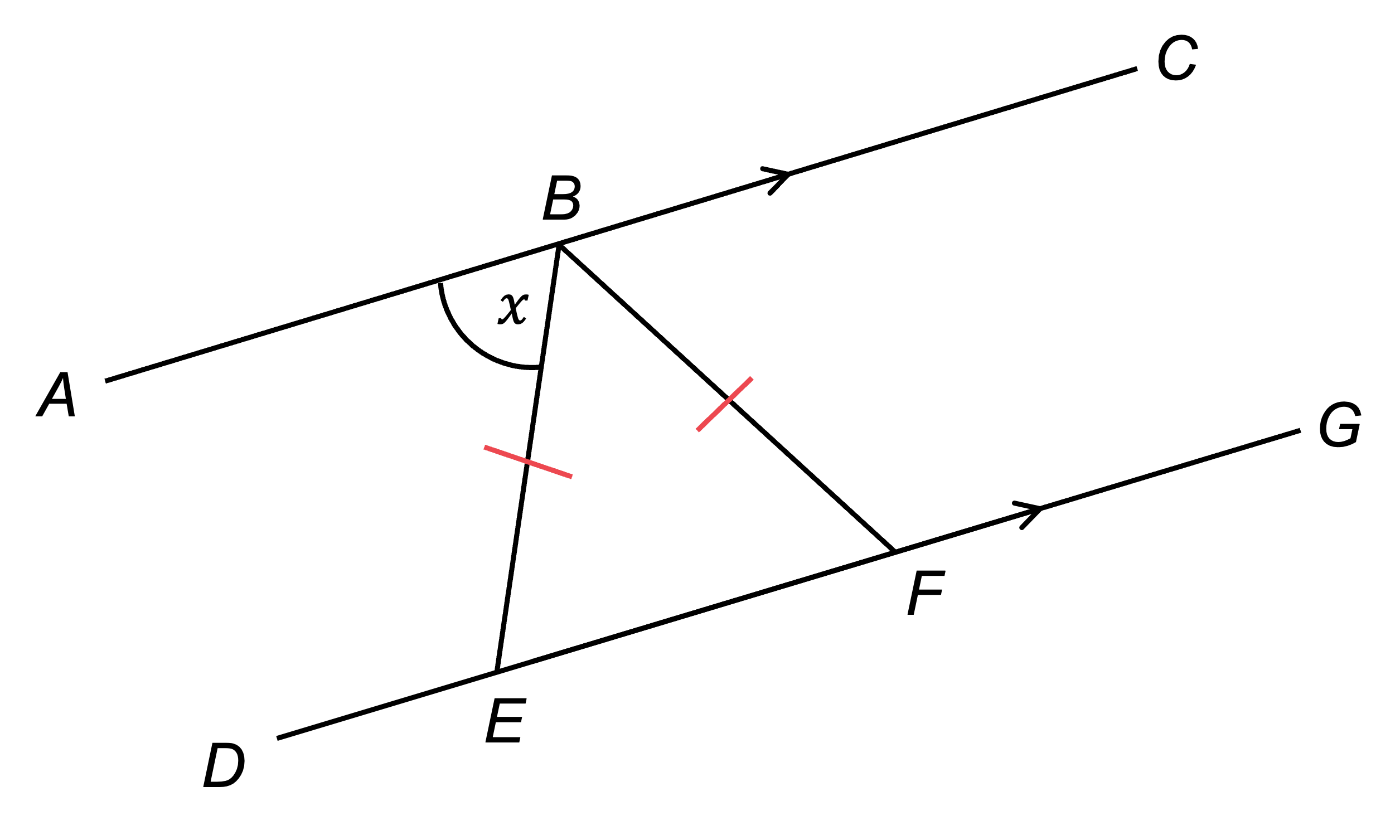
4-5-3-geometrical-proof-we-answer1

AC and DG are parallel lines, so using alternate angles we know that angle BEF = x. Mark this on the diagram.

4-5-3-geometrical-proof-we-answer2

Write the fact, and the reason using the key mathematical vocabulary

angle BEF = bold italic x, alternate angles

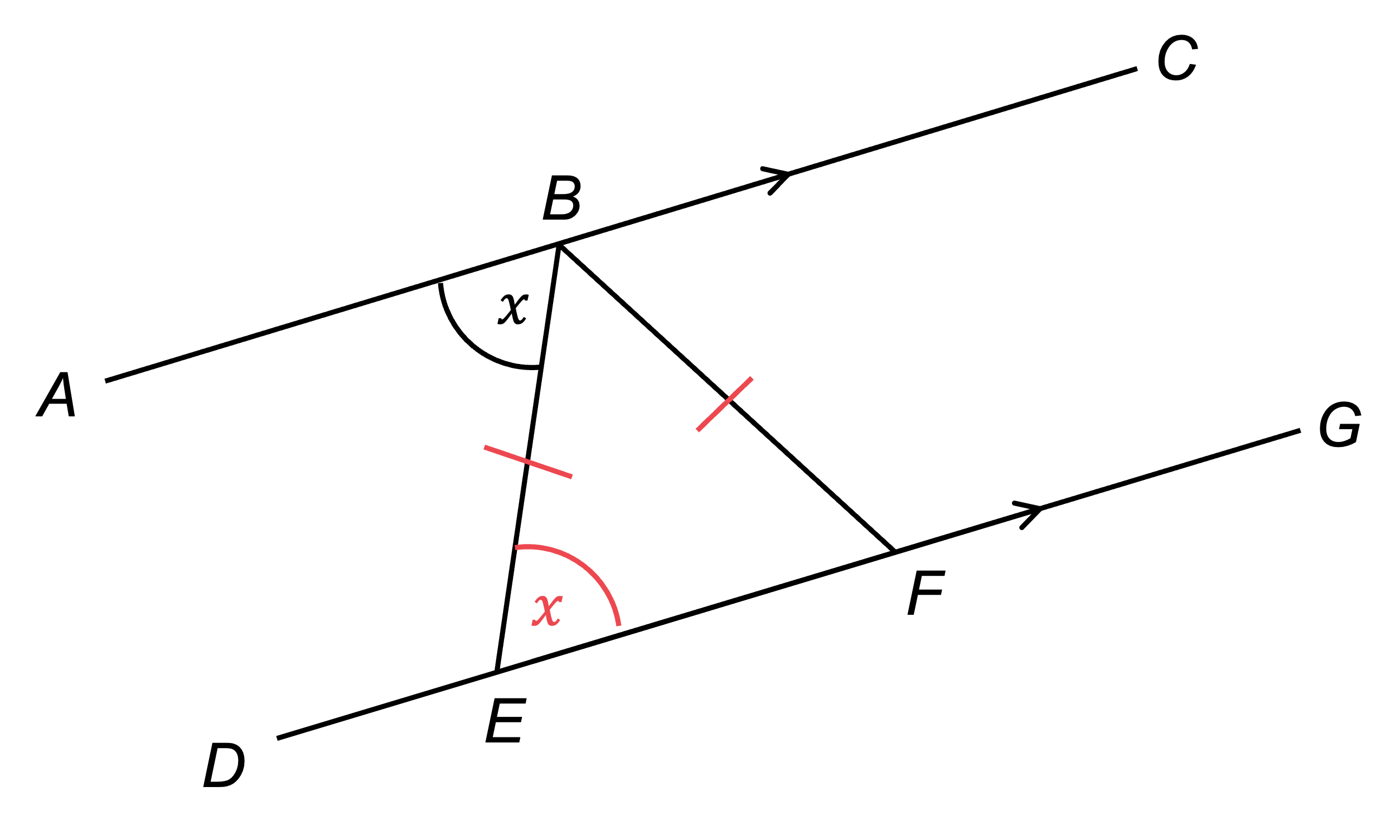
Now using the fact that triangle BEF is isosceles, we can see that angle BFE = x. Mark this on the diagram.

4-5-3-geometrical-proof-we-answer3

Write the fact, and the reason using the key mathematical vocabulary

angle BFE = bold italic x, isosceles triangle

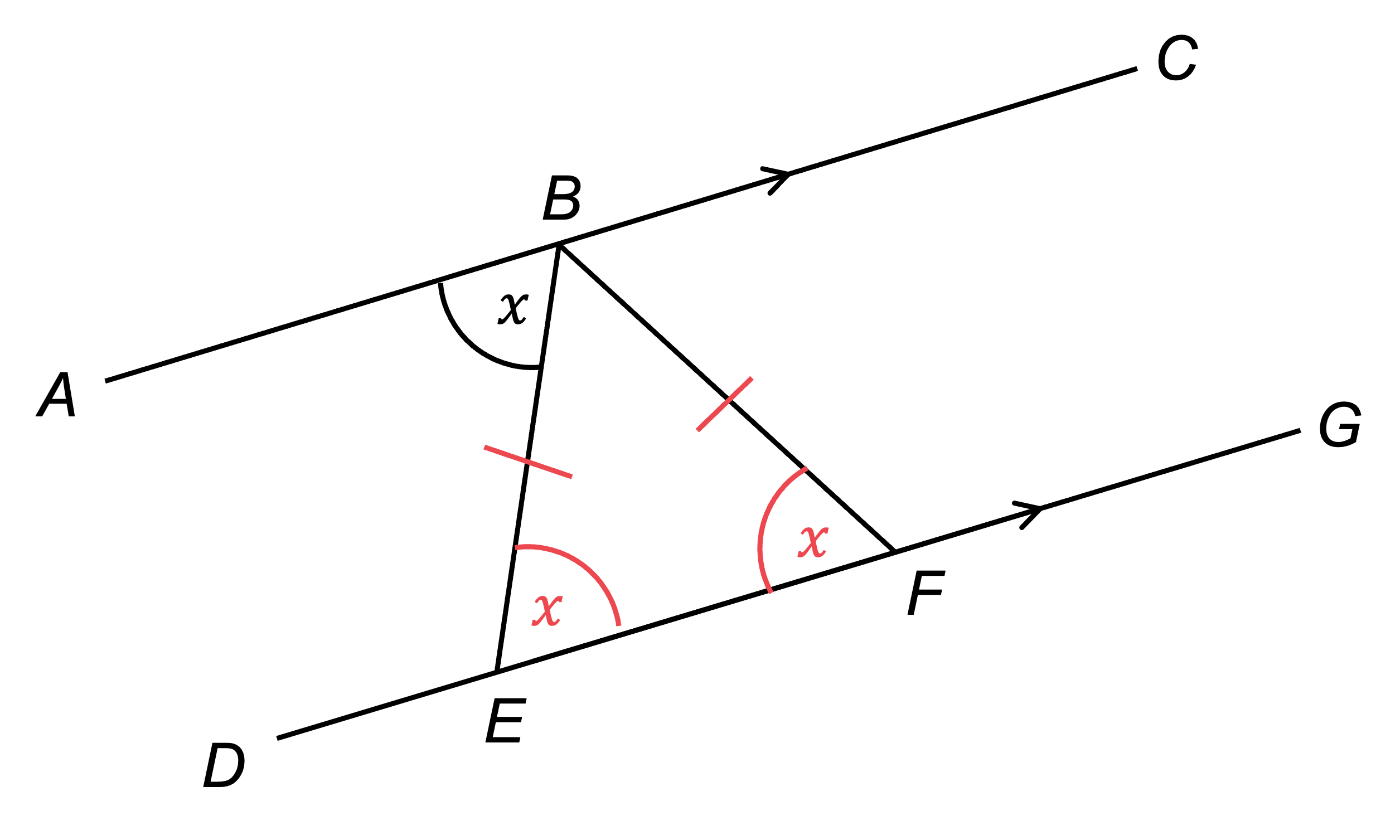
Now we can see that angle EBF is the last remaining angle in a triangle, and as the angles in a triangle sum to 180, angle EBF = 180 minus 2 x

Write the fact, and the reason using the key mathematical vocabulary

angle EBF = bold 180 bold minus bold 2 bold italic x, angles in a triangle sum to 180

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:SimilarityNext:Similar Areas & Volumes
    Dan

    Author: Dan

    Expertise: Maths

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.