Graphing Inequalities (OCR GCSE Maths)

On the axes given below, show the region that satisfies the three inequalities;

           

Label the region R.

First draw the three straight lines, ,  and , using your knowledge of Straight Line Graphs (y = mx + c). You may wish to rearrange  to the form  first:

The line takes a solid line because of the "≥" while the lines  and  take dotted lines because of the "<"

Now we need to shade the unwanted regions

For (or ), the unwanted region is below the line. We can check this with the point (0, 0);

is false therefore (0, 0) does lie in the unwanted region for 

For , the unwanted region is above the line. If unsure, check with another point, for example (1, 0)

is true, so (1, 0) lies in the wanted (i.e. unshaded) region for 

For , shade the unwanted region to the right of . If unsure, check with a point

Finally, don't forget to label the region R

Write down the three inequalities which define the shaded region on the axes below.

First, using your knowledge of Straight Line Graphs (y = mx + c), define the three lines as equations, ignoring inequality signs;

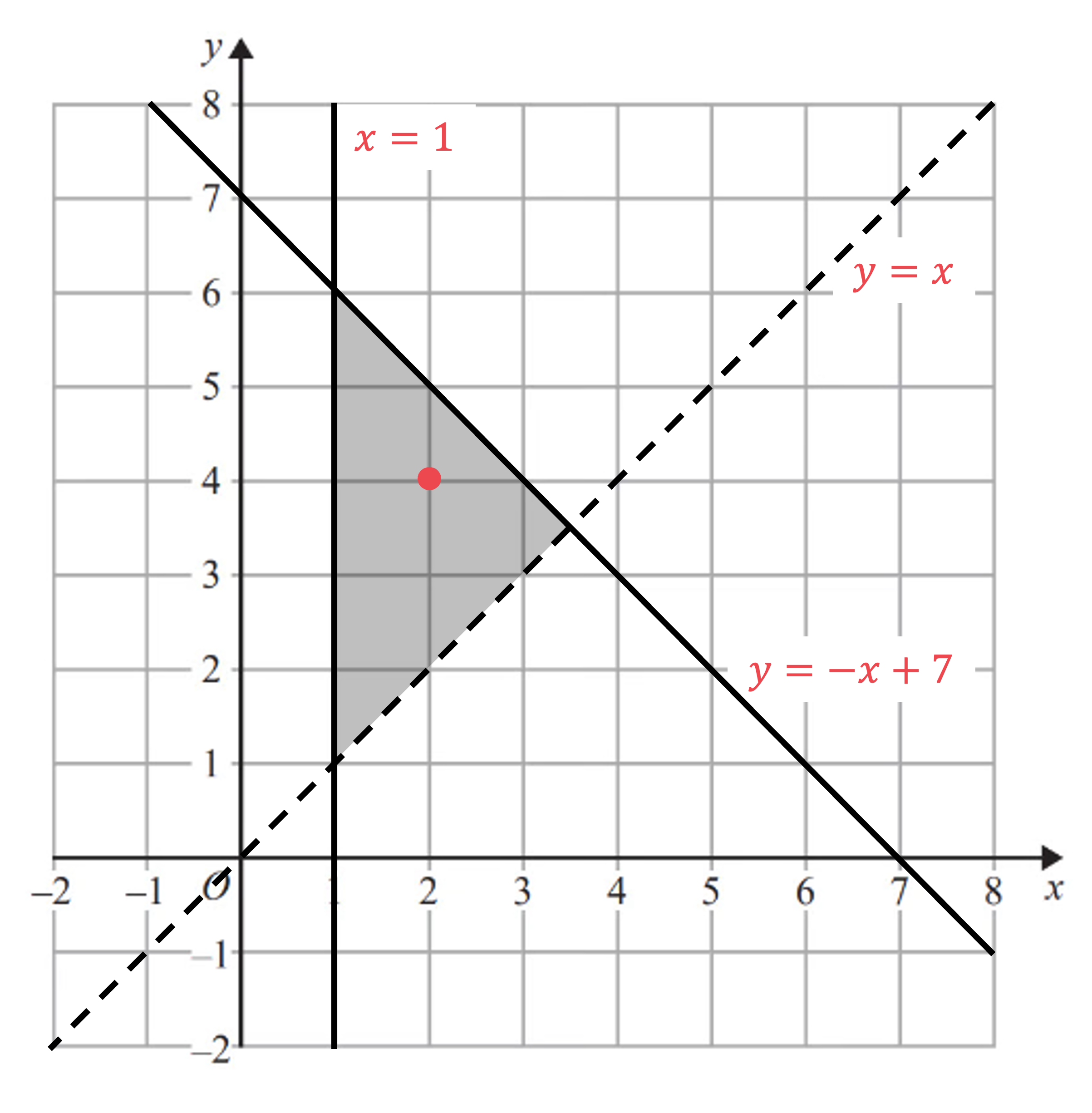
Now decide which inequality signs to use

For $y=x$, the shaded region is above the line, and the line is dotted, so the inequality is

$\mathit{y}\mathbf{>}\mathit{x}$

Check by substituting a point within the shaded region into this inequality. For example, using (2, 4) as marked on the graph above;

"$4>2$" is true, so the inequality $y>x$ is correct

For $y=-x+7$, the shaded region is below the line, and the line is solid, so the inequality is 

$\mathit{y}\mathbf{\le }\mathbf{-}\mathit{x}\mathbf{+}\mathbf{7}$
or $\mathit{y}\mathbf{+}\mathit{x}\mathbf{\le }\mathbf{7}$

Again, check by substituting (2, 4) into the inequality;

"$4\le -2+7$" is true, so the inequality $y\le -x+7$ is correct

For $x=1$, the shaded region is to the right of the solid line so the inequality is

$\mathit{x}\mathbf{\ge }\mathbf{1}$

(Vertical and horizontal inequality lines probably do not need checking with a point, though do so if you are unsure)