Conditional Probability (OCR GCSE Maths): Revision Note
Did this video help you?
Conditional Probability
What is a conditional probability?
A conditional probability is the probability of something happening (A) given that something else has already happened (B)
It is written
Pronounced "the probability of A given B"
How do I calculate conditional probabilities?
Conditional probabilities must be out of a smaller restricted set of outcomes (not out of all possible events)
For example, if a computer randomly selects a digit from 1, 2, 3, 4, 5, 6, 7, 8, 9
P(it select a multiple of three) =
This is not a conditional probability
There are 3 possibilities (3, 6, 9) out of all 9 possibilities
However, if you program the computer to only select from even numbers, then
P(it selects a multiple of three given that it selects an even number) =
1 possibility (6) out of only 4 possibilities (2, 4, 6, 8)
This is a conditional probability, written P(multiple of 3 | even) =
Examiner Tips and Tricks
Look out for conditional probability questions within larger questions on two-way tables, Venn diagrams or tree diagrams
They often use the phrase given that
Worked Example
A Venn diagram is shown below.
Find , simplifying your answer.
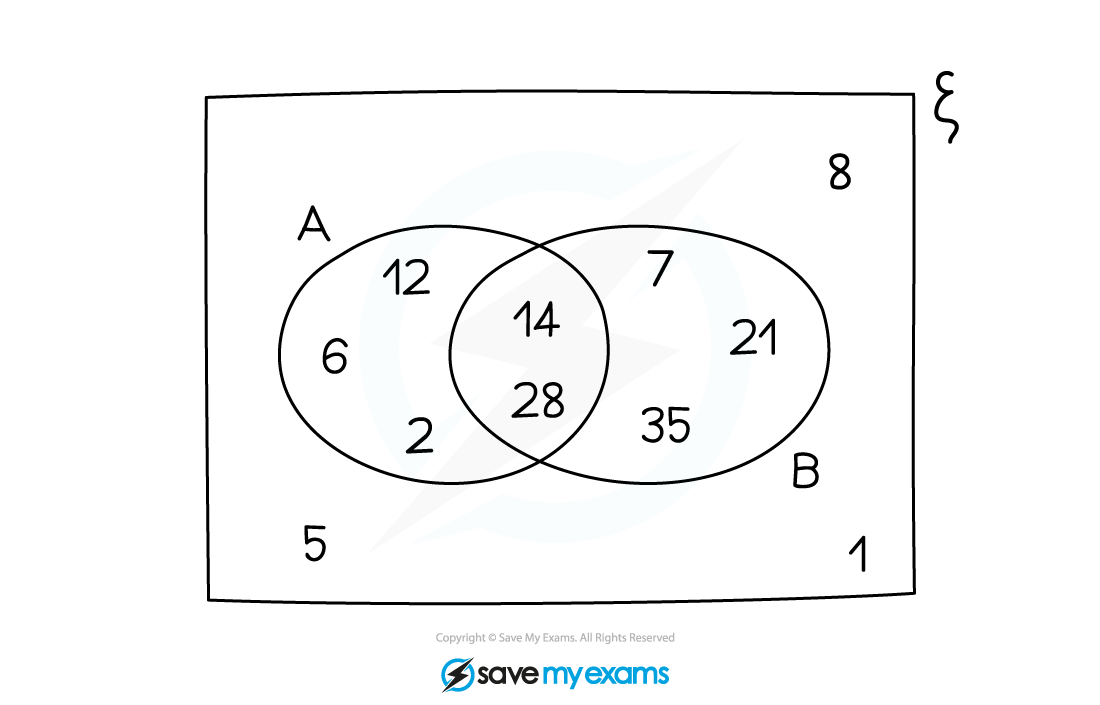
means the probability that A happens, given that B has already happened
Given that B has already happened, your probability will be out of the total number in B
Find the total number in B
14 + 28 + 7 + 35 + 21 = 105
Out of this total number in B, find how many are in A
14 + 28 = 42
Form a probability by dividing 42 by 105
Simplify your answer

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

