Problem Solving with Areas (OCR GCSE Maths) : Revision Note
Problem Solving with Areas
What is problem solving?
Problem solving, usually has two key features:
A question is given as a real-life scenario
eg. Mary is painting a bedroom in her house...
There is usually more than one topic of maths you will need in order to answer the question
eg. Area and percentages
What are common problems that involve area?
Area is a commonly used topic of 'real-world' maths
For example, laying a carpet, painting a house or designing a sports field all involve area
Typically, the 'real-world' scenarios also have a cost
A lot of area problems also involve calculations with money
How do I solve problems that involve area?
There is often a lot of text in a problem solving question, which can make it seem harder than it is
Avoid focusing only on what the question asks you, think about what you can do with the information given
This may lead you to think of something else you can do
Eventually you may be able to see your way to answering the original question
Think about the context of the question, what makes sense?
Look out for key information in the text:
Real-life context
A question involving the size of a field, will mean be talking about its area
Key words
Types of measure: area, length, cost, ...
Conditions: minimum, maximum, greatest, ...
Units
You may see compound units, e.g. $/m2 , these may help you to identify calculations that you need to do
Annotate diagrams with information that you can work out
Remember to do this in pencil in case you need to erase it!
Problem solving questions could appear on either a non-calculator paper or a calculator paper
Examiner Tips and Tricks
Even if you never get to a final answer always try to do some maths with the information from the question
You are likely to score some extra marks from your working!
Worked Example
John wants a new carpet for the lounge in his house.
A sketch of his lounge is given below.
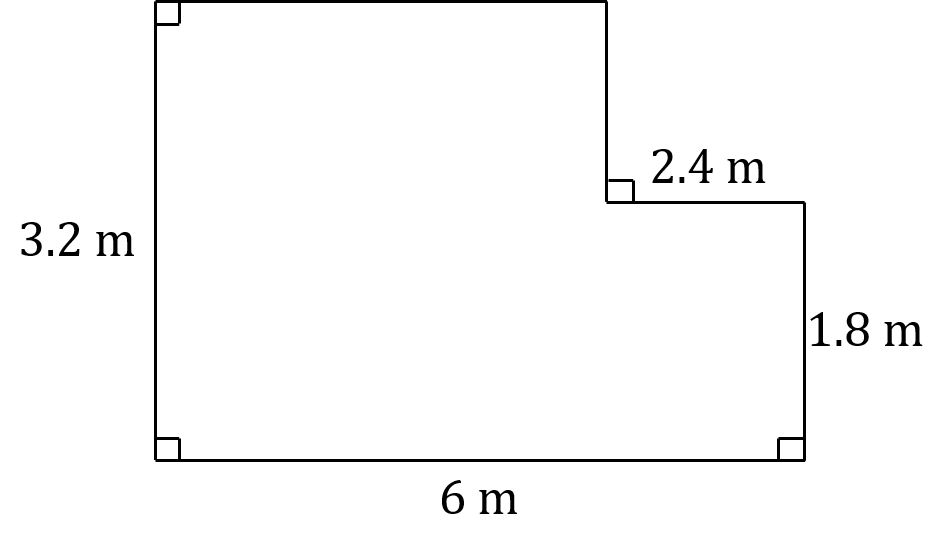
He gets quote from two local companies, Company A and Company B.
The amount they charge for laying a carpet is given below.
Company A: Fixed price of $5.50 per square metre
Company B: $6 per square metre for the first ten square metres, then $4 per square metre for anything over that.
Which company should John choose in order to keep the cost of laying the carpet to a minimum?
Although this question doesn't specifically tell you you need to find the area, it is implied as the costs both use 'square metre'
The shape of the lounge is a compound shape consisting of two rectangles
Split the area into these two rectangles and find the missing distances by subtracting the smaller length (2.4 m) from the longer one (6 m)
6 - 2.4 = 3.6
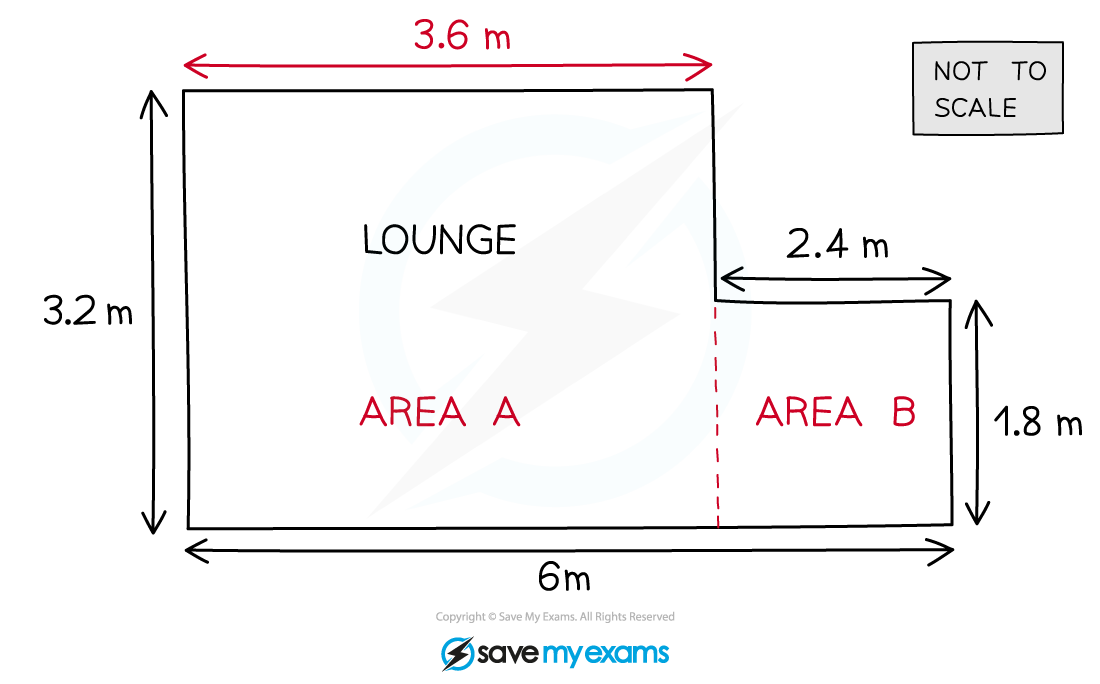
Find the area of the lounge by adding the two areas together
Find the cost for each of the two companies separately
Company A:
Company B:
John should choose Company B as it will cost $3.76 less than Company A

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

