Equation of a Tangent (OCR GCSE Maths) : Revision Note
Did this video help you?
Equation of a Tangent
How do we find the equation of a tangent to a circle?
First, make sure you are familiar with equations of straight lines and perpendicular lines
A tangent just touches a circle (but does not cross it)
The tangent at point P is perpendicular to the radius OP
remember, the gradients of perpendicular lines multiply to -1
they are negative reciprocals
So if P is a point
on the circumference, then the gradient of the radius OP is
.
Therefore the gradient of the tangent to the circle at P is
From here, use
to find the equation of the tangent
Examiner Tips and Tricks
Solving simultaneous equations of circle and tangent only gives one solution
so if you are asked to show a line is a tangent, solve the simultaneous equations and show there is only one solution
Always draw a diagram to help!
Worked Example
The graph shows the circle with the equation .
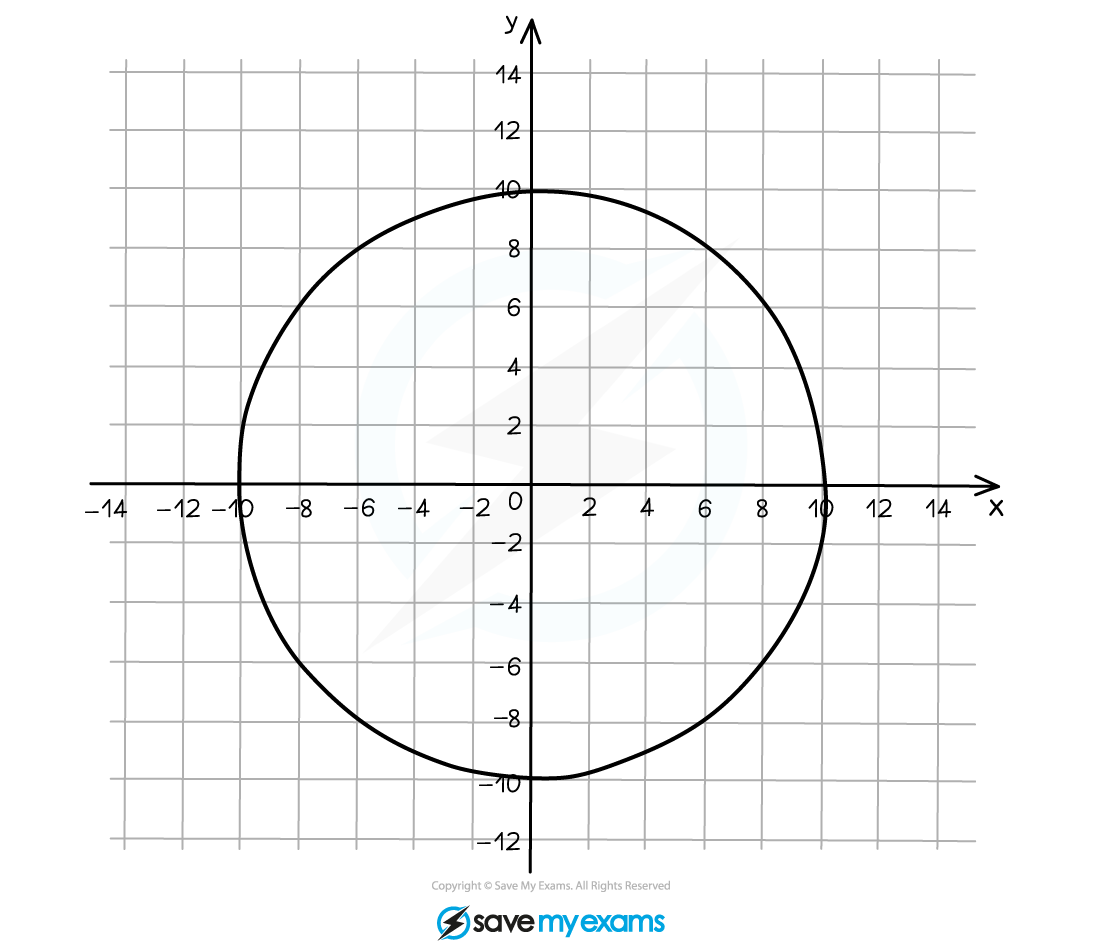
Find an equation of the tangent to the circle at the point .
Find the gradient of the radius by finding te gradient of the line segment form the origin to the point
Find the gradient of the tangent by taking the negative reciprocal of the gradient of the radius
Substitute ,
and
into
to find the value of
The equation of the tangent is

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
