Revision NotesExam QuestionsFlashcardsPast Papers
GCSEMathsEdexcelHigherRevision Notes4. Geometry & MeasuresSine, Cosine Rule & Area of TrianglesThe Cosine Rule

The Cosine Rule (Edexcel GCSE Maths)

Revision Note

Naomi C

Written by: Naomi C

Reviewed by: Dan Finlay

Did this video help you?

Cosine Rule

What is the cosine rule?

  • The cosine rule is used in non right-angled triangles

    • It allows us to find missing side lengths or angles

  • It states that for any triangle

a squared equals b squared plus c squared minus 2 b c space cos space A

  • Where

    • a is the side opposite angle A

    • b and c are the other two sides

      • b and c are either side of angle A

      • A is the angle between them

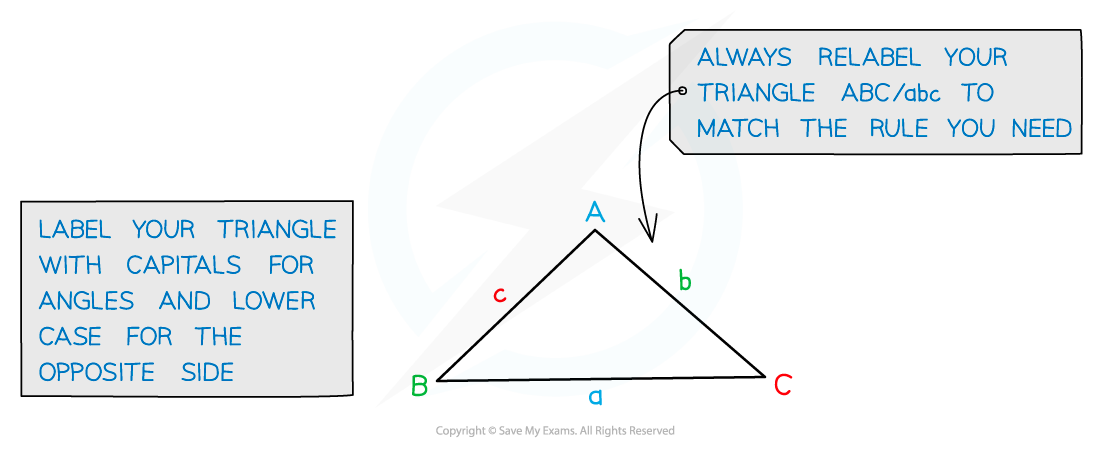
Non Right-Angled Triangle labelled with angles A, B and C and opposite corresponding sides a, b and c.

How do I use the cosine rule to find a missing length?

  • Use the cosine rule for lengths

    • when you have two sides and the angle between them

    • and you want to find the opposite side, a

  • Start by labelling your triangle with the angles and sides

    • Angles have upper case letters

    • Sides opposite the angles have the equivalent lower case letter

  • Substitute values into a squared equals b squared plus c squared minus 2 b c space cos space A

    • Make a the subject (don't forget to square root)

How do I use the cosine rule to find a missing angle?

  • Use the cosine rule for angles

    • when you have all three sides

    • and you want to find an angle

  • It helps to rearrange the formula as follows, by adding 2 b c space cos space A to both sides then making cos space A the subject

table row cell a squared end cell equals cell b squared plus c squared minus 2 b c space cos space A end cell row cell a squared plus 2 b c space cos space A end cell equals cell b squared plus c squared end cell row cell 2 b c space cos space A end cell equals cell b squared plus c squared minus a squared end cell row cell cos space A end cell equals cell fraction numerator b squared plus c squared minus a squared over denominator 2 b c end fraction end cell end table

  • Use the formula table row cell cos space A end cell equals cell fraction numerator b squared plus c squared minus a squared over denominator 2 b c end fraction end cell end table to find the unknown angle A

    • Remember, A is the angle between sides b and c

      • (you may need to relabel the triangle)

    • You will need to use inverse cosine at the end, cos to the power of negative 1 end exponent open parentheses... close parentheses

  • Unlike the sine rule, there is no ambiguous case of the cosine rule

Examiner Tips and Tricks

  • You are given the cosine rule in the form a squared equals b squared plus c squared minus 2 b c space cos space A on the formula sheet

  • Getting an error on your calculator when finding an angle may mean you have rearranged the formula incorrectly

Worked Example

The following diagram shows triangle ABC, where AB space equals space 4.2 space km, BC space equals space 3.8 space km and AC space equals space 7.1 space km.

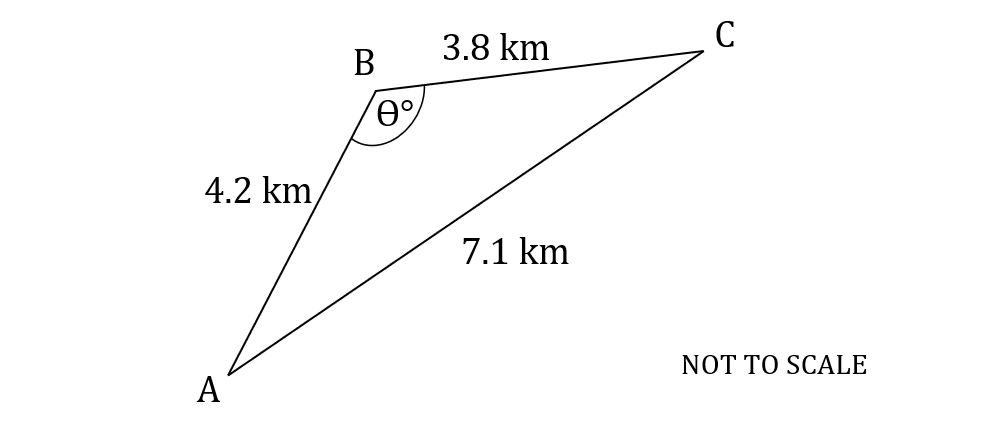
Triangle ABC with AB = 4.2 km, BC = 3.8 km, AC = 7.1 km and angle ABC = θº.

Calculate the value of angle ABC.

The side opposite the angle is 7.1, so a equals 7.1

The sides 4.2 and 3.8 are b and c (in either order)

Use the cosine rule in the rearranged form cos space A equals fraction numerator b squared plus c squared minus a squared over denominator 2 b c end fraction

table row cell cos space theta end cell equals cell fraction numerator 4.2 squared plus 3.8 squared minus 7.1 squared over denominator 2 open parentheses 4.2 close parentheses open parentheses 3.8 close parentheses end fraction end cell row theta equals cell cos to the power of negative 1 end exponent open parentheses fraction numerator 4.2 squared plus 3.8 squared minus 7.1 squared over denominator 2 open parentheses 4.2 close parentheses open parentheses 3.8 close parentheses end fraction close parentheses end cell row theta equals cell 125.04699... end cell end table

bold italic theta bold equals bold 125 bold. bold 0 bold degree (to 1 d.p.)

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:The Sine RuleNext:Area of a Triangle
    Author
    Reviewer
    Naomi C

    Author: Naomi C

    Expertise: Maths

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.