Circle Theorem Proofs (Edexcel GCSE Maths) : Revision Note
Circle Theorem Proofs
How do I prove circle theorems using radii to form isosceles triangles?
This type of proof can be used to prove the following circle theorems
The angle in a semicircle is always 90°
The angle at the centre is twice the angle at the circumference
Angles in the same segment are equal
Opposite angles in a cyclic quadrilateral add up to 180°
How do I prove that the angle in a semicircle is 90°?
This circle theorem states that an angle subtended at the circumference of a semicircle is always a right angle
Although it is a special case of the angle at the centre and circumference circle theorem, it can be proved without using any other circle theorems
STEP 1
Draw a radius from the centre of the circle to the angle subtended at the circumferenceThis will form two isosceles triangles
STEP 2
Label the two angles formed at the angle subtended at the circumferenceand
.
The angle you are trying to prove is 90° is now
STEP 3
Label the remaining angles in each of the isosceles triangles with algebraic expressions in terms ofand
Angles at the base of an isosceles triangle are equal
Therefore the two remaining angles at the circumference are also
and
Angles in a triangle add up to 180°
Therefore each angle at the centre will be labelled with the expression
and

STEP 4
The angles at the centre lie on a diameter, which is a straight line, thereforeRearrange this equation to show that
In STEP 2 you already labeled the angle at the circumference as
, so this proves that the angle at the circumference equals 90°
Give clear reasons throughout your proof, using the key words given in bold
How do I prove that the angle at the centre is twice the angle at the circumference?
This circle theorem states that an angle subtended at the centre of a circle is twice the angle subtended at the circumference of a circle from the same arc
It does not need any other circle theorems to prove it
STEPS 1, 2 and 3 are the same as above

STEP 4
The three angles formed at the centre lie at a point, therefore they will add to 360°Label the third angle at the centre θ, then you can form the equation
Rearrange this equation to show that
In STEP 2 you already labelled the angle at the circumference as
, so this proves that the angle at the centre is twice the angle at the circumference
Give clear reasons throughout your proof, using the keywords given in bold
This circle theorem is also a more generic version of the circle theorem the angle in a semicircle is always 90°
You could be asked to prove either without the use of any circle theorems
How do I prove that angles at the circumference from the same arc are equal?
This circle theorem states that any angles subtended at the circumference of a circle from the same arc are equal
This theorem is proved using the circle theorem an angle subtended at the centre of a circle is twice the angle subtended at the circumference of a circle
Draw the radii from the centre of the circle to the points on the circumference forming the arc which the angles are subtended from
This will form an angle at the centre, label this angle
By the circle theorem "The angle and the centre is twice the angle at the circumference", any angle at the circumference can be labelled

You do not need to prove the circle theorem you have used in this proof, but you must give clear reasons
How do I prove that opposite angles in a cyclic quadrilateral add up to 180°?
This theorem is proved using the circle theorem "An angle subtended at the centre of a circle is twice the angle subtended at the circumference of a circle"
STEP 1
Draw the radii from the centre of the circle to any two of the vertices of the cyclic quadrilateral that are opposite each otherThis will form two angles at the centre, label these angles
and
The angles
and
are at a point, so they add up to 360°
Therefore
which can be simplified to
STEP 2
By the circle theorem "The angle and the centre is twice the angle at the circumference", the two angles at the circumference can be labelledand
We have already shown that

You do not need to prove the circle theorem you have used in this proof, but you must give clear reasons
How do I prove circle theorems involving chords and tangents?
This type of proof can be used to prove the following circle theorems
The perpendicular from the centre of a circle bisects a chord
The tangent to a circle meets the radius at 90°
The alternate segment theorem
These proofs can be more tricky and will use other circle theorems within them
The questions will often guide you through the proof
The circle theorem "The perpendicular from the centre of a circle bisects a chord' can be proved using congruent triangles
If the radius is perpendicular to the chord, two right-angled triangles will be formed
Prove that these two triangle are congruent using the RHS (right angle, hypotenuse, side) rule
The chord and the radius are perpendicular, therefore both triangles have a right angle
The hypotenuse is the line from the centre to the circumference, therefore both triangles have an equal hypotenuse
The line joining the chord to the centre is shared between both triangles, therefore this is a same side in both triangles
Therefore, by RHS, the two triangles are congruent

If the two triangles are congruent, then all three sides will be the same and so the perpendicular must bisect the chord
The proof for the circle theorem "The tangent to a circle meets the radius at a right angle" uses proof by contradiction and involves assuming that they do not meet at 90° and proving that this is not possible
The proof for the alternate segment theorem uses the circle theorems 'the angle in a semicircle is always 90°' and 'the tangent to a circle meets the radius at 90°'
Examiner Tips and Tricks
If you are unsure of how to start a proof question, begin by drawing in the radii from the centre to any significant point on the circumference and look for isosceles triangles
The question may tell you not to use any circle theorems in your proof, in this case you will most likely be looking for isosceles triangles
Worked Example
In the diagram below, ,
and
are points on the circumference of a circle, centre
.
is a tangent to the circle.
Prove that angle and angle
are equal.
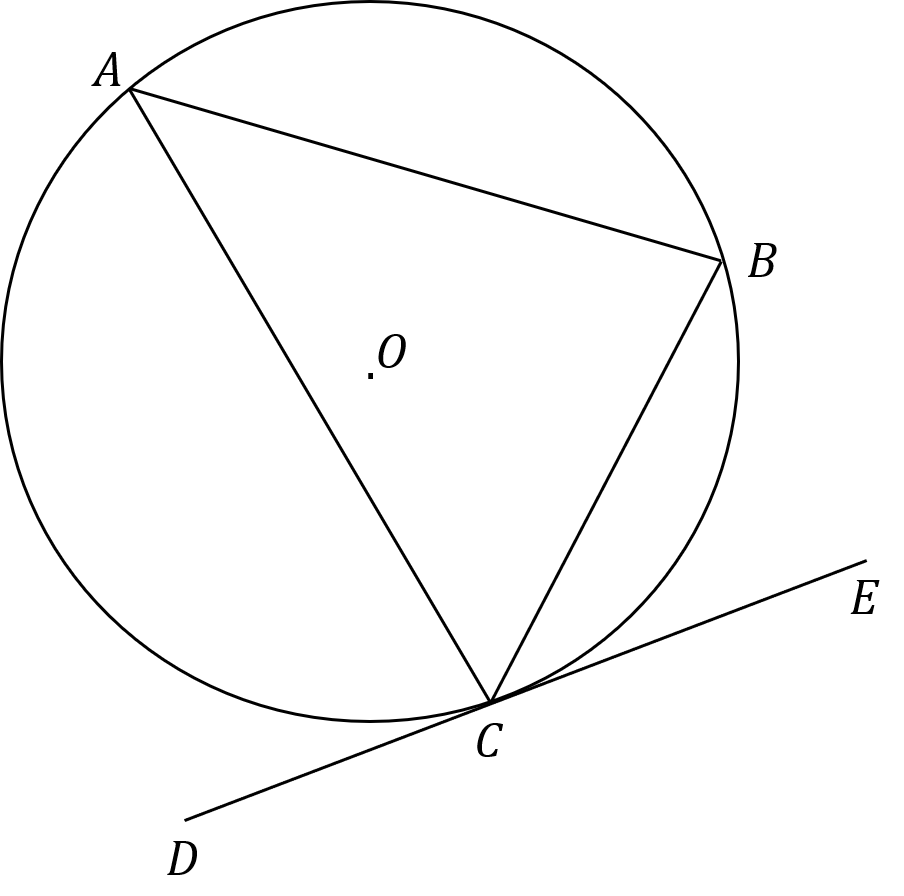
Begin by joining the point O to the point C and continue the line through to the circumference so that a diameter is drawn on the diagram.
Label this new point on the circumference F.
Join the point F to the point B on the circumference.
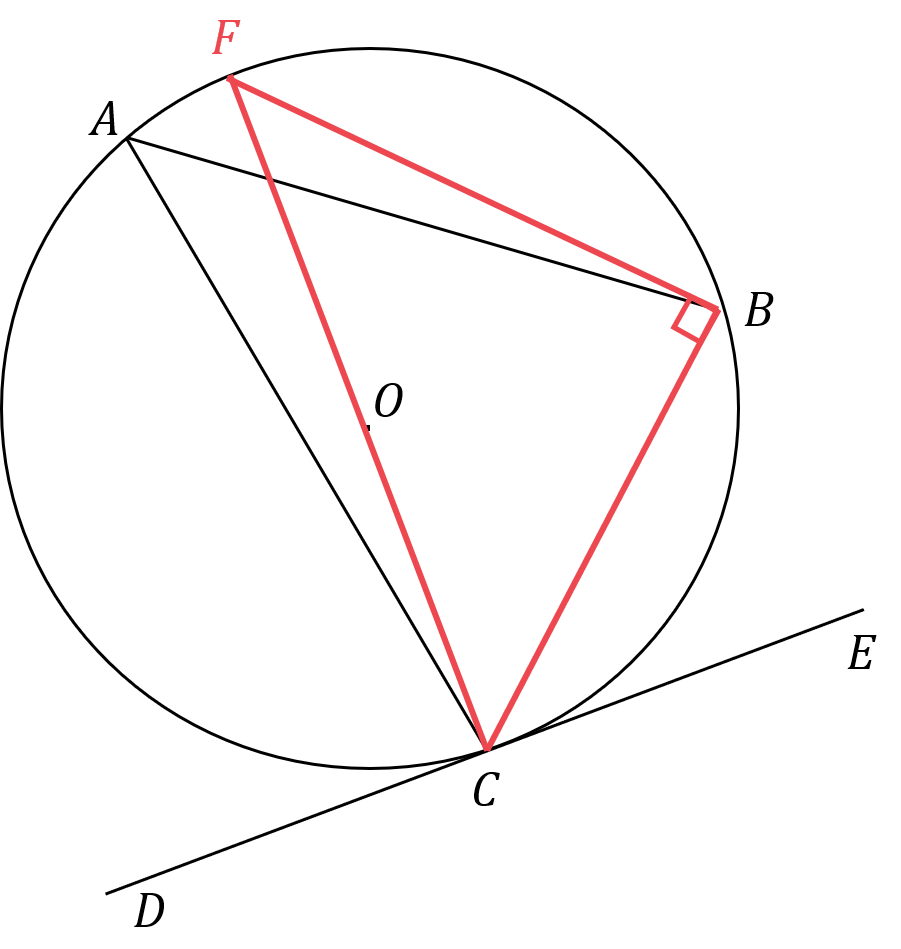
Angle CBF = 90°
The angle in a semicircle is always 90°
The line OC is a radius, so it will meet the tangent DE at 90°.
Let angle .
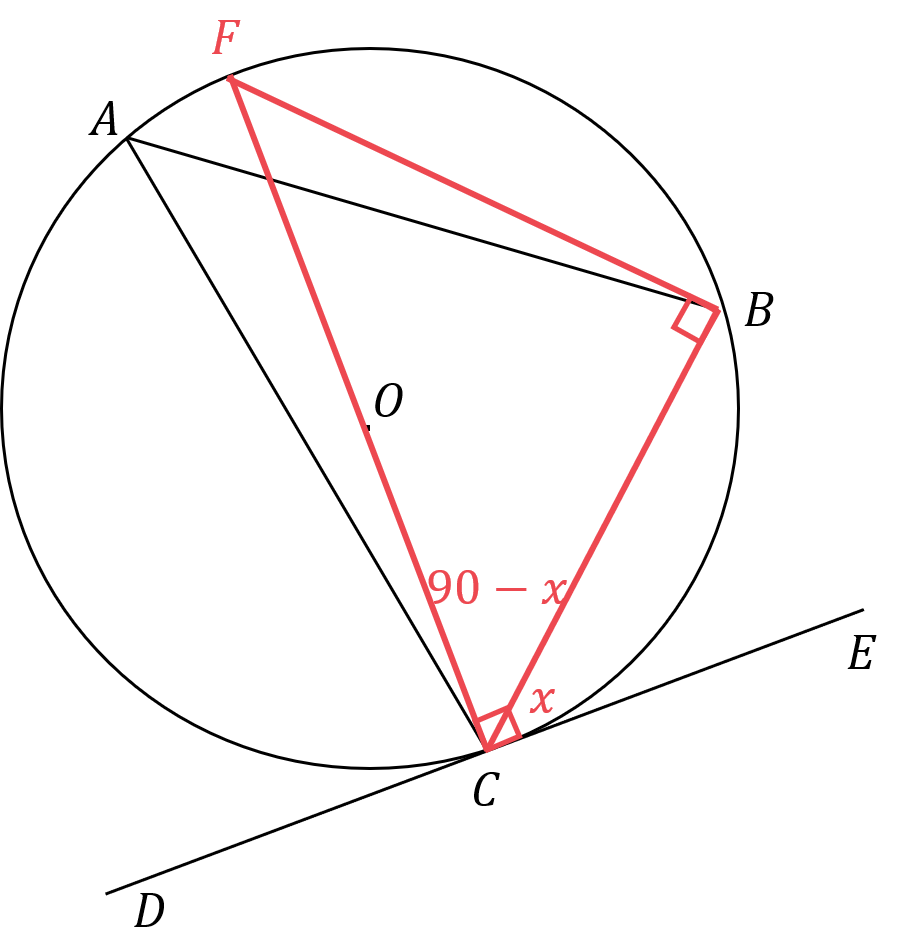
Angle
The radius meets a tangent at 90°
Angles in a triangle add up to 180°, use this to find the angle CFB in terms of .
The angles in a triangle add up to 180°
Angles subtended at the circumference from the same arc are equal.
Use this to find an expression for angle BAC in terms of .
We have already stated that .
Therefore Angle BCE = Angle BAC

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
