Constructions (Edexcel GCSE Maths) : Revision Note
Constructions
What are constructions?
A construction is a process where you create an accurate geometric object using a pair of compasses and a straight edge (and a pencil)
There are several types of construction you must be able to carry out:
A perpendicular bisector of a line
This is a line that cuts another one exactly in half (bisects) but also crosses it at a right angle (perpendicular)
It shows a path that is equidistant (equal distance) between the two endpoints of the line
A perpendicular from a point to a line
This is the shortest path between the point and the line
It will meet the line at a right angle
An angle bisector
This is a line that cuts an angle exactly in half (bisects)
It shows a path that is equidistant (equal distance) between the two lines that form the angle
How do I construct a perpendicular bisector of a line?
STEP 1
Set the distance between the point of the compasses and the pencil to be more than half the length of the lineSTEP 2
Place the point of the compasses on one end of the line and sketch an arc above and below the lineSTEP 3
Keeping your compasses set to the same distance, place the point of the compasses on the other end of the line and sketch an arc above and below the lineThe arcs should intersect each other both above and below the line
STEP 4
Connect the points where the arcs intersect with a straight line

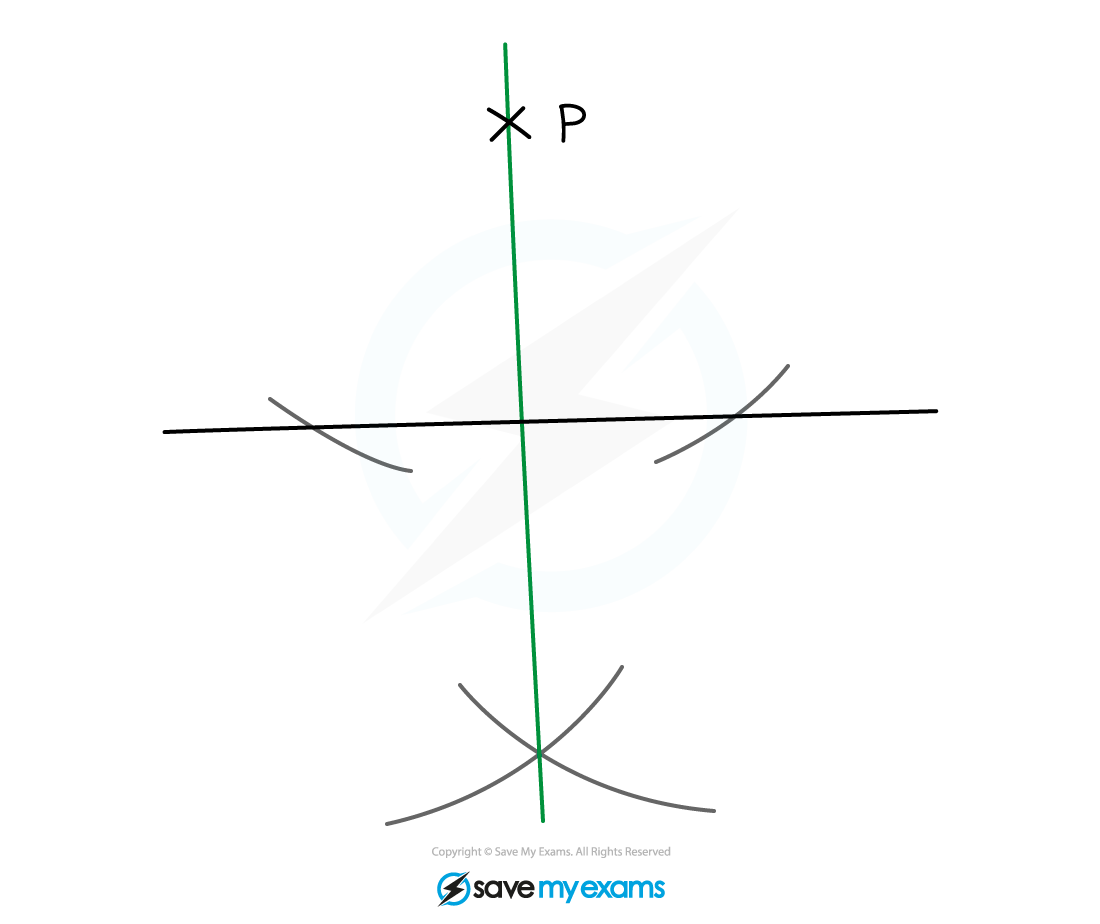
How do I construct a perpendicular from a point to a line?
STEP 1
Set the distance between the point of your compasses and the pencil to be greater than the distance between the point P and the lineSTEP 2
Placing the point of the compasses on the point P, draw an arc that intersects the line in two placesSTEP 3
Set the distance between the point of the compasses and the pencil to be more than half the distance between the two points of intersection on the lineSTEP 4
Place the point of the compasses on one point of intersection and sketch an arc on the opposite side of the line to PSTEP 5
Keeping your compasses set to the same distance, place the point of the compasses on the other point of intersection and sketch an another arcThe arcs should intersect
STEP 6
Connect the point where the arcs intersect to point P with a straight line
How do I construct an angle bisector?
STEP 1
Set the distance between the point of your compasses and the pencil to be about half the distance of the smallest line that makes the angleThe precise distance is not important
STEP 2
Place the point of the compasses where the lines meet and sketch an arc that intersects both of the lines that form the angleSTEP 3
Keeping your compasses set to the same distance, place the point of the compasses on one of the points of intersection and sketch an arcSTEP 4
Keeping your compasses set to the same distance, place the point of the compasses on the other point of intersection and sketch an arcThis should intersect the last arc you drew
STEP 5
Join the point of the angle to the point of intersection with a straight line

Examiner Tips and Tricks
Make sure you have all the equipment you need for the exam; pen, pencil, ruler, compasses, protractor, calculator
An eraser and a pencil sharpener can be helpful on these questions as they are all about accuracy
But do not erase your construction lines
Make sure your compasses aren’t loose and wobbly
They can usually be tightened with a screwdriver
Make sure you can see and read the markings on your ruler and protractor

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

