Solving Quadratic Inequalities (Edexcel GCSE Maths)
Revision Note
Solving Quadratic Inequalities
What are quadratic inequalities?
Similar to quadratic equations quadratic inequalities just mean there is a range of values that satisfy the solution
Sketching a quadratic graph is essential
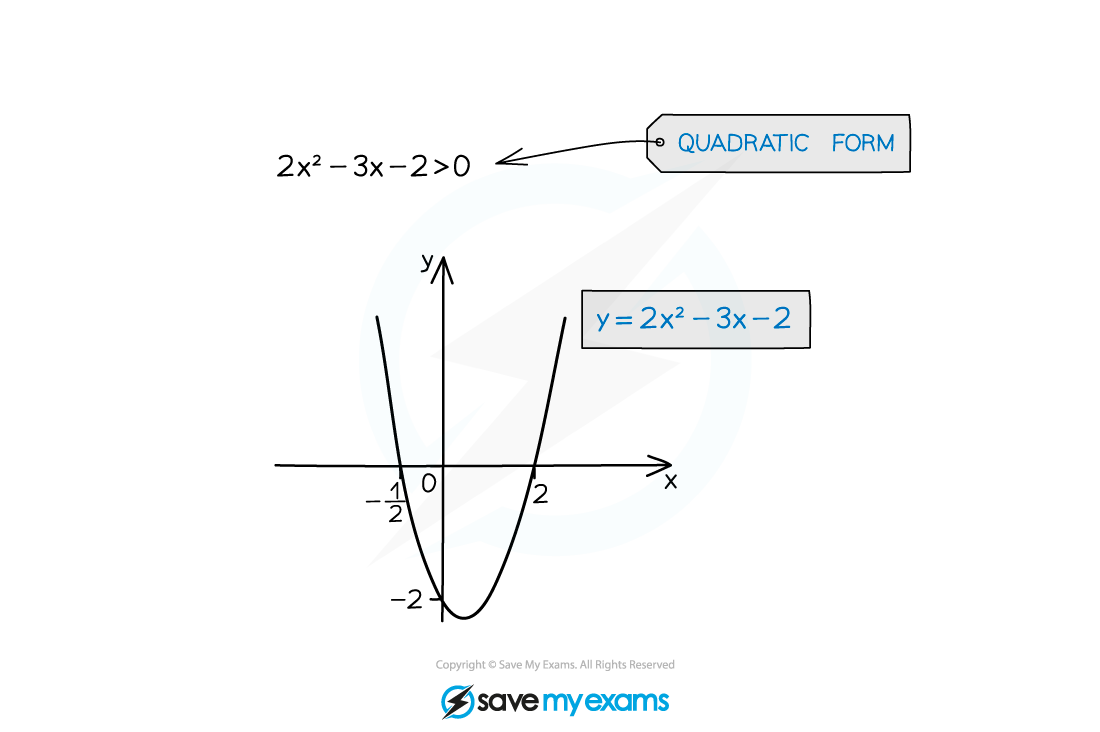
How do I solve quadratic inequalities?
STEP 1: Rearrange the inequality into quadratic form with a positive squared term
ax2 + bx + c > 0 (>, <, ≤ or ≥)
STEP 2: Find the roots of the quadratic equation
Solve ax2 + bx + c = 0 to get x1 and x2 where x1 < x2
STEP 3: Sketch a graph of the quadratic and label the roots
As the squared term is positive it will be "U" shaped
STEP 4: Identify the region that satisfies the inequality
For ax2 + bx + c > 0 you want the region above the x-axis
The solution is x < x1 or x > x2
For ax2 + bx + c < 0 you want the region below the x-axis
The solution is x > x1 and x < x2
This is more commonly written as x1 < x < x2
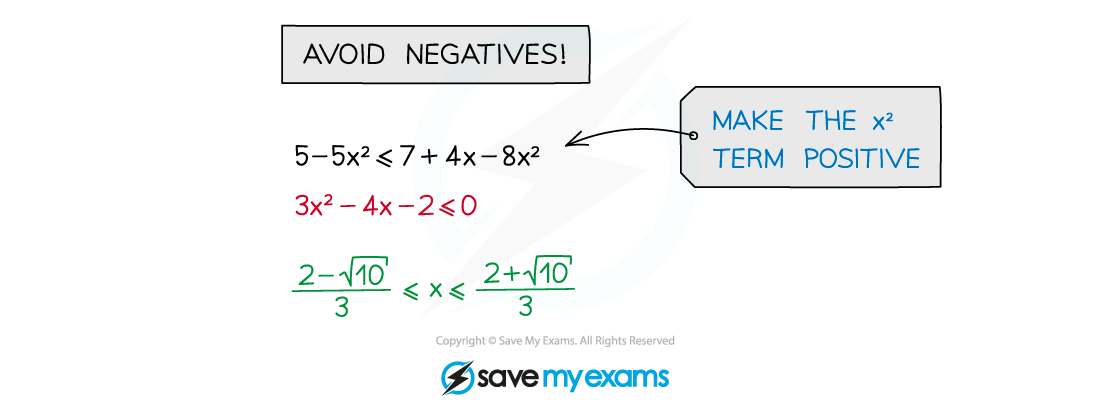
avoid multiplying or dividing by a negative number
if unavoidable, “flip” the inequality sign so < → >, ≥ → ≤, etc
avoid multiplying or dividing by a variable (x) that could be negative
(multiplying or dividing by x2 guarantees positivity (unless x could be 0) but this can create extra, invalid solutions)
do rearrange to make the x2 term positive. Be careful:
Examiner Tips and Tricks
Always start by rearranging to a quadratic with positive squared term
Always sketch a graph of the quadratic before deciding the final answer
Worked Example


You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
