Revision NotesExam QuestionsFlashcardsPast Papers
GCSEMathsEdexcelHigherRevision Notes2. AlgebraGraphs of FunctionsTypes of Graphs

Types of Graphs (Edexcel GCSE Maths)

Revision Note

Mark Curtis

Last updated

Did this video help you?

Types of Graphs

What types of graphs do I need to know?

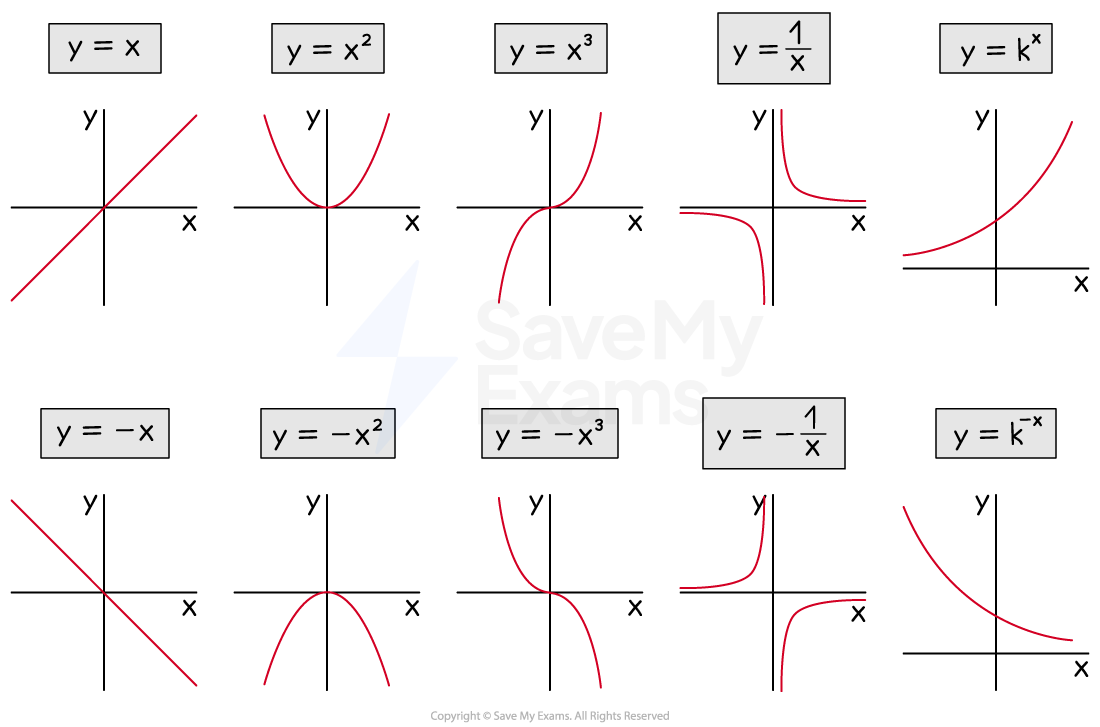
  • You need to be able to recognise, sketch, and interpret the following types of graph:

    • Linear (y equals plus-or-minus x)

      • y equals m x plus c or a x plus b y equals c

    • Quadratic (y equals plus-or-minus x squared)

      • y equals a x squared plus b x plus c

    • Cubic (y equals plus-or-minus x cubed)

      • y equals a x cubed plus b or y equals a x cubed plus b x squared plus c x

    • Reciprocal (y equals plus-or-minus 1 over x)

      • y equals a over x plus b

    • Exponential (y equals k to the power of plus-or-minus x end exponent)

      • y equals a k to the power of x plus b

Examples of linear, quadratic, cubic, reciprocal, and exponential graphs

  • You must also be able to recognise the three basic trigonometric graphs, covered in the Trigonometry section

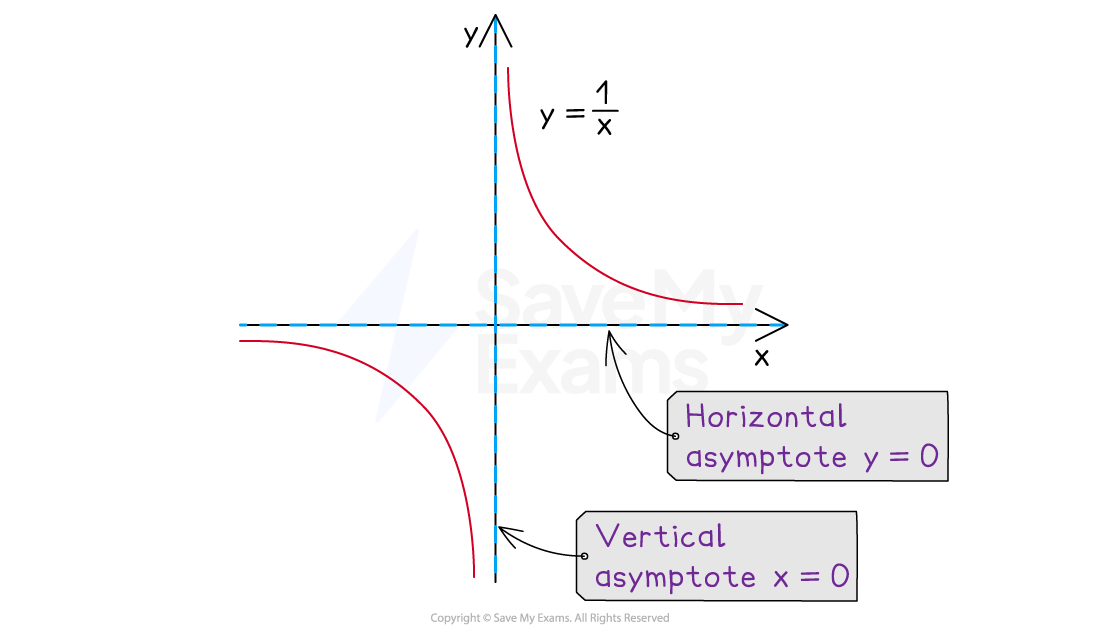
Where are the asymptotes on reciprocal graphs?

  • An asymptote is a line on a graph that a curve becomes closer to but never touches

    • These may be horizontal or vertical

  • The reciprocal graph, y equals a over x (where a is a constant)

    • does not have a y-intercept

    • and does not have any roots

  • This graph has two asymptotes

    • A horizontal asymptote at the x-axis: space y equals 0

      • This is the limiting value when the value of x gets very large (or very negative)

    • A vertical asymptote at the y-axis: space x equals 0

      • This is the value that causes the denominator to be zero

Asymptotes on the graph of 1/x

  • The reciprocal graph, y equals a over x plus b (where a and b are both constants)

    • is the same shape as y equals a over x

    • but is shifted upwards by b units

      • y equals a over x minus 3 would be y equals a over x shifted down by 3 units

    • This means the horizontal asymptote also shifts up by b units

      • The vertical asymptote remains on the y-axis

How do I draw exponential growth and decay?

  • The equation y equals k to the power of x represents exponential growth when k greater than 1

    • y equals k to the power of x represents exponential decay when 0 less than k less than 1

      • k is positive but less than 1

  • Both of these graphs:

    • have a horizontal asymptote at y equals 0

    • do not have a vertical asymptote

    • have a y-intercept of open parentheses 0 comma space 1 close parentheses

  • The graph of y equals a k to the power of x plus b is a similar shape to y equals k to the power of x, but there are some differences

    • It is first stretched vertically by a

    • It is then shifted b units upwards

      • Therefore it has a horizontal asymptote at y equals b

      • and a y-intercept of open parentheses 0 comma space a plus b close parentheses

  • For example, a population may be modelled as y equals 400 cross times open parentheses 1 half close parentheses to the power of x plus 100, where y is the population and x represents time

    • This is an exponential decay as 0 less than k less than 1

    • The initial population (when x equals 0) will be 400 + 100 = 500

      • The y-intercept is (0, 500)

    • Over a long period of time (large x-value) the population will settle to 100

      • The asymptote is at y equals 100

  • Exponential decay can also be identified by a negative power using index laws

    • open parentheses 1 half close parentheses to the power of x equals open parentheses 2 to the power of negative 1 end exponent close parentheses to the power of x equals 2 to the power of negative x end exponent so y equals 400 cross times 2 to the power of negative x end exponent plus 100 is the model above

    • This has the form y equals k to the power of negative x end exponent where k greater than 1

Worked Example

Match the graphs to the equations.

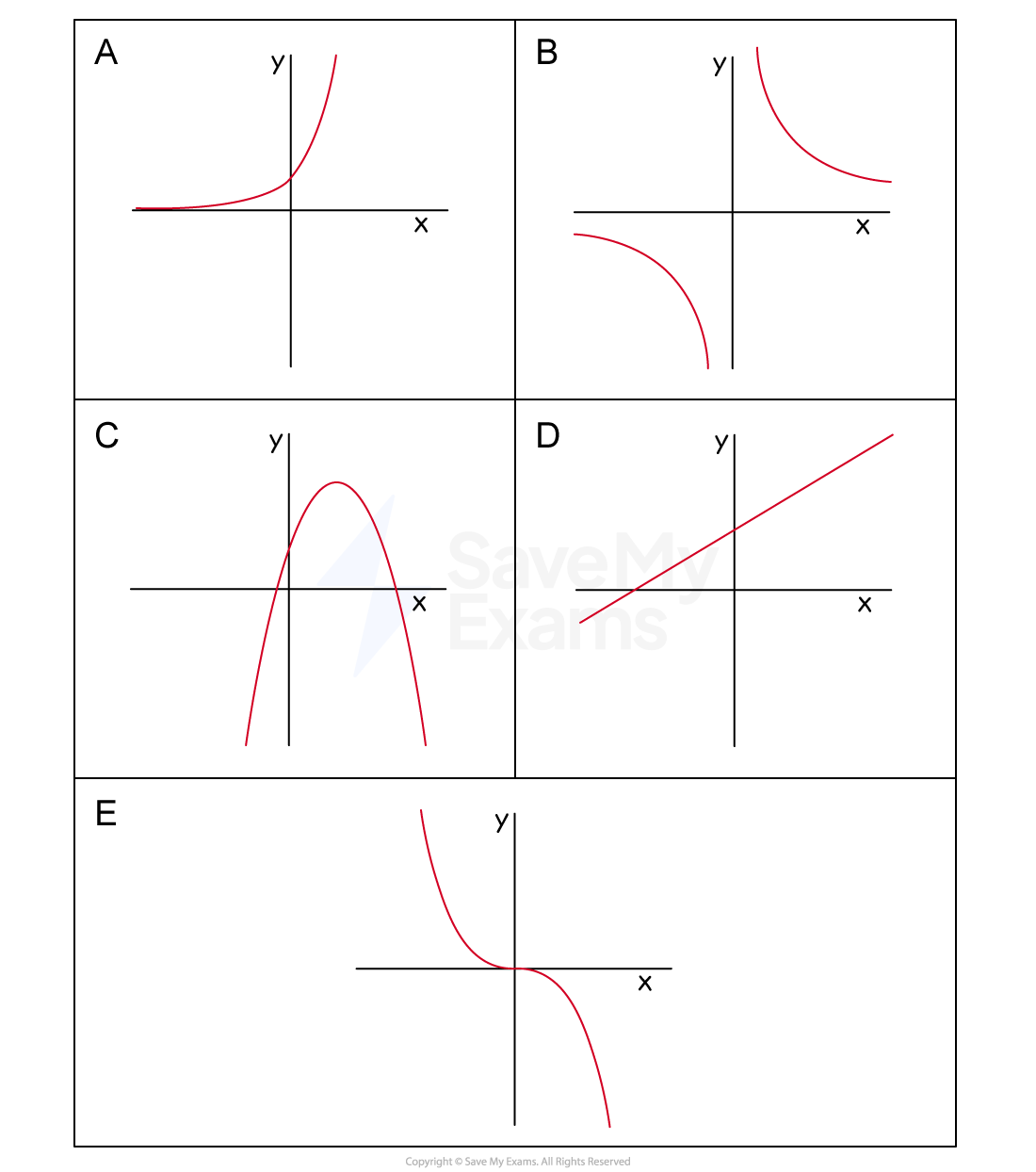
5 different shapes of graph; exponential, reciprocal, negative quadratic, linear, and negative cubic

(1) y equals 0.6 x plus 2,    (2) y equals 3 to the power of x,    (3) y equals negative 0.7 x cubed,    (4) y equals 4 over x,   (5) y equals negative x squared plus 3 x plus 2

Starting with the equations,

(1) is a linear equation (y = mx + c) so matches the only straight line, graph D

(2) is an exponential equation with a positive coefficient so matches graph A

(3) is a cubic equation with a negative coefficient so matches graph E

(4) is a reciprocal equation with a positive coefficient so matches graph B

(5) is a quadratic equation with a negative coefficient so matches graph C

Graph A → Equation 2

Graph B → Equation 4

Graph C → Equation 5

Graph D → Equation 1

Graph E → Equation 3

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Perpendicular LinesNext:Quadratic Graphs
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.