Revision NotesExam QuestionsFlashcardsPast Papers
GCSEMathsEdexcelHigherRevision Notes2. AlgebraTransformations of GraphsReflections of Graphs

Reflections of Graphs (Edexcel GCSE Maths): Revision Note

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on

Edexcel Maths: HigherAQA Maths: HigherOCR Maths: Higher

Did this video help you?

Reflections of Graphs

What are reflections of graphs?

  • Reflections of graphs are a type of transformation where the curve is reflected about one of the axes

Two graphs showing curves and their reflections. The curve is reflected in the x-axis (left) and y-axis (right).
A curve reflected in the x-axis (left) and y-axis (right)

How do I reflect graphs?

  • Let y equals straight f open parentheses x close parentheses be the equation of the original graph

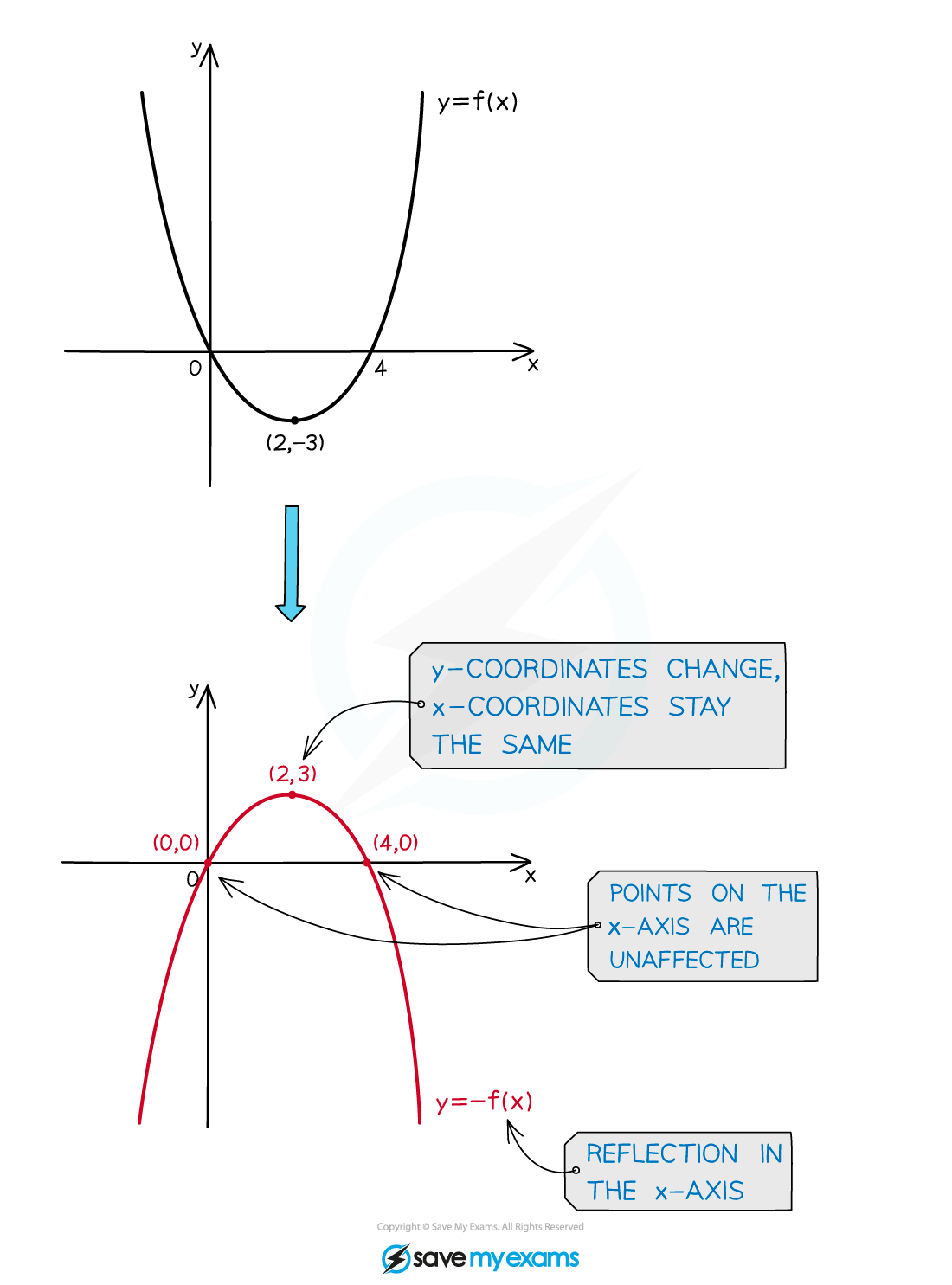
Vertical reflections: y=-f(x)

  • y equals negative straight f open parentheses x close parentheses is a reflection in the x-axis

    • The y coordinates change sign

      • The x coordinates are unaffected

Graph showing the reflection of a parabola y=f(x) in the x-axis to y=-f(x). Key points are (2,-3) reflecting to (2,3), demonstrating y-coordinate change only.

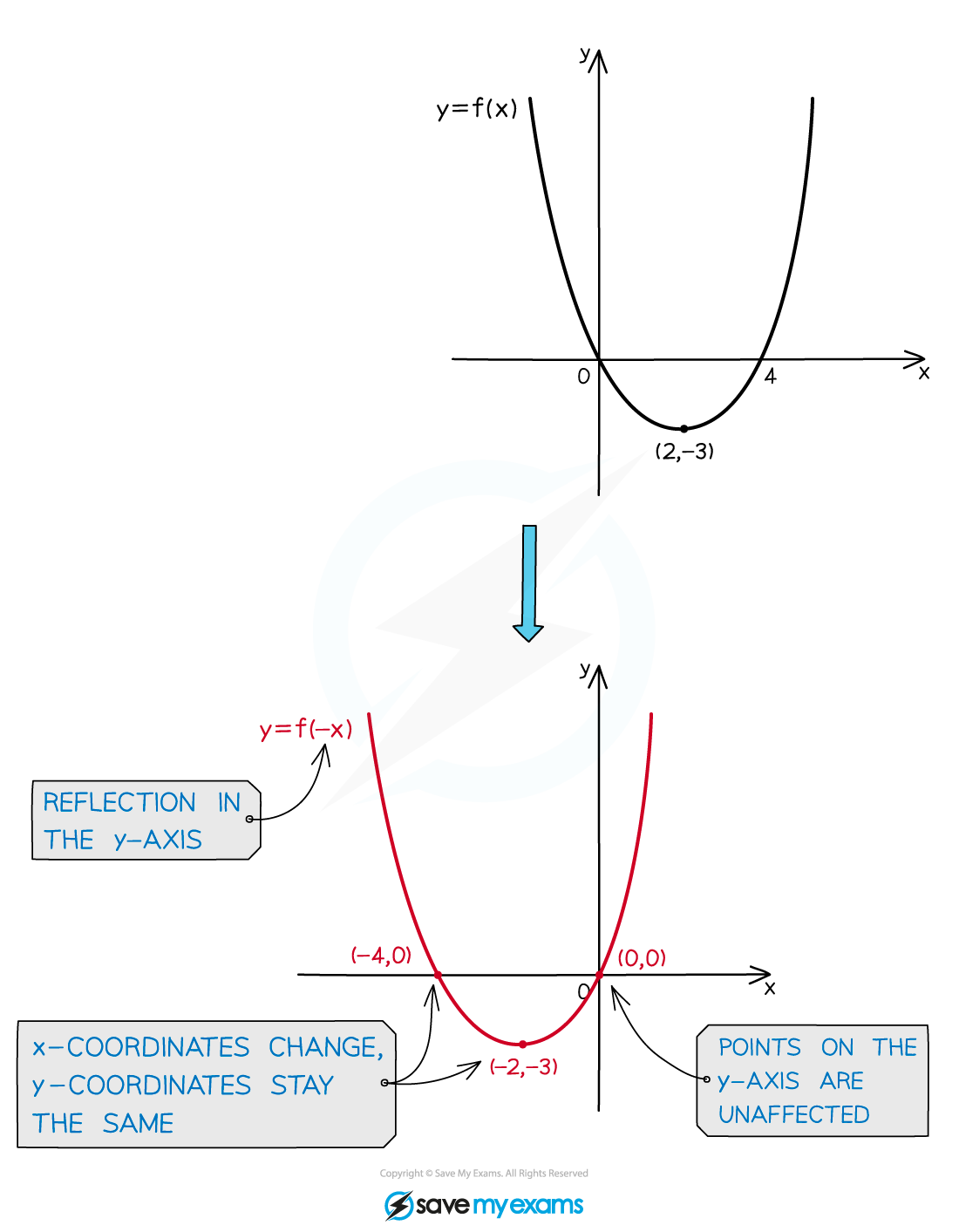
Horizontal reflections: y=f-(x)

  • y equals straight f open parentheses negative x close parentheses is a reflection in the y-axis

    • The x coordinates change sign

      • The y coordinates are unaffected

Graph showing function y=f(x) reflected in the y-axis to y=f(-x). Points on graph change x-coordinates but retain y-coordinates; points on y-axis remain affected.

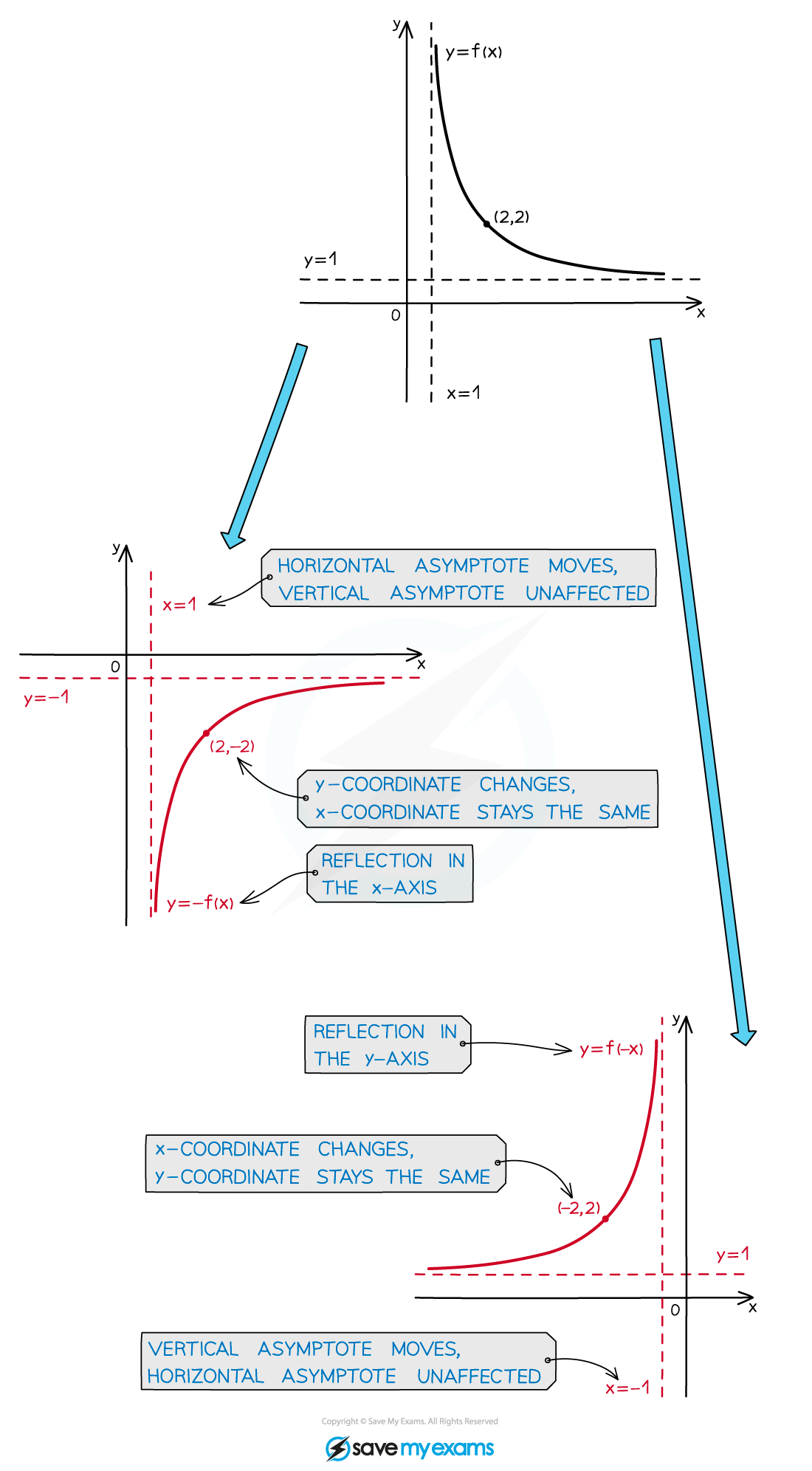
What happens to asymptotes when a graph is reflected?

  • Any asymptotes of straight f open parentheses x close parentheses are also reflected

When a graph is reflected, any asymptotes are reflected too

Examiner Tips and Tricks

When reflecting graphs in the exam, reflect any key points on the graph first, then join them up with a smooth curve.

How does a reflection affect the equation of the graph?

  • When a graph is reflected, you can change its equation algebraically

    • There is no need to sketch the graph

  • Reflecting in the x-axis puts a minus in front of the whole equation

    • For example, y equals x squared plus 2 x becomes y equals negative open parentheses x squared plus 2 x close parentheses

      • This simplifies to y equals negative x squared minus 2 x

  • Reflecting in the y-axis replaces any x with open parentheses negative x close parentheses in the equation

    • For example, y equals x squared plus 2 x becomes y equals open parentheses negative x close parentheses squared plus 2 open parentheses negative x close parentheses

      • This simplifies to y equals x squared minus 2 x

How do I apply a combined reflection?

  • The graph of y equals negative straight f open parentheses negative x close parentheses is a combined reflection in both the x and y axes

    • It does not matter which order you apply these in

      • For example, reflect about the y-axis then about the x-axis

Worked Example

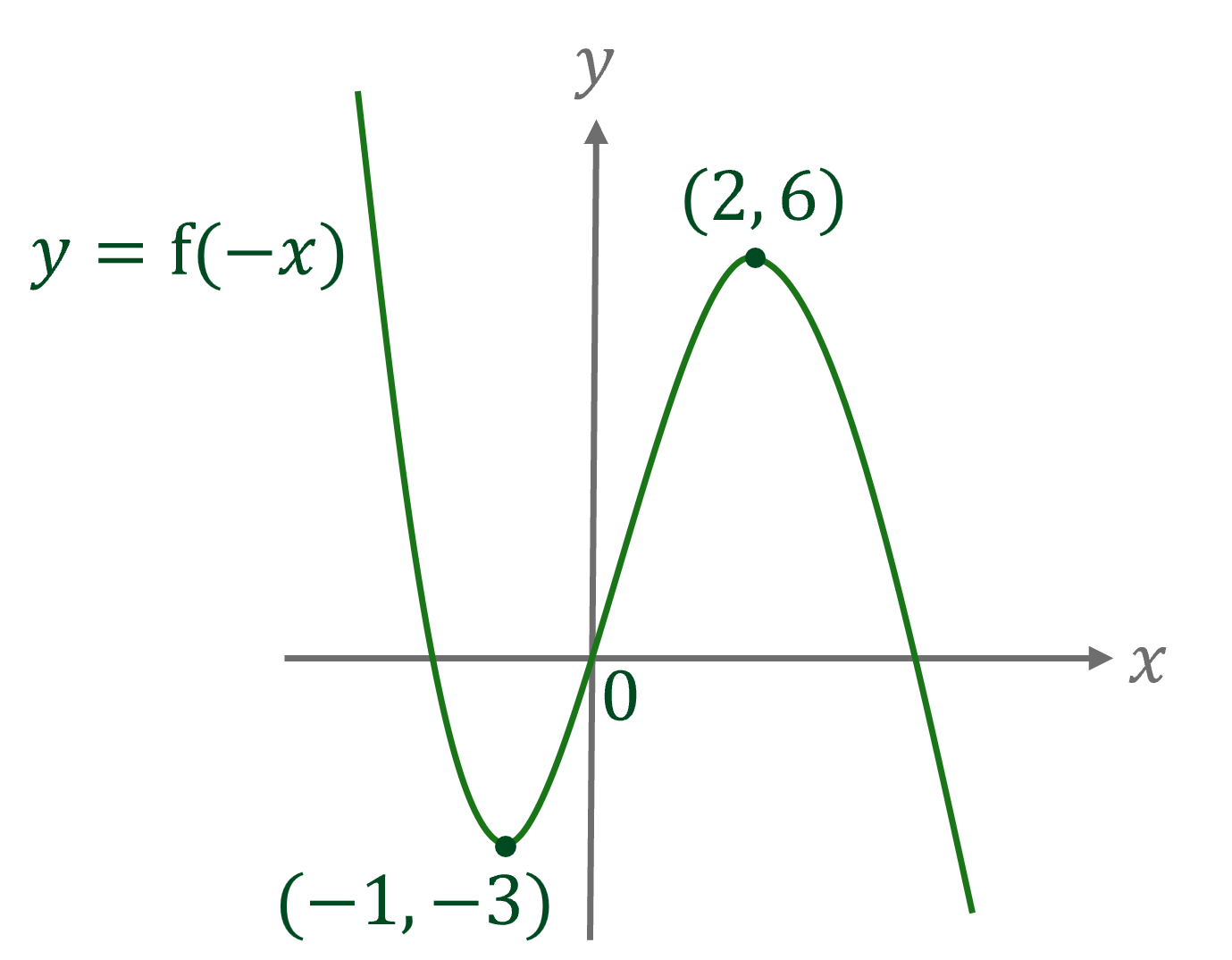
The diagram below shows the graph of y equals straight f open parentheses x close parentheses.

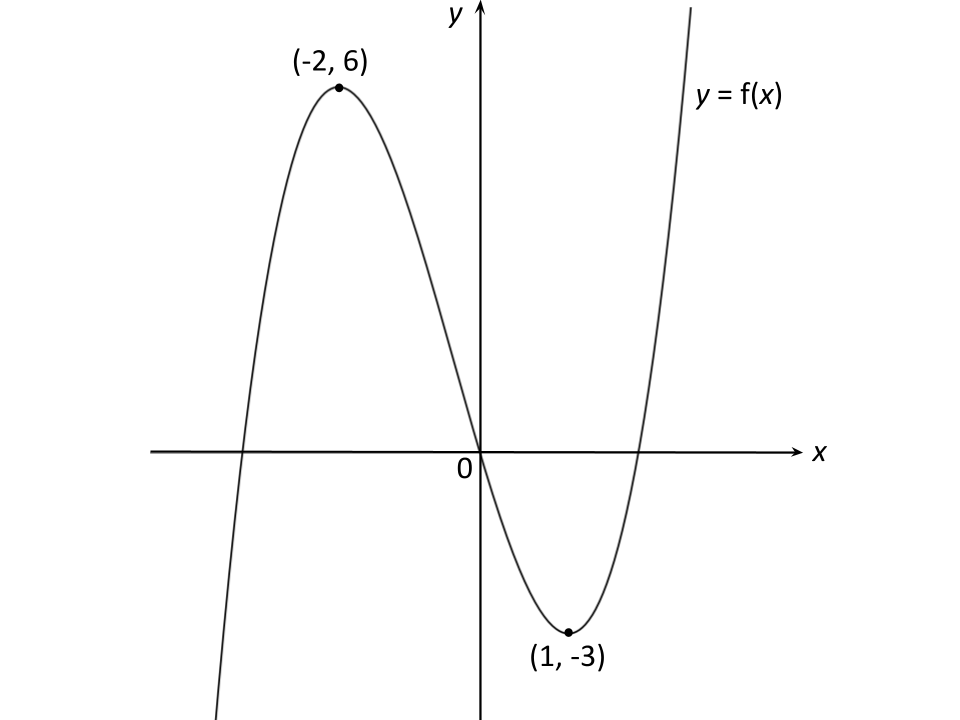
A positive cubic graph f(x)

Sketch the graph of y equals straight f open parentheses negative x close parentheses.

The transformation y equals straight f open parentheses negative x close parentheses is a reflection in the y-axis
Reflect the points (-2, 6) and (1, -3) in the y-axis to get (2, 6) and (-1, -3)
Sketch these points and join with a smooth curve through the origin

Graph of y = f(-x) showing a curve with labelled points (-1, -3) at the minimum and (2, 6) at the maximum.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Translations of GraphsNext:Introduction to Sequences
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.