Did this video help you?
Box Plots (AQA GCSE Maths)
Revision Note
Box Plots
What are box plots and when should they be used?
- Box plots are also known as box-and-whisker diagrams
- They are used when we are interested in splitting data up into quartiles
- Often, data will contain extreme values
- consider the cost of a car: there are far more family cars around than there are expensive sports cars
- if you had 50 data values about the prices of cars and 49 of them were family cars but 1 was a sports car
- the sports car’s value would not fit in with the rest of the data
- Using quartiles and drawing a box plot allows us to split the data
- we can see what is happening at the low, middle and high points
- and consider any possible extreme values
How do I draw a box plot?
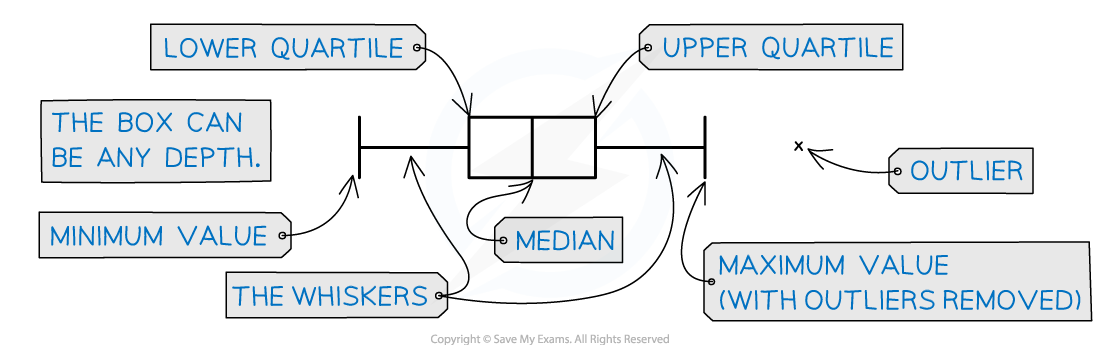
- You need to know five values to draw a box plot
- Lowest data value
- Lower quartile
- Median
- Upper quartile
- Highest data value
- Usually on graph paper, box plots are drawn accurately with the five points marked by short vertical lines
- the middle three values then form a box with the median line inside
- the median will not necessarily be in the middle of the box!
- the box represents the interquartile range (middle 50% of the data)
- the lowest data value and highest data value are joined to the box by horizontal lines
- these are often called whiskers
- they represent the lowest 25% of the data and the highest 25% of the data
- the middle three values then form a box with the median line inside
- You may be given a box plot
- from which you can read off the five values
- calculate other statistics like the range and interquartile range (IQR)
How do I compare box plots?
- If you are asked to compare box plots aim for two pairs of comments
- the first pair of comments should mention average - i.e. the median
- the first comment should compare the value of the medians
e.g. the median for boys (12) is greater than the median for girls (8) - the second comment should explain it in the context of the question
e.g. the boys were, on average, 4 seconds slower than the girls
- the first comment should compare the value of the medians
- the second pair of comments should mention spread - i.e. the interquartile range (or range)
- the first comment should compare the value of the IQRs
e.g. the IQR for boys (6) is lower than the IQR for girls (9) - the second comment should explain it in the context of the question
e.g. the boys times were less spread out than the girls, the boys were more consistent
- the first comment should compare the value of the IQRs
- the first pair of comments should mention average - i.e. the median
Worked example
The box plot below shows the number of goals scored per game by Albion Rovers during a football season.
The information below shows the number of goals score per game by Union Athletic during the same football season.
| Median number of goals per game | 4 |
| Lower quartile | 2 |
| Upper quartile | 7.5 |
| Lowest number of goals per game | 1 |
| Highest number of goals per game | 10 |
(a)
Draw a box plot for the Union Athletic data.
Draw the box plot by first plotting all five points as vertical lines.
Draw a box around the middle three and then draw whiskers out to the outer two.
(b)
Compare the number of goals scored per game by the two teams.
Your first comment should be about averages - do it in two sentences.
Your first sentence should be just about the maths and numbers involved. The second should be about what it means.
The median number of goals per game is higher for Union Athletic (4 goals) than Albion Rovers (3 goals).
This means that on average, Union Athletic scored more goals per game than Albion Rovers.
Your second comment should be about spread - do it in two sentences.
Your first sentence should be just about the maths and numbers involved. The second should be about what it means.
The interquartile range (IQR) is higher for Union Athletic (4) than Albion Rovers (3).
This means that Albion Rovers were more consistent regarding the number of goals they scored per game.
Remember a smaller range/IQR means more consistent which, depending on the situation, may be desirable.
You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?