Basic Probability (AQA GCSE Maths)

What is probability?

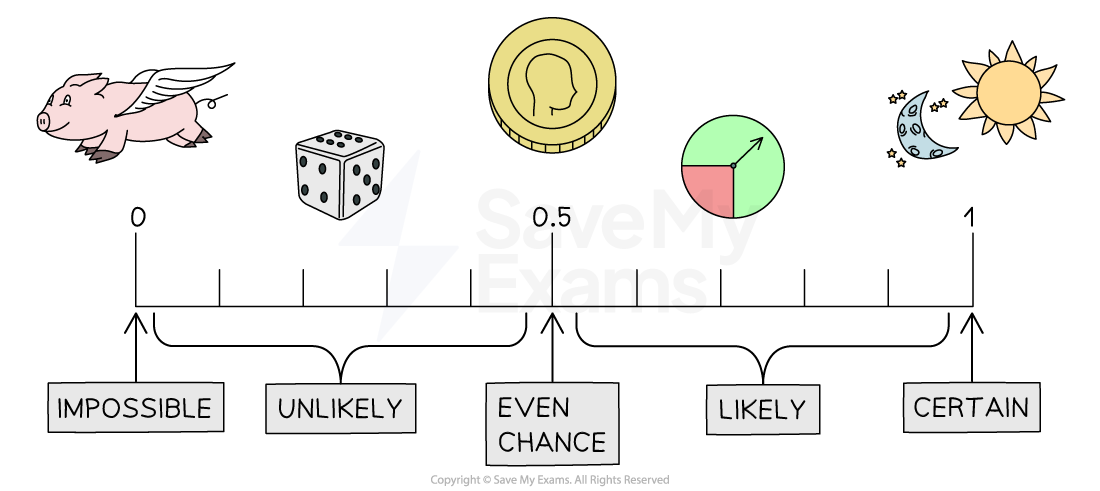
• Probability describes the likelihood of something happening
• In real-life you might use words such as impossible, unlikely, certain, etc to describe probability
• In maths we use the probability scale to describe probability
  • This means giving it a number between 0 (impossible) and 1 (certain)
  • Probabilities can be given as fractions, decimals or percentages

What key words and terminology are used with probability?

• An experiment is a repeatable activity that has a result that can be observed or recorded
  • Trials are what we call the repeats of the experiment
• An outcome is a possible result of a trial
• An event is an outcome or a collection of outcomes
  • Events are usually denoted with capital letters: A, B, etc
  • n(A) is the number of outcomes that are included in event A
  • An event can have one or more than one outcome
• A sample space is the set of all possible outcomes of an experiment
  • It can be represented as a list or a table
• The probability of event A is denoted as P(A)

How do I calculate basic probabilities?

• If all outcomes are equally likely then probability for each outcome is the same
  • Probability for each outcome is 
    • e.g. If there are 50 marbles in a bag then the probability of selecting a specific one is
• Theoretical probability of an event can be calculated without using an experiment by dividing the number of outcomes of that event by the total number of outcomes

• • Identifying all possible outcomes either as a list or a table can help
    • e.g. If there are 50 marbles in a bag and 20 of then are blue then the probability of selecting a blue marble is

How do I find missing probabilities?

• The probabilities of all the outcomes add up to 1
  • If you have a table of probabilities with one missing then you can find it by subtracting the rest from 1
• The complement of event A is the event where event A does not happen
  • This can be thought of as not A
  • This is denoted A'
    • It is always true that   

• • • This may also be written as 

What are mutually exclusive events?

• Two events are mutually exclusive if they cannot both happen at once
  • For example: when rolling a dice the events “getting a prime number” and “getting a 6” are mutually exclusive
• If A and B are mutually exclusive events then to find the probability that A or B occurs you can simply add together the probability of A and the probability of B
• Complementary events are mutually exclusive

What is a sample space?

• In probability, the sample space means all the possible outcomes
• In simple situations it can be given as a list
  • For flipping a coin, the sample space is: Heads, Tails
    • the letters H, T can be used
  • For rolling a six-sided die, the sample space is:  1, 2, 3, 4, 5, 6 
• When combining two things a grid can be used
  • For example, rolling two six-sided dice and adding their scores
  • A list of all the possibilities would be very long
    • It would be hard to spot whether you had missed any possibilities
    • It would be hard to spot any patterns in the sample space
  • Use a grid instead

• If you need to combine more than two things you'll probably need to go back to listing
  • For example, flipping three coins (or flipping one coin three times!)
    • In this case the sample space is:  HHH, HHT, HTH, THH, HTT, THT, TTH, TTT (8 possible outcomes)

How do I use a sample space to calculate probabilities?

• Probabilities can be found by counting the possibilities you want, then dividing by the total number of possibilities in the sample space
  • For example, in the sample space 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 you can count 4 prime numbers (2, 3, 5 and 7)
    • So the probability of getting a prime number is 
  • Or for rolling two dice and adding the results, the grid above shows there are 5 ways to get '8', and 36 outcomes in total
    • So the probability of getting an 8 is  
• But be careful - this counting method only works if all possibilities in the sample space are equally likely
  • For a fair six-sided die: 1, 2, 3, 4, 5, 6 are all equally likely
  • For a fair (unbiased) coin: H, T are equally likely
  • Winning the lottery: Yes, No. These are not equally likely! 
    • You cannot count possibilities here to say the probability of winning the lottery is   
• This method can also be used for finding the probability of an event occurring given that another event has occurred ('conditional probability')
  • For example when two dice are rolled, you can use the grid above to find the probability that an individual dice shows a 6, given that the total showing on the two dice is 7
    • • count the number of outcomes that sum to 7 (there are 6 of them) - this goes in the denominator
      • count the number of those outcomes in which one of the dice shows a 6 (there are two of these, (1,6) and (6,1)) - this goes in the numerator
      • So the probability is