Rotational Symmetry (AQA GCSE Maths): Revision Note
Exam code: 8300
Rotational symmetry
What is the order of rotational symmetry?
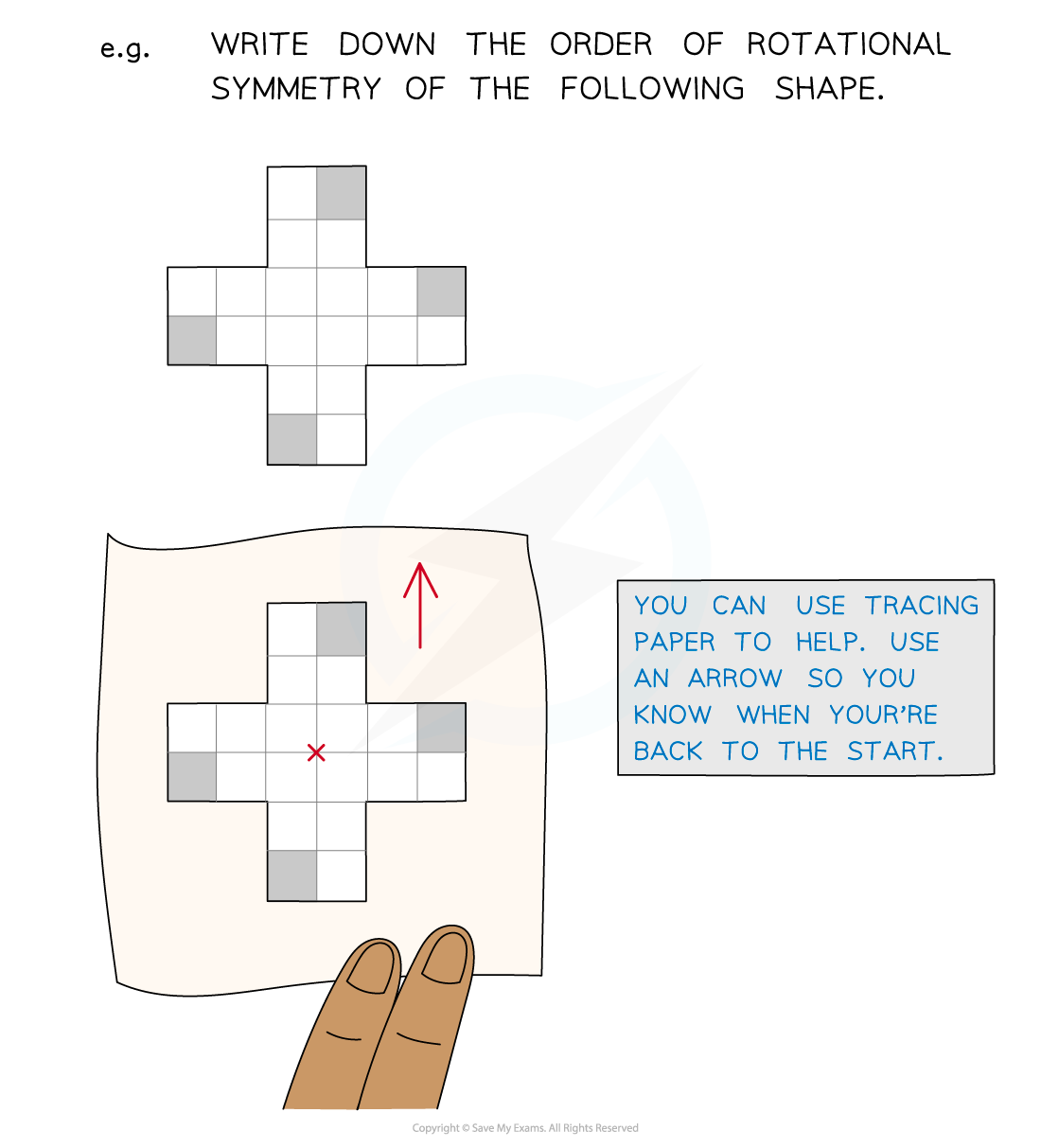
Rotational symmetry refers to the number of times a shape looks the same as it is rotated 360° about its centre
This number is called the order of rotational symmetry
Tracing paper can help work out the order of rotational symmetry
Draw an arrow on the tracing paper so you can easily tell when you have turned it through 360°
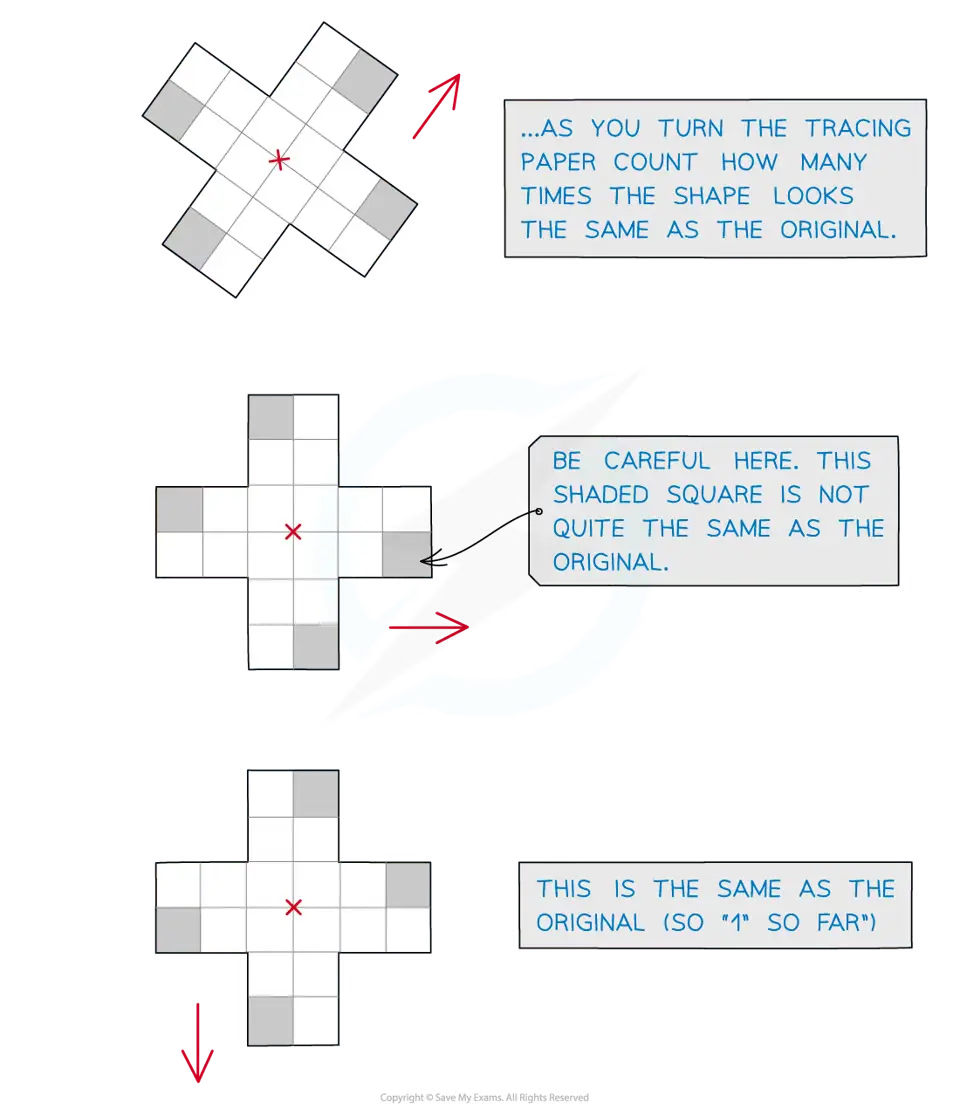
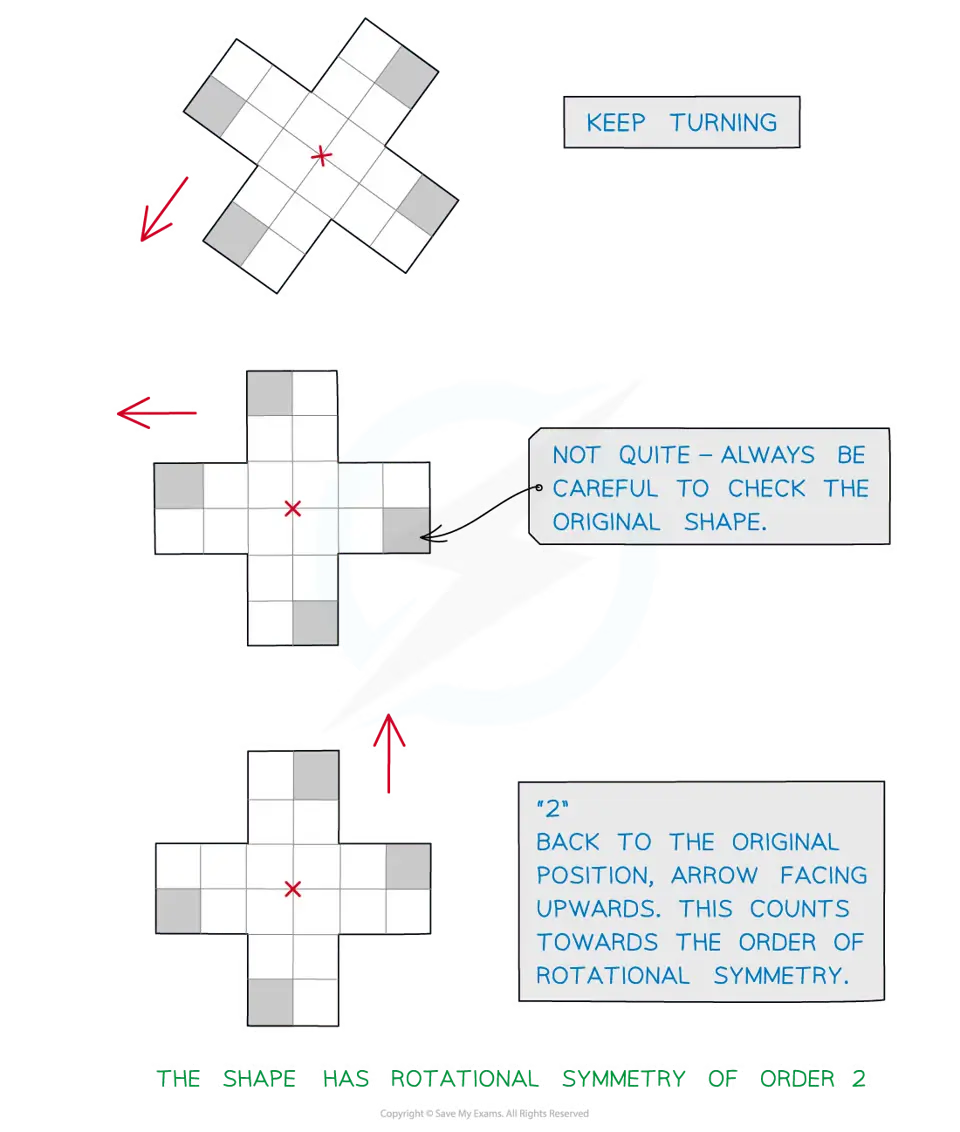
Notice that returning to the original shape contributes 1 to the order
This means a shape can never have order 0
A shape with rotational symmetry order 1 may be described as not having any rotational symmetry
The only time it looks the same is when you get back to the start
Examiner Tips and Tricks
Remember to use the trick above; using an upwards arrow on the tracing paper to show the starting orientation of the shape.
Worked Example
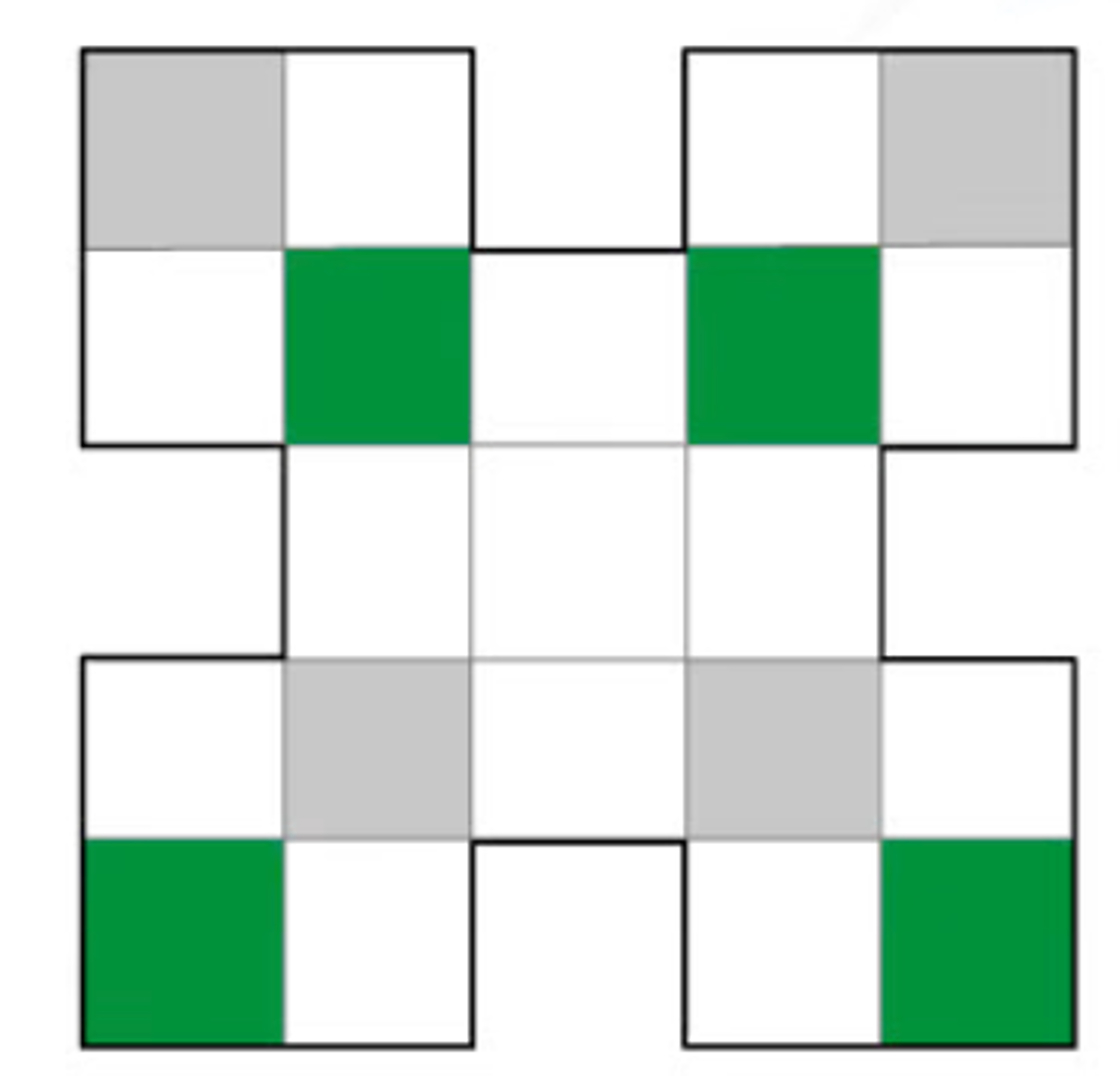
For the shape below, shade exactly 4 more squares so that the shape has rotational symmetry of order 4.
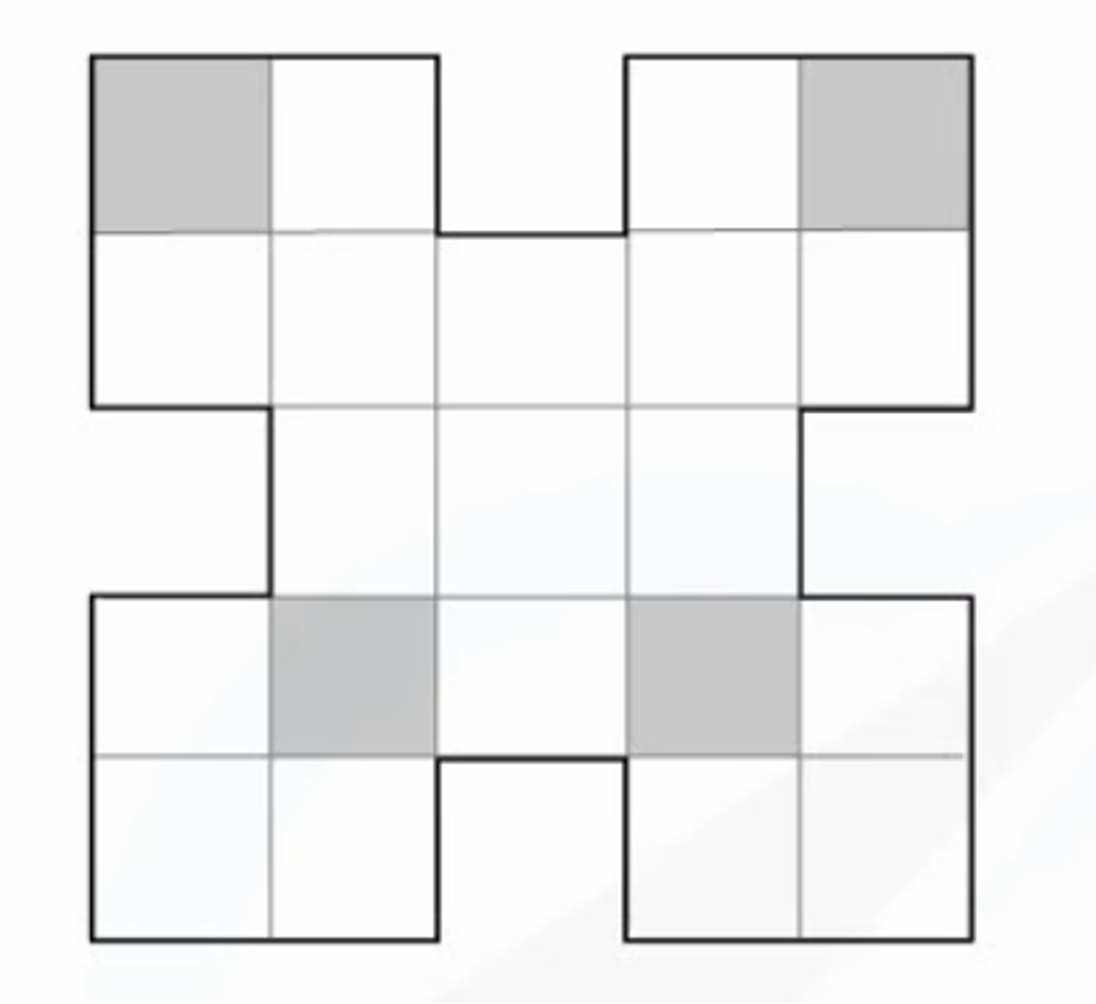
The shape below appears the same 4 times if rotated through 360 degrees

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?