Angles in Parallel Lines (AQA GCSE Maths) : Revision Note
Did this video help you?
Angles in Parallel Lines
What are parallel lines?
Parallel lines are lines that are always equidistant (the same distance apart)
No matter how far the lines are extended in either direction, they will never meet
Angles are formed when a straight line cuts through two parallel lines
What are corresponding angles in parallel lines?
Find corresponding angles by looking for an F-shape
Corresponding angles are equal

What are alternate angles in parallel lines?
Find alternate angles by looking for a Z-shape
Alternate angles are equal

What are co-interior (supplementary) angles in parallel lines?
Find co-interior angles by looking for a C-shape
Co-interior angles add up to 180°

How do I find missing angles in parallel lines?
Look for shapes that look like F, Z, or C
Vertically opposite angles can also be used in problems involving parallel lines
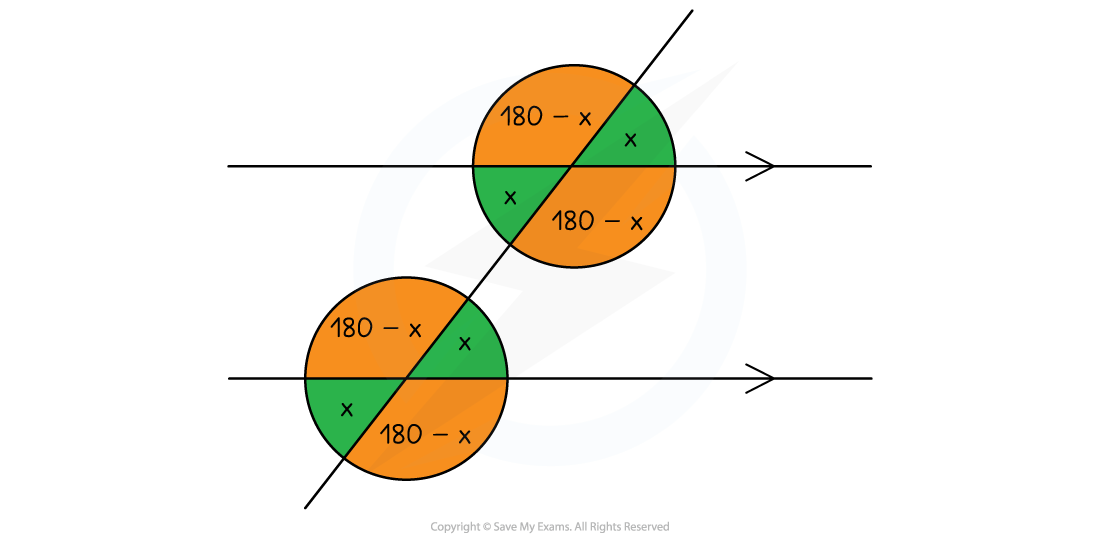
The below diagram shows how identifying angle x, can lead to knowing information about several other angles
The green angle opposite is also x, as it is vertically opposite
The orange angle must be 180-x as angles on a straight line sum to 180°
You should also be able to spot corresponding angles, alternate angles, and co-interior angles in this diagram
Examiner Tips and Tricks
Do not forget to give reasons for each step of your working in an angles question
These are often needed to get full marks
You must use the correct names as listed above
Do not use F, Z and C angles otherwise you will lose marks!
Worked Example
Find the size of the angles a and b in the diagram below.
Give a reason for each step in your working.

Vertically opposite angles are equal.
Corresponding angles on parallel lines are equal.
You must write down both of these reasons for full marks.
a = 64° (Vertically opposite angles are equal)
b = 64° (Corresponding angles on parallel lines are equal)

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

