Did this video help you?
Types of Sequences (AQA GCSE Maths)
Revision Note
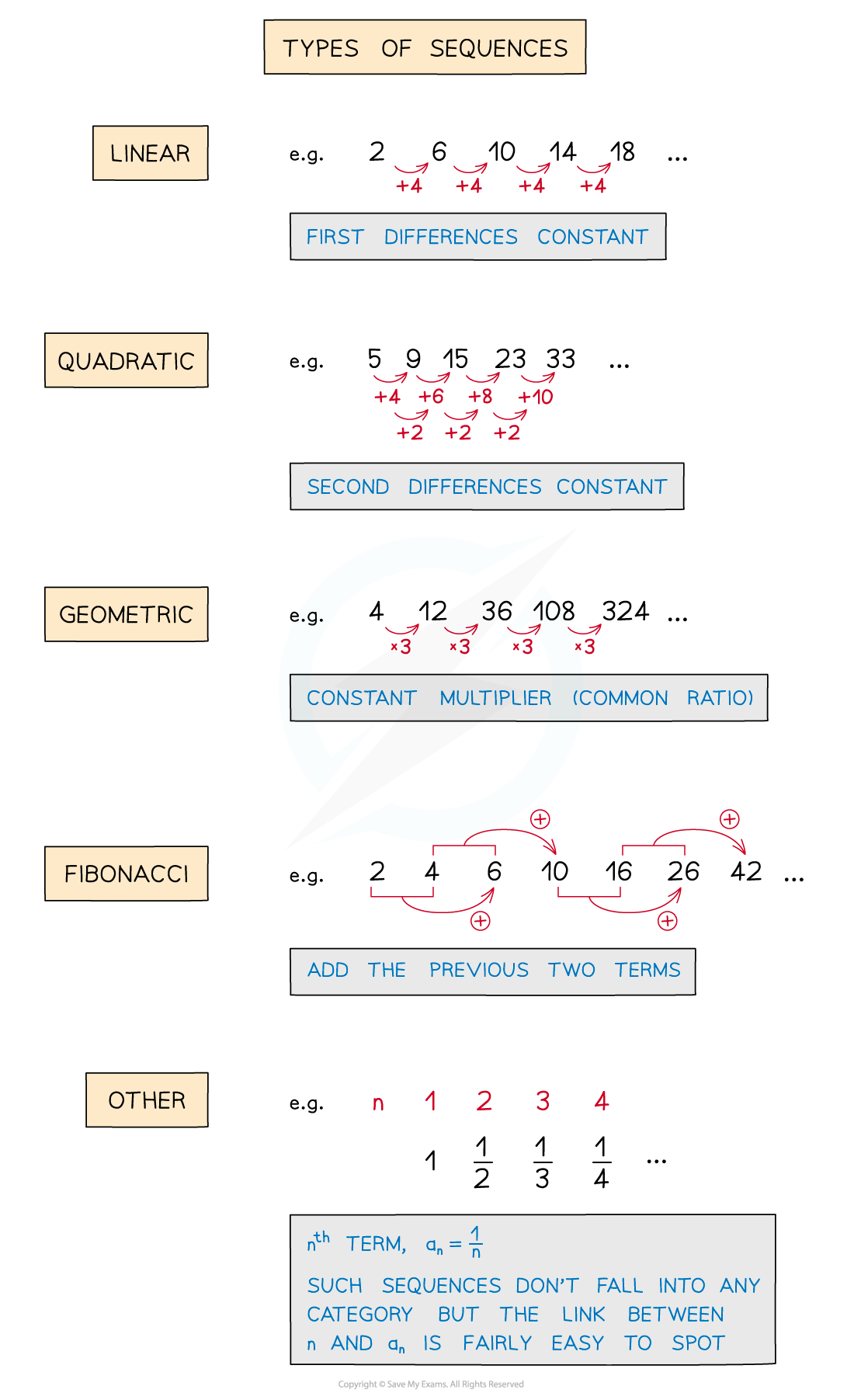
Types of Sequences
What other sequences are there?
- Linear and quadratic sequences are particular types of sequence covered in previous notes
- Other sequences include geometric and Fibonacci sequences, which are looked at in more detail below
- Other sequences include cube numbers and triangular numbers
- Another common type of sequence in exam questions, is fractions with combinations of the above
- Look for anything that makes the position-to-term and/or the term-to-term rule easy to spot
- Look for anything that makes the position-to-term and/or the term-to-term rule easy to spot
What is a geometric sequence?
- A geometric sequence can also be referred to as a geometric progression and sometimes as an exponential sequence
- In a geometric sequence, the term-to-term rule would be to multiply by a constant, r
- an+1 = r.an
- r is called the common ratio and can be found by dividing any two consecutive terms, or
- r = an+1 / an
- In the sequence 4, 8, 16, 32, 64, ... the common ratio, r, would be 2 (8 ÷ 4 or 16 ÷ 8 or 32 ÷ 16 and so on)
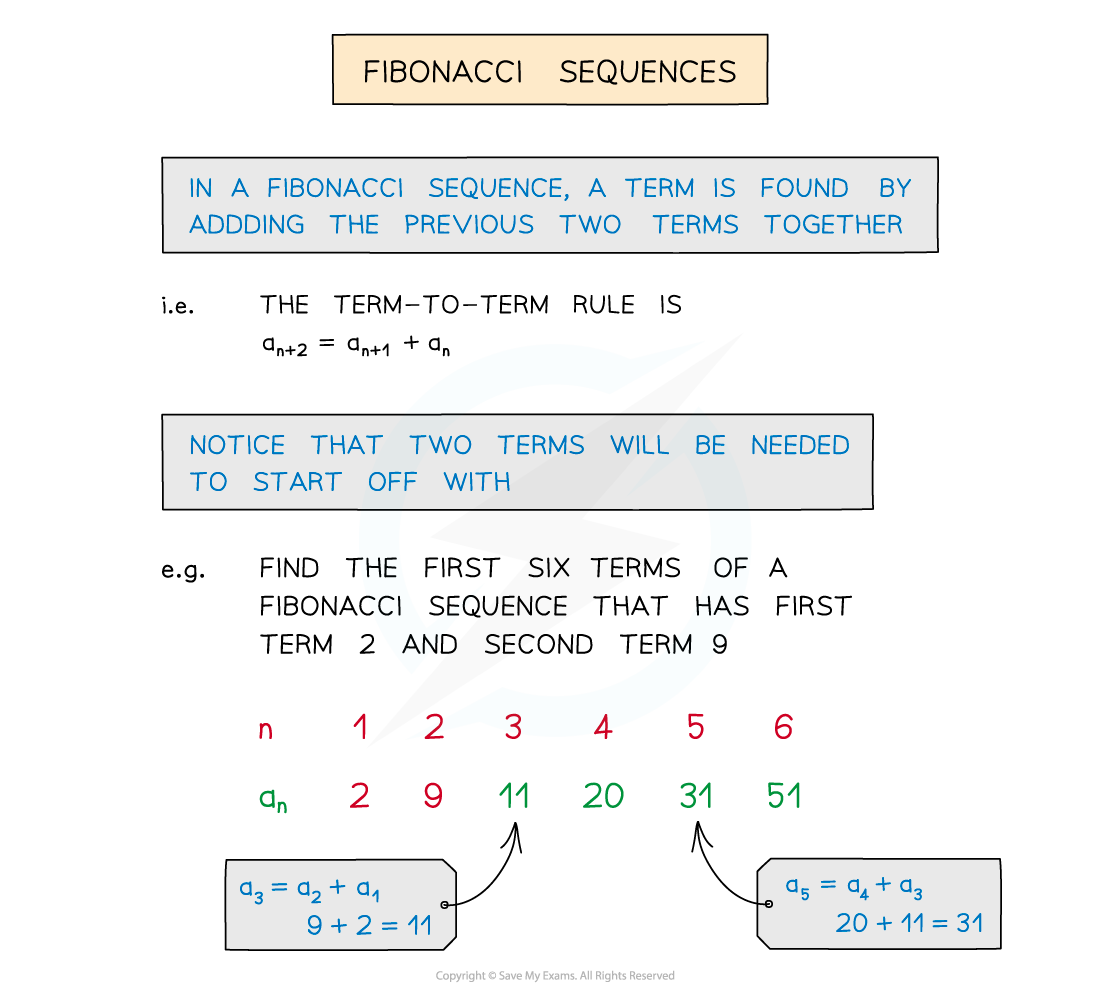
What is a Fibonacci sequence?
- THE Fibonacci sequence is 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
- The sequence starts with the first two terms as 1
- Each subsequent term is the sum of the previous two
- ie The term-to-term rule is an+2 = an+1 + an
- Notice that two terms are needed to start a Fibonacci sequence
- Any sequence that has the term-to-term rule of adding the previous two terms is called a Fibonacci sequence but the first two terms will not both be 1
- Fibonacci sequences occur a lot in nature such as the number of petals of flowers
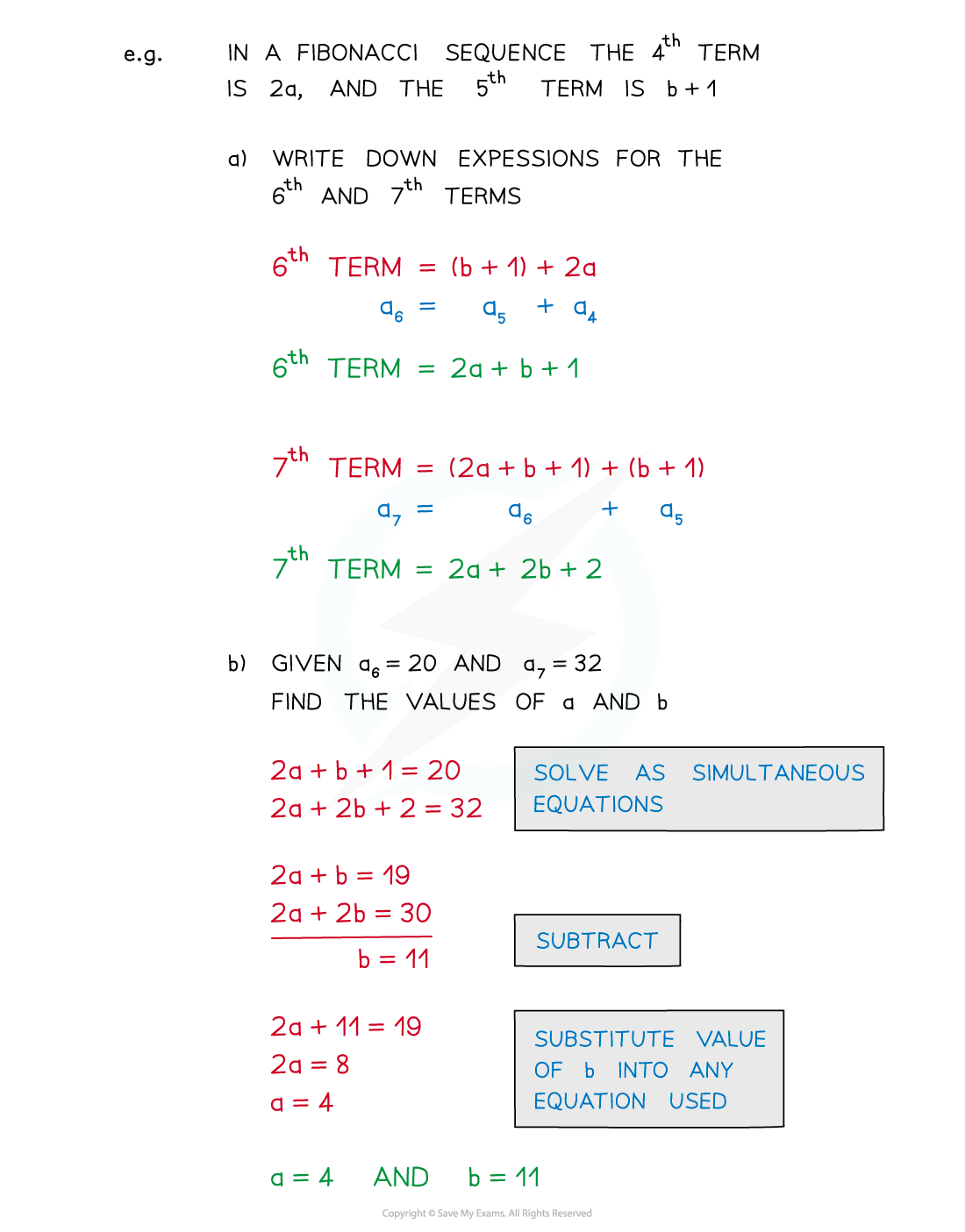
Problem solving and sequences
- When the type of sequence is known it is possible to find unknown terms within the sequence
- This can lead to problems involving setting up and solving equations
- Possibly simultaneous equations
- Other problems may involve sequences that are related to common number sequences such as square numbers, cube numbers and triangular numbers
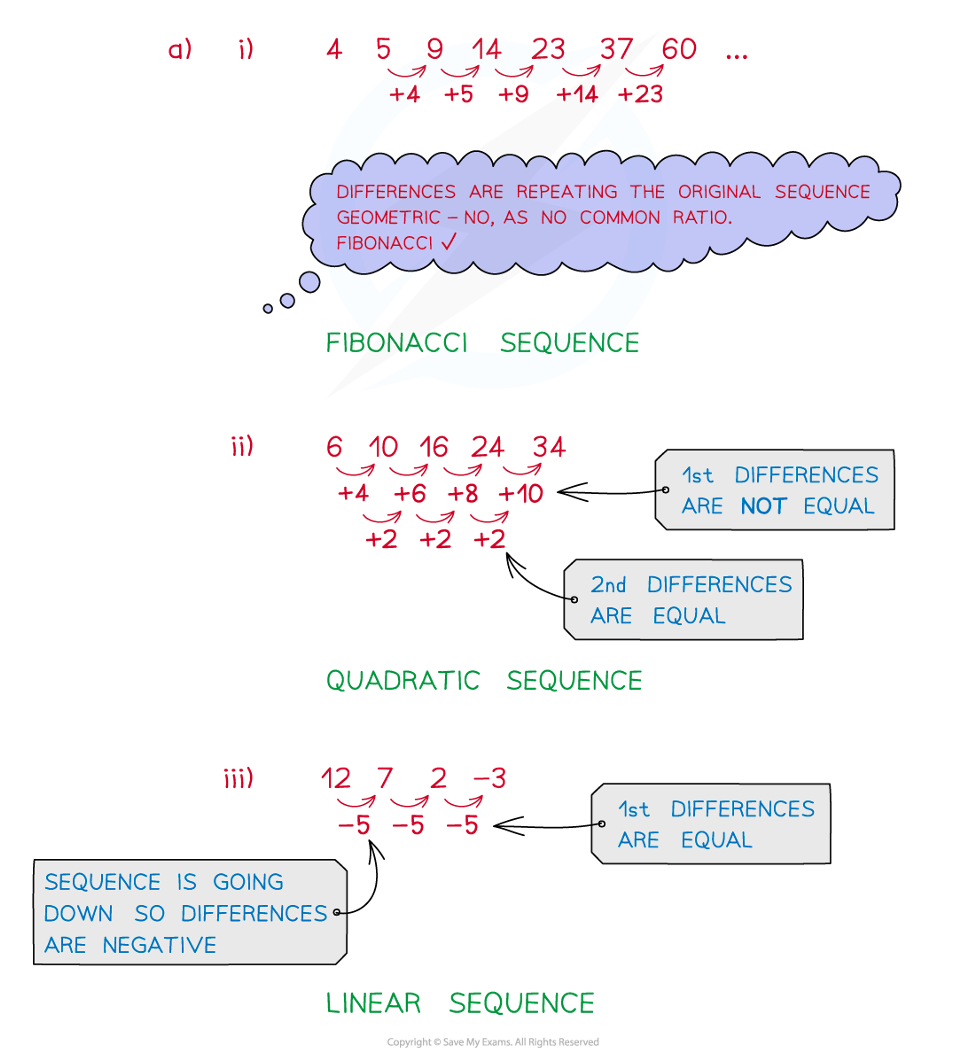
Worked example
a)
Identify the types of sequence below;
i) 4, 5, 9, 14, 23, 37, 60, ...
ii) 6, 10, 16, 24, 34, ...
iii) 12, 7, 2, -3, ...
b)
The 3rd and 6th terms in a Fibonacci sequence are 7 and 31 respectively.
Find the 1st and 2nd terms of the sequence.
You've read 0 of your 10 free revision notes
Unlock more, it's free!
Did this page help you?