Revision NotesExam QuestionsFlashcardsPast Papers
GCSEMathsAQARevision Notes2. AlgebraLinear Graphs y = mx + cStraight Line Graphs (y = mx + c)

Straight Line Graphs (y = mx + c) (AQA GCSE Maths)

Revision Note

Daniel I

Author

Daniel I

Last updated

Did this video help you?

Finding Equations of Straight Lines

Why do we want to know about straight lines and their equations?

  • Straight Line Graphs (Linear Graphs) have lots of uses in mathematics – one use is in navigation
  • We may want to know the equation of a straight line so we can program it into a computer that will plot the line on a screen, along with several others, to make shapes and graphics

How do we find the equation of a straight line?

  • The general equation of a straight line is bold italic y bold equals bold italic m bold italic x bold plus bold italic c where;
    • bold italic m is the gradient,
    • bold italic c is the y-axis intercept (or simply, the y-intercept)
  • To find the equation of a straight line you need TWO things:
    1. the gradient, m, which you can put straight into y equals m x plus c
      • get this from the question directly, or from two points using rise over run or the gradient formula 
    2. any point on the line- substitute this point into y equals m x plus c (as you already know m) and solve to find c
      • if given two points which you used to find the gradient, just choose either one of them for the point to find c
  • You may be asked to give the equation in the form a x plus b y plus c equals 0

    (especially if m is a fraction)

    If in doubt, SKETCH IT!

What if the line is not in the form y=mx+c?

  • A line could be given in the form a x plus b y plus c equals 0
    • It is harder to identify the gradient and intercept in this form
  • We can rearrange the equation into y equals m x plus c, so it is easier to identify the gradient and intercept
      • a x plus b y plus c equals 0
    • Subtract a x from both sides
      • b y plus c equals negative a x
    • Subtract c from both sides
      • b y equals negative a x minus c
    • Divide both sides by b
      • y equals negative fraction numerator a x over denominator c end fraction minus c over b
      • y equals negative a over c x minus c over b
    • In this case, the gradient is negative a over c and the y-intercept is negative c over b

Worked example

(a)

Find the equation of the straight line with gradient 3 that passes through (5, 4).


We know that the gradient is 3 so the line takes the form 

y equals 3 x plus c

To find the value of c, substitute (5, 4) into the equation


4 equals 3 open parentheses 5 close parentheses plus c 4 equals 15 plus c c equals negative 11


Replace c with −11 to complete the equation of the line

y = 3x − 11

(b)
Find the equation of the straight line that passes through (-2, 6) and (8, 1).

You may find it helpful to sketch the information given
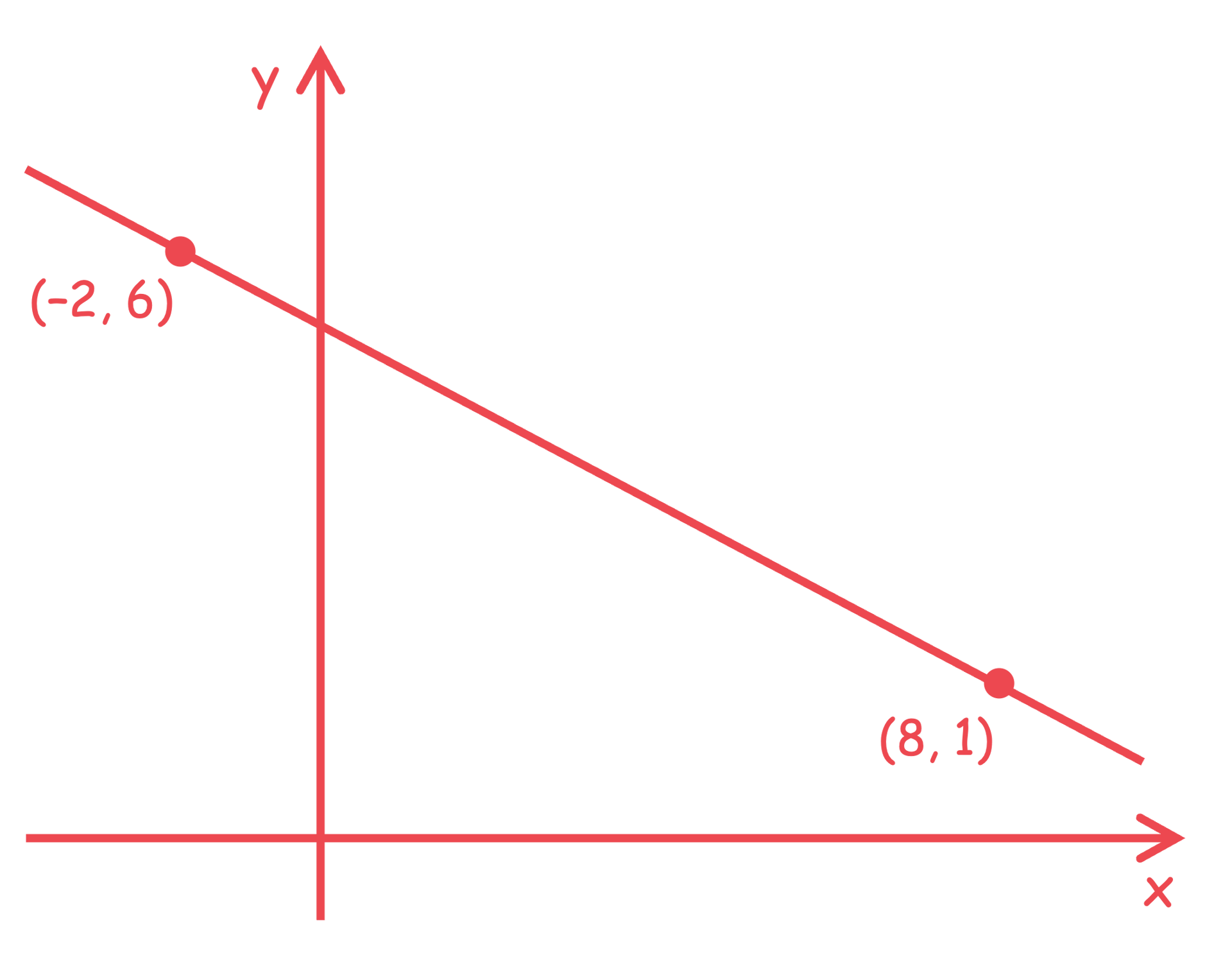
XXg8k5ry_2-13-1-finding-equations-of-straight-lines
First find m, the gradient
table row m equals cell fraction numerator 6 minus 1 over denominator negative 2 minus 8 end fraction end cell row blank equals cell fraction numerator 5 over denominator negative 10 end fraction end cell row blank equals cell negative 1 half end cell end table
We know that the line takes the form 
table row y equals cell negative 1 half x plus c end cell end table

To find the value of c, substitute either of the given points into this equation. Here we will pick (8, 1) as it is doesn't contain negative numbers so is easier to work with


1 equals negative 1 half open parentheses 8 close parentheses plus c 1 equals negative 4 plus c c equals 5


Replace c with −11 to complete the equation of the line

bold italic y bold equals bold minus bold 1 over bold 2 bold italic x bold plus bold 5

We can check against our sketch that this equation looks correct- it has a negative gradient and it crosses the y-axis between 1 and 6

Did this video help you?

Drawing Linear Graphs

How do we draw the graph of a straight line from an equation?

  • Before you start trying to draw a straight line, make sure you understand how to find the equation of a straight line – that will help you understand this
  • How we draw a straight line depends on what form the equation is given in
  • There are two main forms you might see:

    y = mx + c and ax + by = c

  • Different ways of drawing the graph of a straight line:

  1. From the form y = mx + c

    (you might be able to rearrange to this form easily)

    plot c on the y-axis

    go 1 across, m up (and repeat until you can draw the line)
  2. From ax + by = c

    put x = 0 to find y-axis intercept

    put y = 0 to find x-axis intercept

    (You may prefer to rearrange to y = mx + c and use above method)

Examiner Tip

  • It might be easier just to plot ANY two points on the line (a third one as a check is not a bad idea either)
  • or use the TABLE function on your calculator.

Worked example

On the axes below, draw the graphs of y equals 3 x minus 1 and 3 x plus 5 y equals 15.


For y equals 3 x minus 1, first plot c, which is (0, −1)

Then, as m = 3, rise over run equals 3 over 1. So plot a point 3 up and 1 right. Repeat at least once more and then join the points with a straight line. Extend the line to the edges of the grid.

y=3x-1 and 3x+5y=15, IGCSE & GCSE Maths revision notesThe steps for 3 x plus 5 y equals 15 are the same, but first we need to rearrange into the form y = mx + c

table attributes columnalign right center left columnspacing 0px end attributes row cell 5 y end cell equals cell negative 3 x plus 15 end cell row y equals cell negative 3 over 5 x plus 3 end cell end table

Now we can plot c, which is (0, 3)

For the gradient, rise over run equals fraction numerator negative 3 over denominator 5 end fraction. So plot a point 3 down and 5 right. There isn't space on the grid to repeat this so join the points with a straight line. Extend the line to the edges of the grid. The answer is shown above

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Coordinate GeometryNext:Parallel & Perpendicular Lines
    Daniel I

    Author: Daniel I

    Expertise: Maths

    Daniel has taught maths for over 10 years in a variety of settings, covering GCSE, IGCSE, A-level and IB. The more he taught maths, the more he appreciated its beauty. He loves breaking tricky topics down into a way they can be easily understood by students, and creating resources that help to do this.