Volume (AQA GCSE Maths) : Revision Note
Did this video help you?
Volume
What is volume?
The volume of a 3D shape is a measure of how much space it takes up
You need to be able to calculate the volumes of a number of common 3D shapes, including:
Cubes and cuboids
Prisms
Pyramids
Cylinders
Spheres
How do I find the volume of a cube or a cuboid?
A cube is a special cuboid, where the length, width and height are all of equal length
A cuboid is another name for a rectangular-based prism
To find the volume, V, of a cube or a cuboid, with length, l, width, w, and height, h, use the formula
This formula is not given to you in the exam
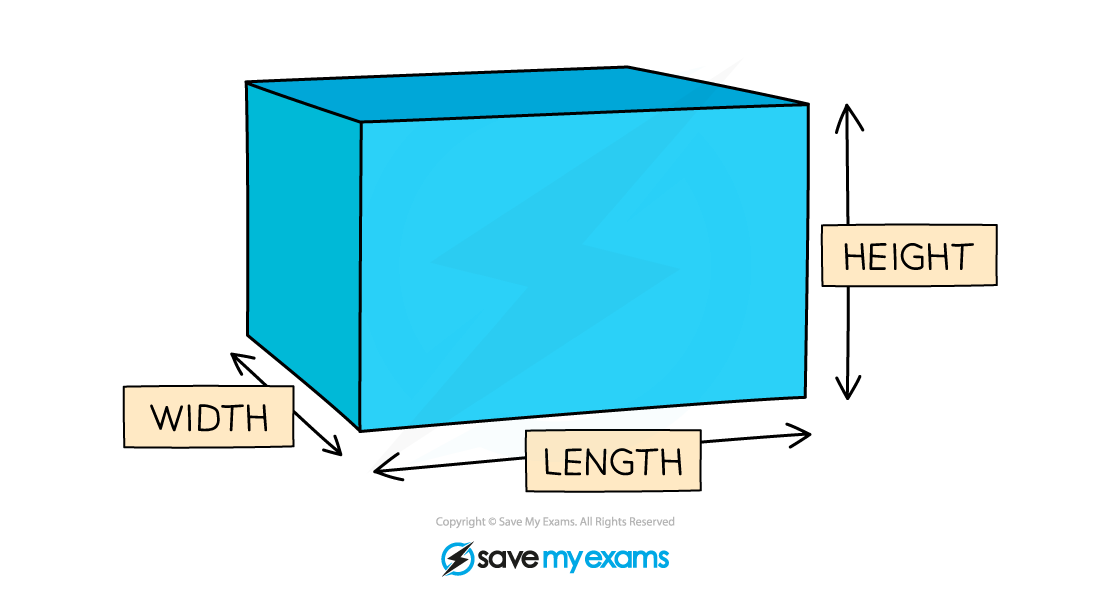
You will sometimes see the terms 'depth' or 'breadth' instead of 'height' or 'width'
How do I find the volume of a prism?
A prism is a 3D object with a constant cross-sectional area
To find the volume, V, of a prism, with cross-sectional area, A, and length, l, use the formula
This formula is not given to you in the exam
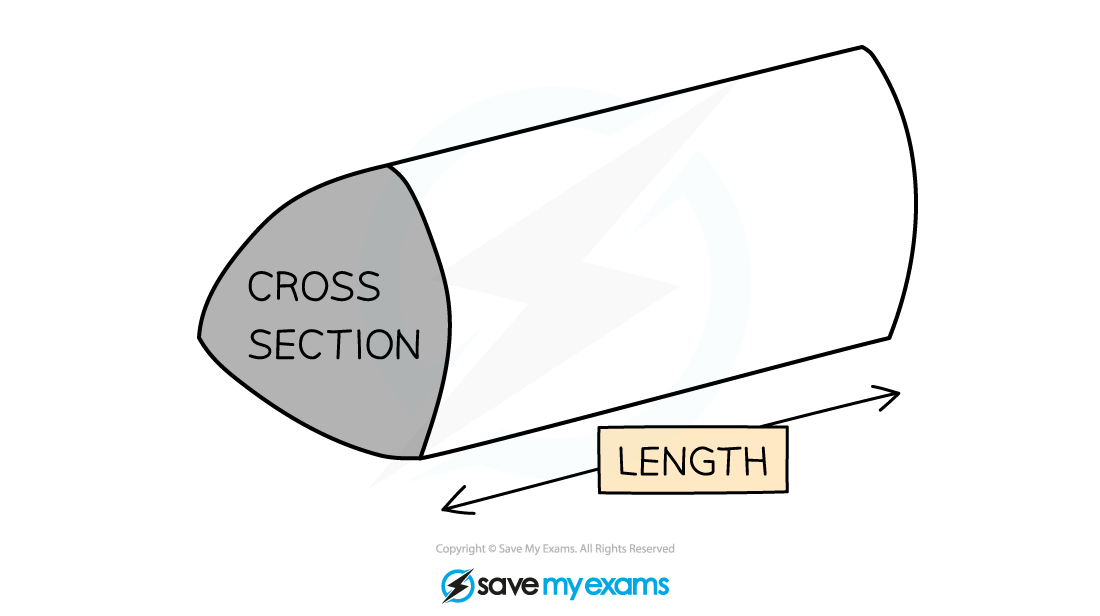
Note that the cross-section can be any shape, so as long as you know its area and the length of the prism, you can calculate its volume
If you know the volume and length of the prism, you can calculate the area of the cross-section
How do I find the volume of a cylinder?
To calculate the volume, V, of a cylinder with radius, r, and height, h, use the formula
This formula is not given to you in the exam
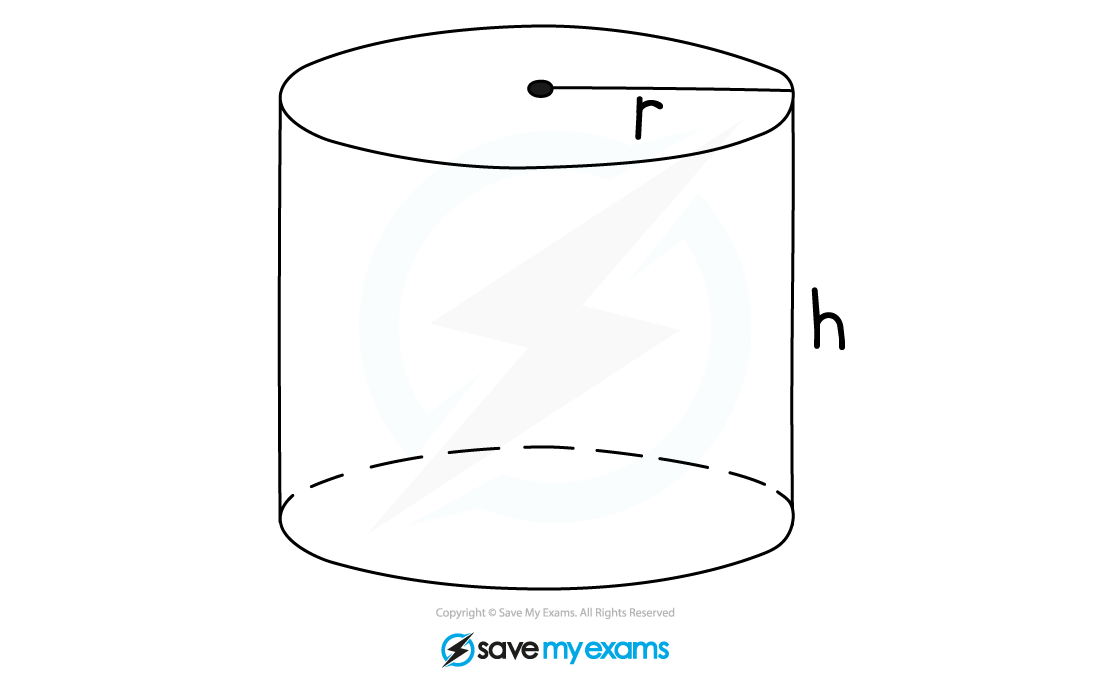
Note that a cylinder is similar to a prism, its cross-section is a circle with area
, and its length is h
How do I find the volume of a pyramid?
To calculate the volume, V, of a pyramid with base area, A, and perpendicular height, h, use the formula
This formula is not given to you in the exam
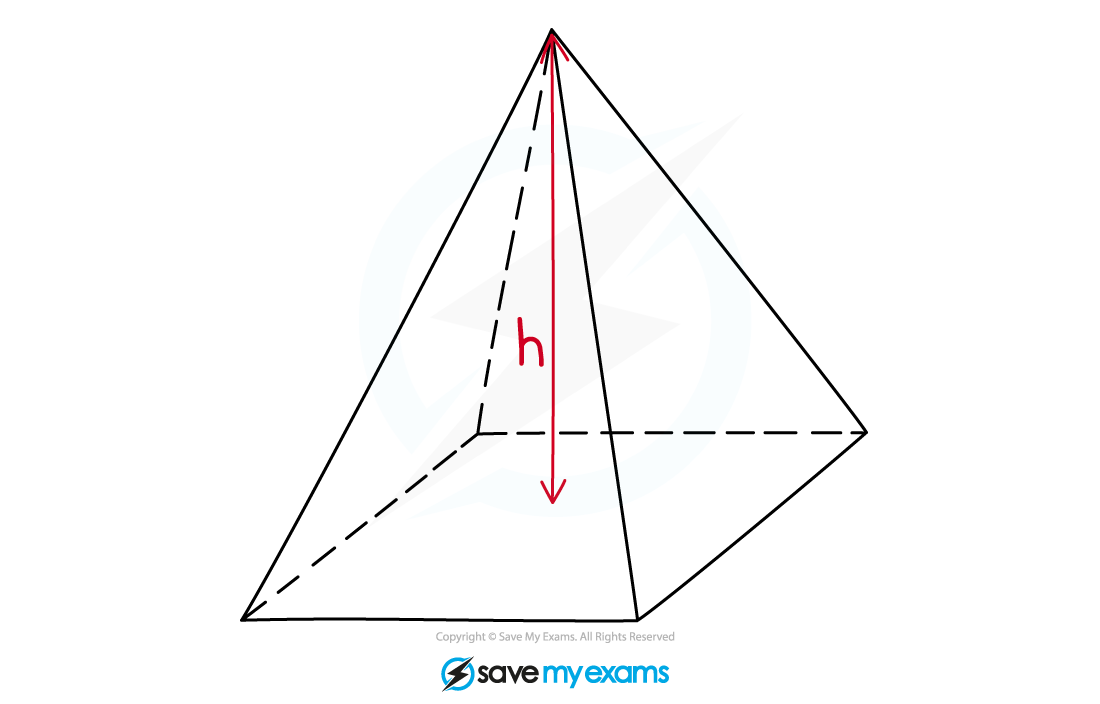
The height must be a line from the top of the pyramid that is perpendicular to the base
The base of a pyramid could be a square, a rectangle or a triangle
How do I find the volume of a cone?
To calculate the volume, V, of a cone with base radius, r, and perpendicular height, h, use the formula
This formula is given to you in the exam
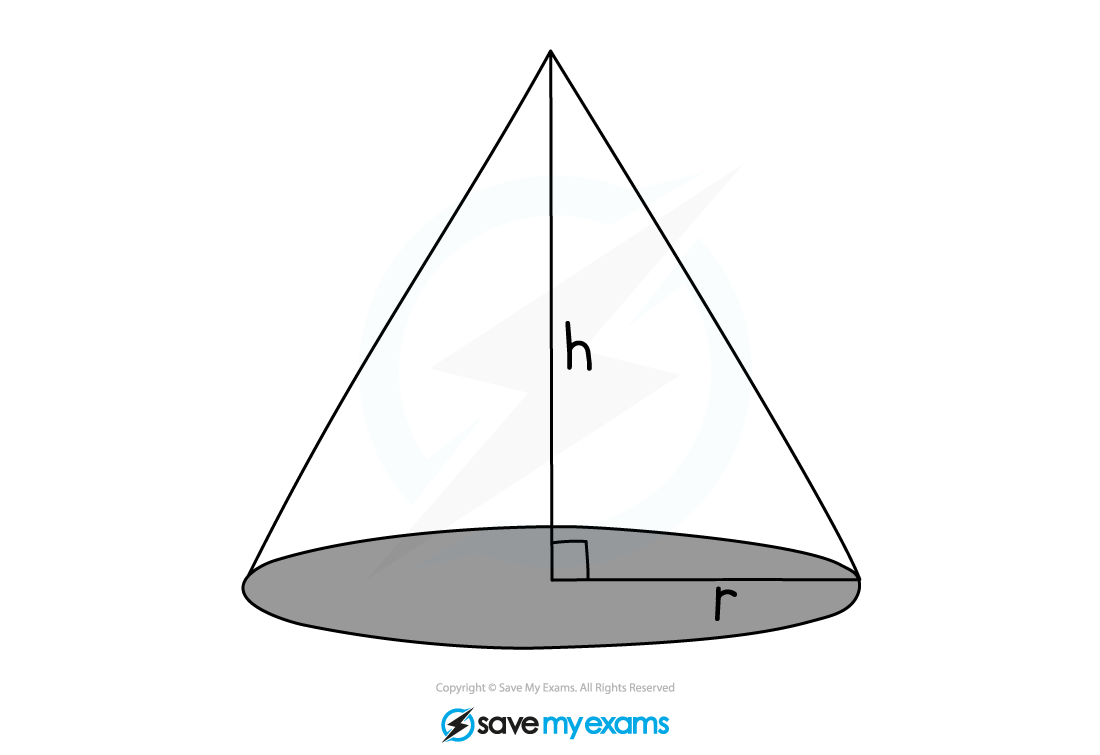
Note that volume formula for a cone is similar to a pyramid
The height must be a line from the top of the cone that is perpendicular to the base
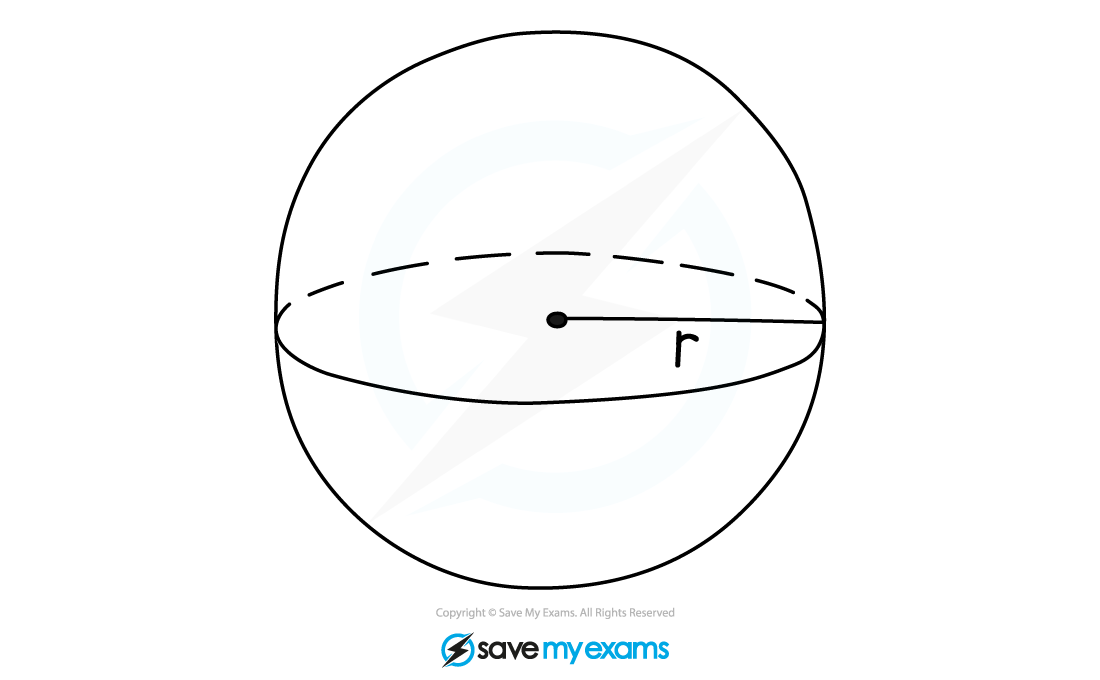
How do I find the volume of a sphere?
To calculate the volume, V, of a sphere with radius, r, use the formula
This formula is given to you in your exam
Examiner Tips and Tricks
You only need to memorise the volume formulae for cuboids!
Worked Example
A cylinder is shown.
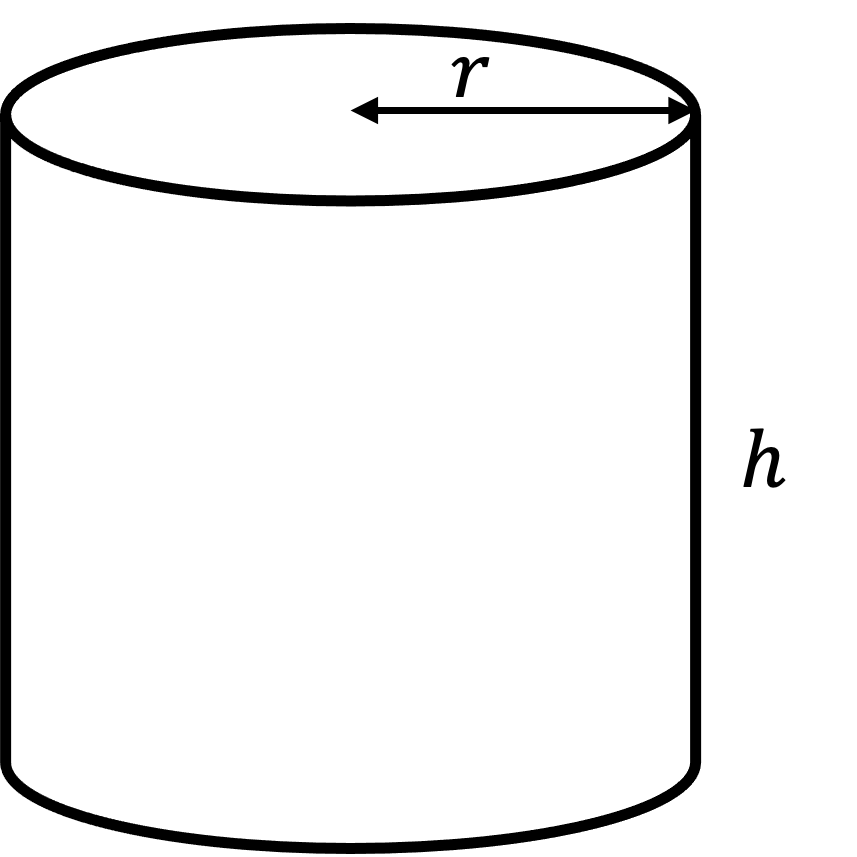
The radius, r, is 8 cm and the height, h, is 20 cm.
Calculate the volume of the cylinder, giving your answer correct to 3 significant figures.
A cylinder is similar to a prism but with a circular base
The volume of any prism, V, is its base area × height, h, where the base area here is for a circle,
Substitute r = 8 and h = 20 into the formula
Work out this value on a calculator
4021.238...
Round the answer to 3 significant figures
4020 cm3

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
