Revision NotesExam QuestionsFlashcardsPast Papers
GCSEMathsAQAHigherRevision Notes4. Geometry & MeasuresVolume & Surface AreaProblem Solving with Volumes

Problem Solving with Volumes (AQA GCSE Maths)

Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

Problem Solving with Volumes

How can I solve problems when its not a "standard" 3D shape?

  • Often the shape in a question will not be a standard cuboid, cone, sphere, etc

  • It will likely either be:

    • A prism (3D shape with the same cross-section running through it)

    • A portion or fraction of a standard shape (a hemisphere for example)

  • If the shape is a prism, recall that the volume of a prism is the cross sectional area × its length

    • The cross-sectional area may be a compound shape, such an an L-shape, or a combination of a rectangle and a triangle for example

  • If the shape is a fraction of a standard shape, consider the "full" version of the shape and then find the appropriate fraction of it

    • A hemisphere is half a sphere

    • A frustum is a truncated (chopped-off) cone or pyramid

      • The volume of a frustum will be the volume of the smaller cone or pyramid subtracted from the volume of the larger cone or pyramid

Examiner Tips and Tricks

  • Before you start calculating, make a quick note of your plan to tackle the question

    • e.g. "find the area of the triangle and the rectangle, add together, times by the length"

Worked Example

A doll's house is in the shape of a prism pictured below. The prism consists of a cuboid with a triangular prism on top of it. The cross section of the triangular prism is an isosceles right-angled triangle. Find the volume of the doll's house.

3-7-1-problem-solving-with-volume-1

Our strategy is to find the area of the triangle and the rectangle and add them together to find the cross-sectional area, and then multiply this by the length to find the volume

As it is an isosceles triangle, length a equals 20 space cm

We can then use Pythagoras to find length b

b equals square root of 20 squared plus 20 squared end root equals square root of 800 equals 20 square root of 2

Length c will also be 20 square root of 2

Finding the area of the triangle using Area equals 1 half cross times base cross times height

Triangle space Area space equals 1 half cross times 20 cross times 20 equals 200 space cm squared

Finding the area of the rectangle

40 cross times 20 square root of 2 equals 800 square root of 2 space cm squared

The total cross-sectional area is therefore the triangle plus the rectangle

200 space plus space 800 square root of 2 space cm squared space equals space 1 space 331.37085... space cm squared

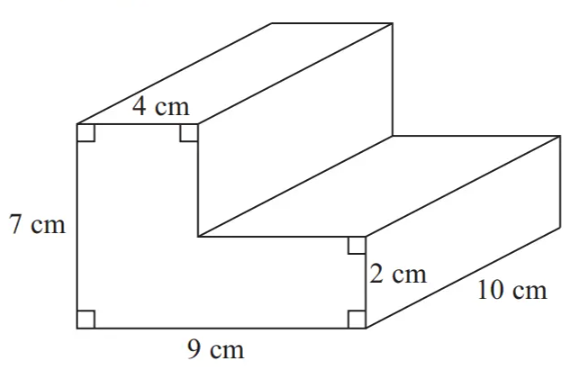
Finding the volume of the prism by multiplying the cross-sectional area by the length

open parentheses 200 plus 800 square root of 2 close parentheses cross times 60 equals 12000 plus 48000 square root of 2 space cm cubed equals 79 space 882.25099... space cm cubed

Rounding to 3 significant figures

79 900 cm3

Worked Example

The diagram shows a truncated cone (a frustum). Using the given dimensions, find the volume of the frustum.

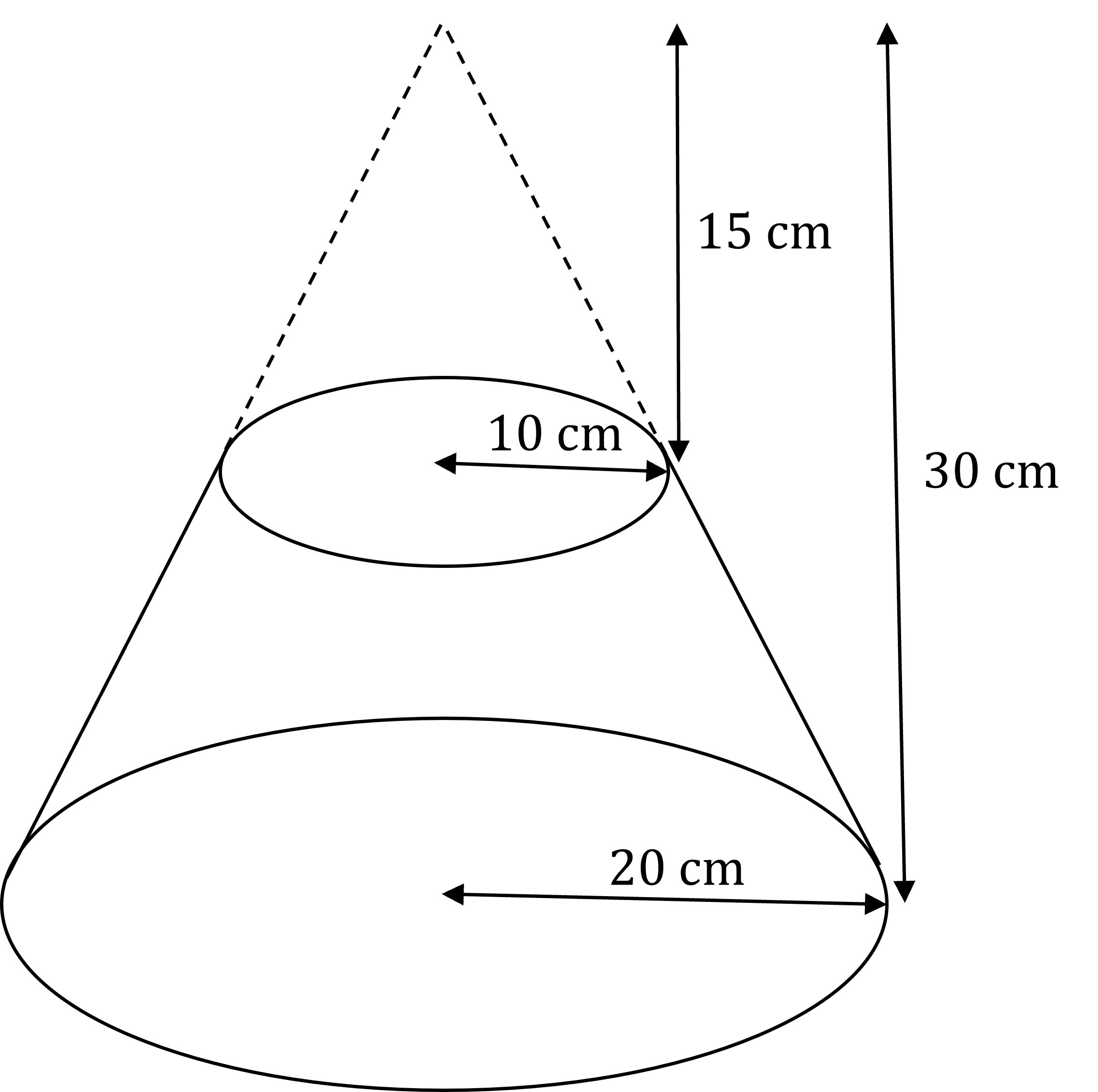
3-7-1-problem-solving-with-volume-2

To find the volume of the frustum, find the volume of the larger cone (30 cm tall, with a radius of 20 cm), and subtract the volume of the smaller cone (15 cm tall, with a radius of 10 cm)

Formula for the volume of a cone: 1 third pi space r squared straight h

Calculate the volume of the larger cone

V subscript L equals 1 third cross times straight pi cross times 20 squared cross times 30 equals 4000 straight pi equals 12 space 566.37061... space cm cubed

Calculate the volume of the smaller cone

straight V subscript straight S equals 1 third cross times straight pi cross times 10 squared cross times 15 equals 500 straight pi equals 1 space 570.796327... space cm cubed

Find the difference

V subscript L minus V subscript S equals 4000 straight pi minus 500 straight pi equals 3500 straight pi equals 10 space 995.57429... space cm cubed

Round to 3 significant figures 

11 000 cm3 

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:VolumeNext:Surface Area
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.