Revision NotesPast Papers
GCSEMathsAQAFoundationRevision NotesGeometry & MeasuresPythagoras & TrigonometryAngles of Elevation & Depression

Angles of Elevation & Depression (AQA GCSE Maths): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

AQA Maths: FoundationOCR Maths: HigherAQA Maths: HigherEdexcel Maths: FoundationEdexcel Maths: Higher

Elevation & Depression

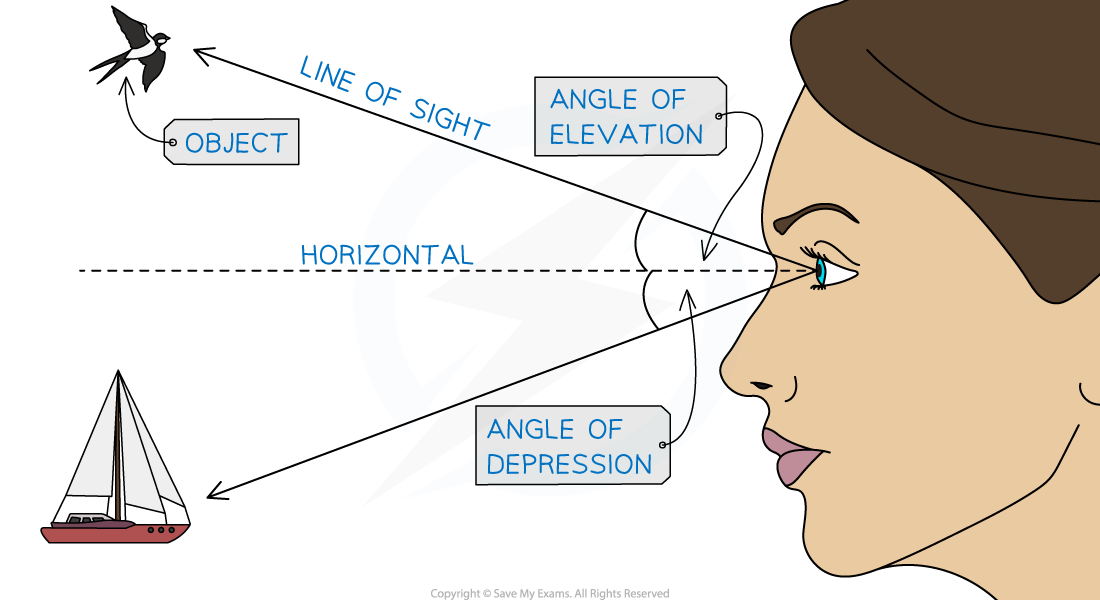
What are angles of elevation and depression?

  • An angle of elevation or depression is the angle measured between the horizontal and the line of sight

    • Looking up at an object creates an angle of elevation

    • Looking down at an object creates an angle of depression

  • Right-angled trigonometry can be used to find

    • an angle of elevation or depression

    • or a missing distance

  • The tan ratio is often used in real-life scenarios

    • You may know the height of an object and want to find the distance you are from it

    • You may know the distance you are from an object and want to find its height

Diagram showing a person's face with a horizontal reference line at eye level. A diagonal line of sight pointing up towards a bird forms an angle of elevation and a line of sight pointing down towards a boat forms an angle of depression.

Examiner Tips and Tricks

It may be useful to draw more than one diagram if the triangles that you are interested in overlap one another.

Worked Example

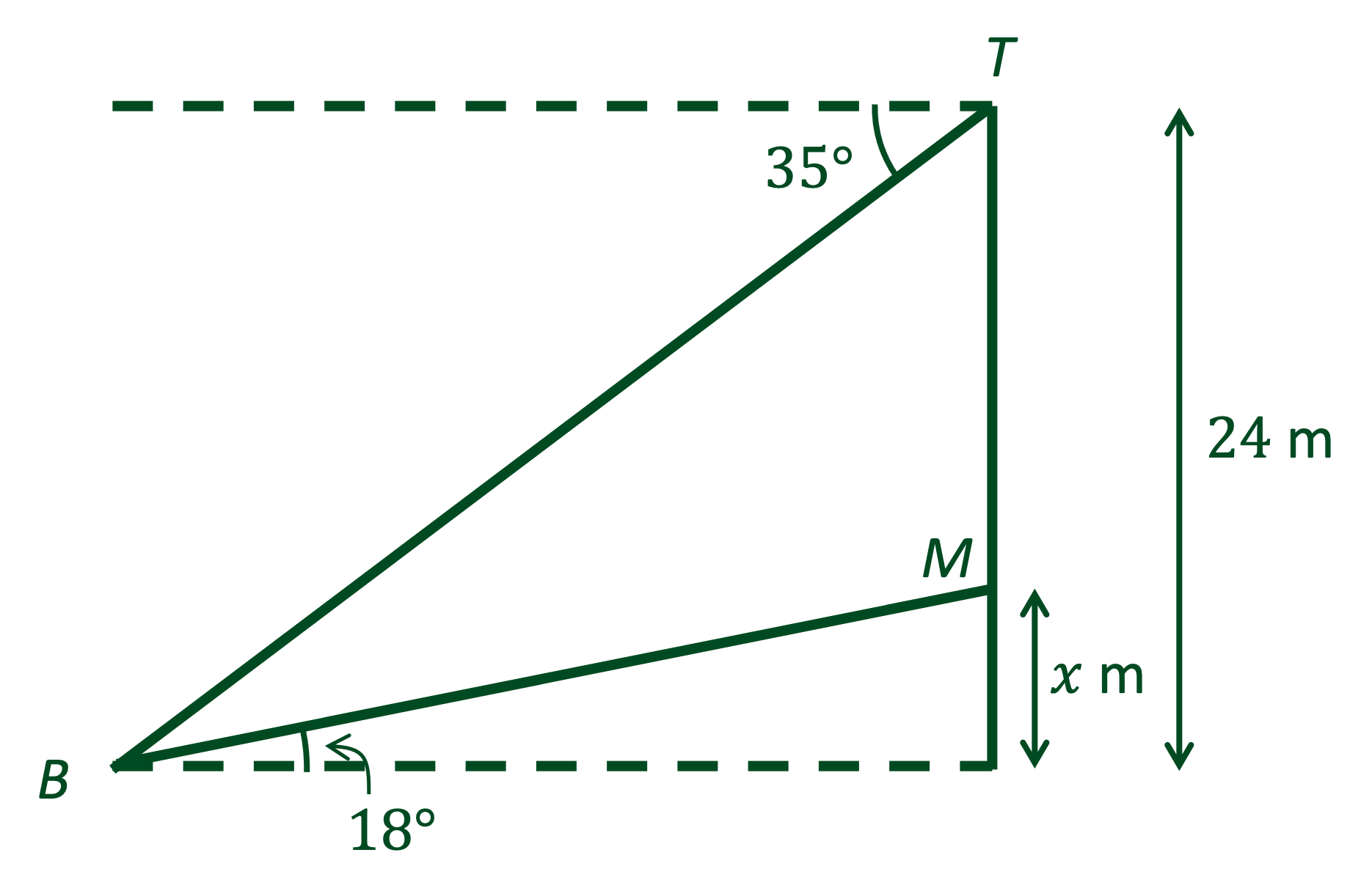
A cliff is perpendicular to the sea and the top of the cliff, T, stands 24 metres above the level of the sea.

The angle of depression from the top of the cliff to a boat at sea is 35°.

At a point xmetres vertically up from the foot the cliff is a flag marker, M.

The angle of elevation from the boat, B, to the flag marker is 18°.

(a) Draw a diagram of the situation. Label all the angles and distances given above.

Diagram showing a triangle BFT with an angle of elevation 35º marked between BT and the horizontal. The length Ft is equal to 24 m. A line is drawn from B to a point M on the line FT, such that angle FBM is equal to 18º. The height of MF is x m.

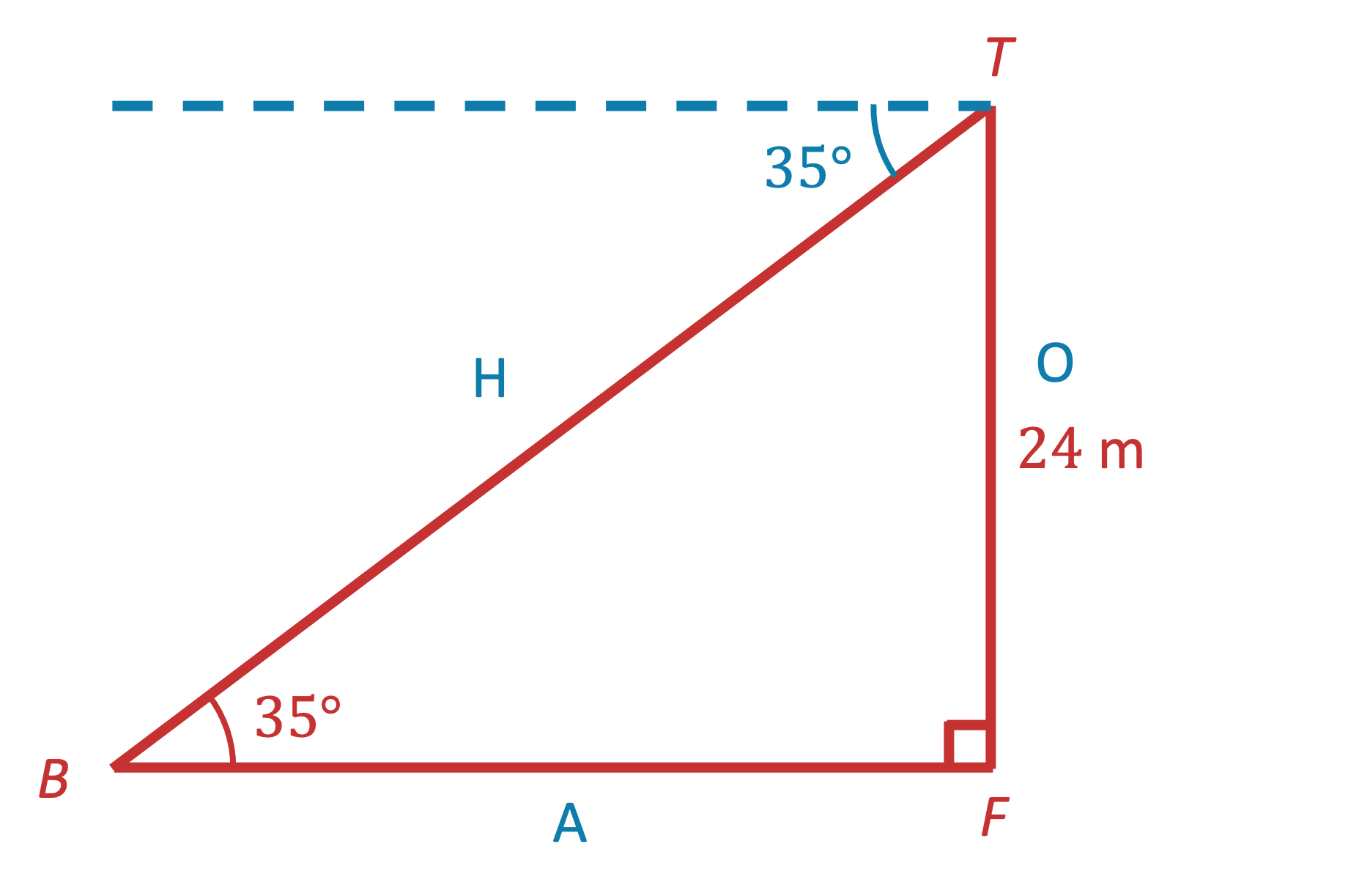
(b) Find the distance from the boat to the foot of the cliff.

Consider triangle TBF where F is the foot of the cliff
Angle TBF = 35º because of alternate angles

Use SOHCAHTOA to find the missing distance
We know the opposite (TF) and we want to find the adjacent (BF), so use tan space theta equals straight O over straight A

Triangle TBF with angle TBF = 35º, TF = 24 m. BT is marked as the hypotenuse, TF as the opposite and BF as the adjacent.

table row cell tan space 35 end cell equals cell fraction numerator 24 over denominator B F end fraction end cell row cell B F end cell equals cell fraction numerator 24 over denominator tan space 35 end fraction end cell row cell B F end cell equals cell 34.27555... end cell end table

BF = 34.3 m (3 s.f.)

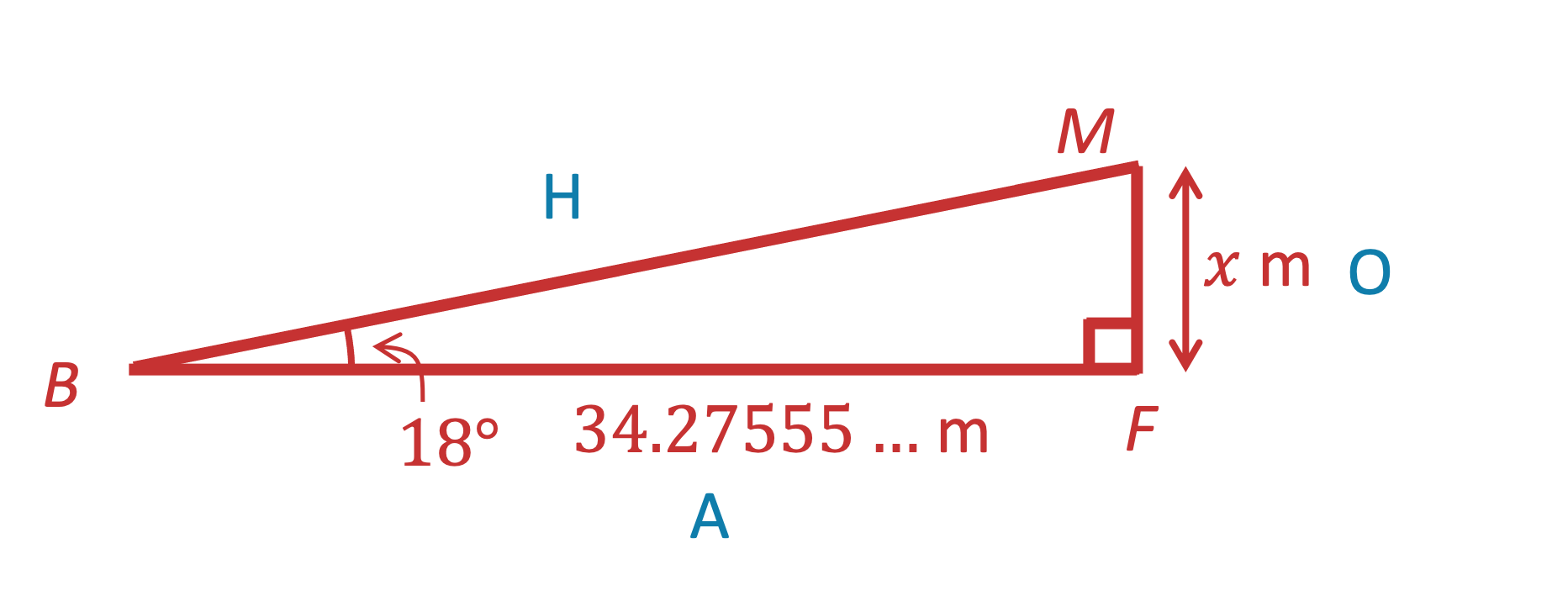
(c) Find the value of x.

Consider triangle MBF

Use SOHCAHTOA to find the missing distance
We know the adjacent (BF) and we want to find opposite (MF), so use tan space theta equals O over A

Triangle MBR with angle MPF = 18º, BF = 34.27555... m and MF = x m.

table row cell tan space 18 end cell equals cell fraction numerator x over denominator 34.27555... end fraction end cell row cell 34.27555... space tan space 18 end cell equals x row x equals cell 11.1368... end cell end table

bold italic x bold equals bold 11 bold. bold 1 m (3 s.f.)

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Trigonometry to Find AnglesNext:Exact Trig Values
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.