GCSEGeographyOCRGeography BRevision NotesGeographical SkillsGeographical SkillsNumerical & Statistical Skills

Numerical & Statistical Skills (OCR GCSE Geography B)

Revision Note

Test yourself
Jacque Cartwright

Written by: Jacque Cartwright

Reviewed by: Bridgette Barrett

Numerical Skills

  • A range of numerical skills are needed throughout the final exam papers

Proportion and ratio

  • Proportion is relating one part to the whole

    • In a group of 100 if there are 20 people who are 15 and 80 people who are 14

    • The proportion of those 15-year-olds is 20/100 or 20%

  • Ratio is the comparison of two quantities 

    • In a group of 100 if there are 20 people who are 15 and 80 people who are 14

    • The ratio is 1:4 so for every person that is 15 there are 4 people who are 14

Magnitude

  • Refers to the relative size usually of an event such as an earthquake

Frequency

  • Refers to how often something occurs

Worked Example

Analyse Figure 1

For 1960 calculate the ratio of rural population to urban population

(1 Mark)

Answer 

  • Any of the following could be awarded 1 mark

    • 5.5:1

    • 550 to 100

    • 55:10

    • 110:20 (or 110 to 20)

    • 22:4 (or 22 to 4)

    • 11:2 (or 11 to 2)

Examiner Tips and Tricks

Always check when making calculations what the question has asked you to do. Is it asking for units to be stated or calculate to the nearest whole number or quote to 2 decimal places? 

Statistics

Percentage and percentage change

  • To give the amount A as a percentage of sample B, divide A by B and multiply by 100

    • In 2020, 25 out of 360 homes in Catland were burgles. What is the percentage (to the nearest whole number) of homes burgled?

    • 25 divided by 360 cross times 100 space equals 6.94 space open square brackets space t o space n e a r e s t space w h o l e space n u m b e r close square brackets space equals 7 percent sign

  • A percentage change shows by how much something has either increased or decreased

  • P e r c e n t a g e space c h a n g e space equals fraction numerator f i n a l space v a l u e space minus o r i g i n a l space v a l u e over denominator o r i g i n a l space v a l u e end fraction cross times 100

    • In 2021 only 21 houses were burgled. What is the percentage change in Catland?

    • fraction numerator 21 minus 25 over denominator 25 end fraction cross times 100 equals negative 16 percent sign

    • There has been a decrease of 16% in the rate of burglaries in the Catland area

  • Do remember that a positive figure shows an increase but a negative is a decrease

Worked Example

Study Figure 1 which shows sources of greenhouse gas emissions in the European Union for 1990 and 2018

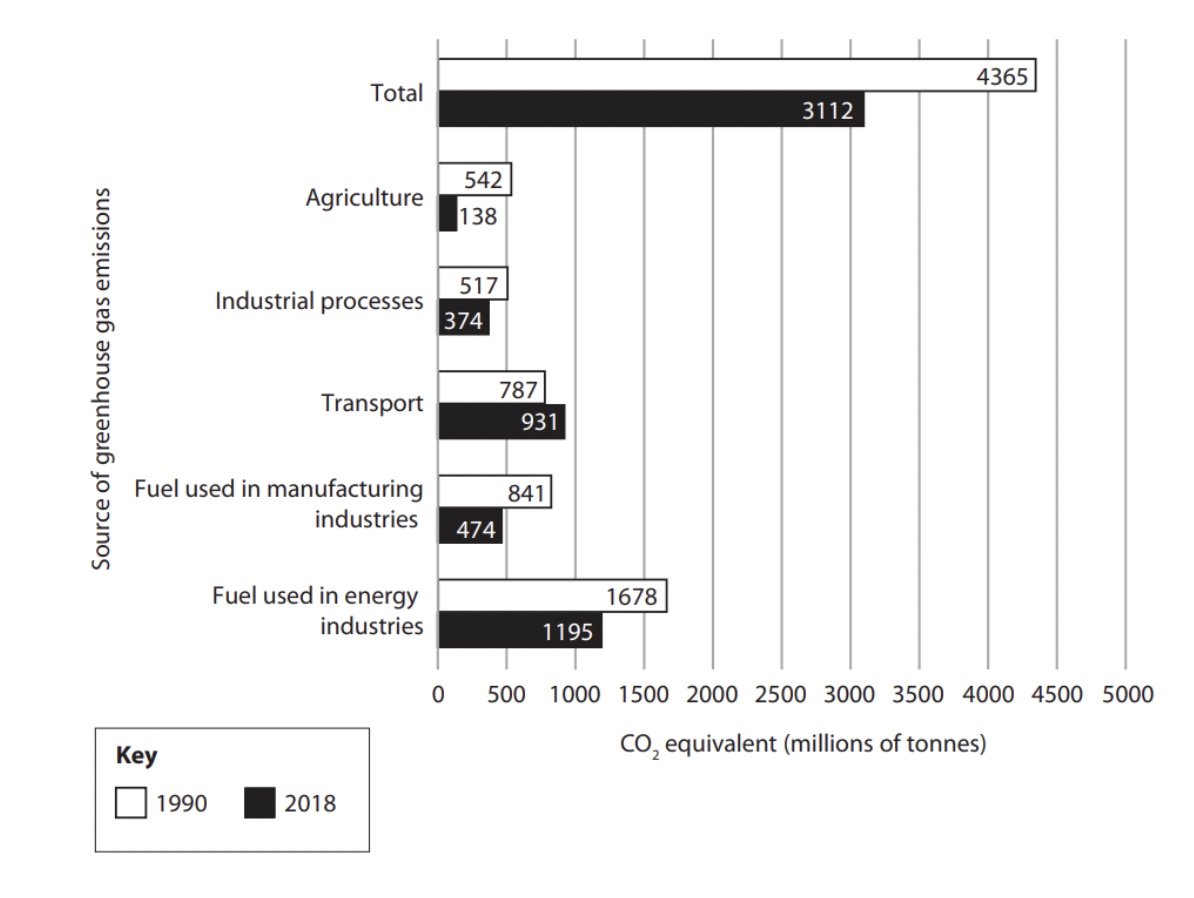
f3609348-eed6-41d5-b102-123dcef8c4eb

Calculate the percentage decrease in total emissions (CO2 equivalent) between 1990 and 2018

Give your answer to one decimal place 

Show your working

(2 marks) 

  • One mark is awarded for the working out

  • One mark is awarded for the answer to one decimal place

Answer

  • Emissions in 1990 = 3112

  • Emissions in 2018 = 4365

  • 3112/4365 = 0.7129 x 100 = 71.29 

  • 100 - 71.29 = 28.71 [1]

  • To one decimal place = 28.7% [1]

Statistics:

  • This is the study and handling of data, which includes ways of gathering, reviewing, analysing, and drawing conclusions from data

Measures of central tendency

  • Mean = average value (all the values added and divided by the number of items)

  • Median = middle value when ordered in size

  • Mode = most common value

  • Range = difference between the highest value and lowest value

Sample site

1

2

3

4

5

6

7

Number of pebbles

184

90

159

142

64

64

95

  • Taking the example above to calculate:

  • Mean - fraction numerator 184 plus 90 plus 159 plus 142 plus 64 plus 64 plus 95 over denominator 7 end fraction equals 798 over 7 equals 114

  • Median - reordering by size = 64 space 64 space 90 space begin bold style stretchy left square bracket 95 stretchy right square bracket end style space 142 space 159 space 184 = 95 is the middle value

  • Mode - only 64 appears more than once

  • Range - 184 space minus space 64 space equals space 120

Upper and lower quartiles

  • These are the values of a quarter (25%) and three-quarters (75%) of the ordered data

Number of shoppers

2

3

6

6

7

9

13

14

17

22

22

 

 

 

Lower quartile

 

 

Median

 

 

Upper quartile

 

 

  • The interquartile range is the difference between the upper and lower quartile

  •  17 space minus space 6 space equals space 11

Worked Example

Study Figure 1 which shows the Human Development Index (HDI) levels for states and federal territories in Malaysia 

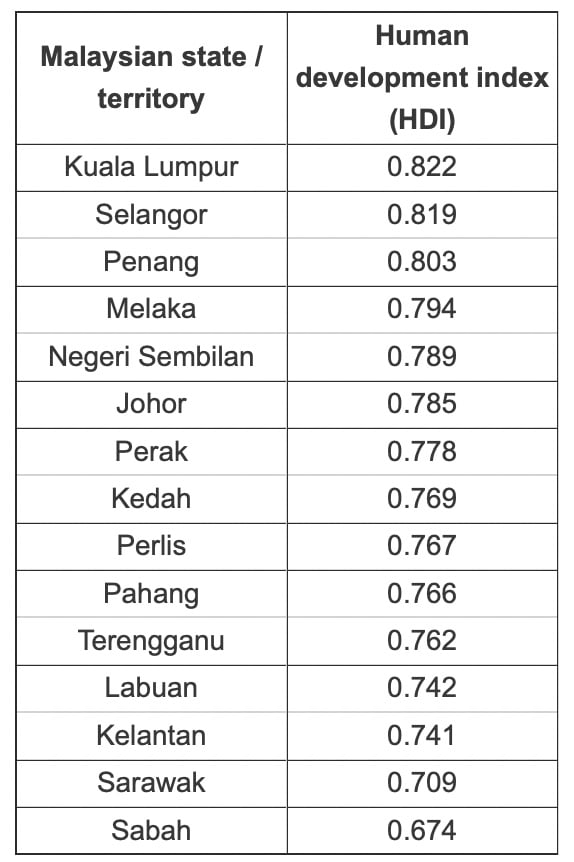
d386b050-3adf-43f3-abe3-ac5494b294cc

Calculate the interquartile range of HDI scores given in Figure 1.

Show your working

(2 marks)

Answer 

  • Lower quartile (Labuan 0.742) and upper quartile (Melaka 0.794) [1]

  • Subtract the lower quartile from the upper quartile.
    0.794 – 0.742 (1) and 1 mark for the correct answer of 0.052 [1]

Bivariate data

  • Data that consists of 2 variables is called bivariate data

  • Data can be either quantitative or qualitative or both 

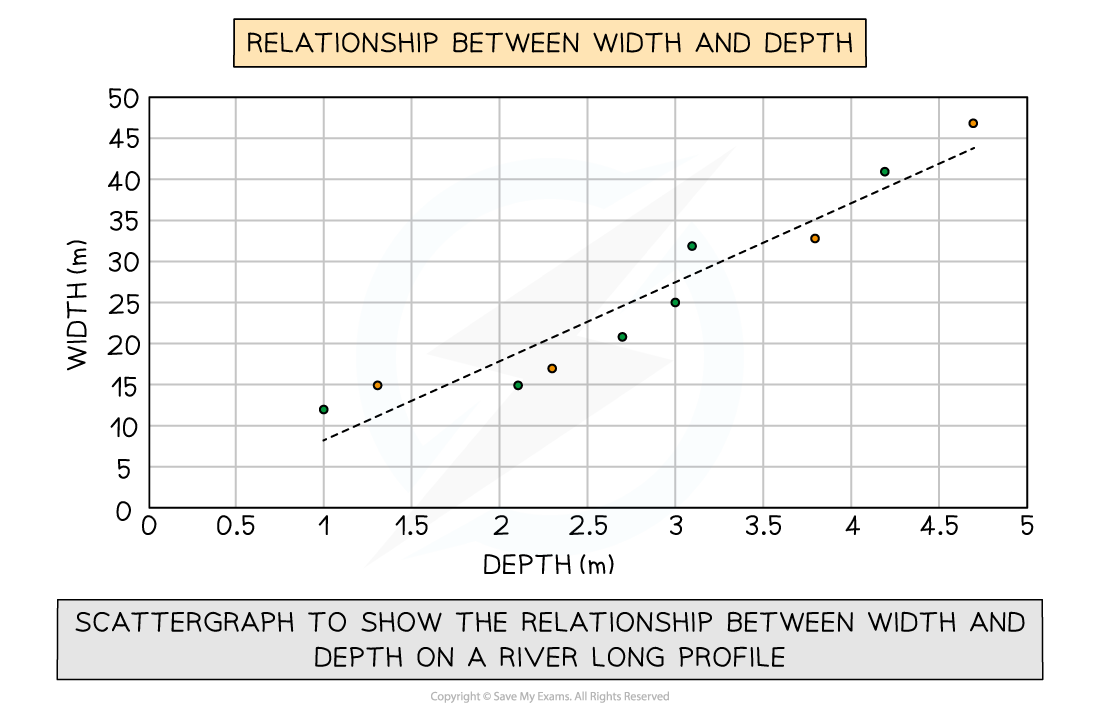
    • In a river study, bivariate data would be used to show the relationship (correlation) between different river characteristics such as the relationship between the width and depth of the river channel

  • The two variables can depend on each other, with one variable influencing the other

  • The bivariate data would then have an independent variable and a dependent variable

    • For example, rainfall is an independent variable and runoff is a dependent variable

    • This is because the amount of run-off is dependent on the amount of rainfall, but rainfall is not influenced by run-off

  • The relationship between dependent and independent variable can be seen as a positive or negative correlation or relationship

    • A positive correlation means that if the independent variable increases then the dependent would also increase

      • The more it rains, the higher the rate of run-off

    • A negative correlation is when the independent variable increases but the dependent variable decreases

      • Rainfall increased, but the rate of run-off did not

  • The relationship (correlation) between two variables (bivariate) is often shown using a scattergraph

Scatter graph

  • Scattergraphs are used to show the relationship between two variables

    • Points should not be connected

    • A 'line of best fit' or 'trendline' can be added to show the correlation

      • This is a line or curve that shows the general pattern or direction of the data over time

  • Interpolation is where the line of best fit is used for a value that is within the plotted points

  • Extrapolation is where the line of best fit is extended beyond the plotted points to gain a future value

Scattergraphs - strengths and weaknesses

Strengths

Limitations

Clearly shows data correlation

Data points cannot be labelled

Shows the spread of data

Too many data points can make it difficult to read

Makes it easy to identify anomalies and outliers

Can only show the relationship between two sets of data

Scattergraph showing the relationship between width and depth on a river's long profile

Scattergraph showing correlation between width and depth on a river profile. Points with trend line indicate width increases with depth up to 50 meters.
Scatter graph to show the relationship between width and depth on a river's long profile

Types of correlation

  • Positive correlation

    • As one variable increases, so too does the other

    • The line of best fit goes from the bottom left to the top right of the graph

  • Negative correlation 

    • As one variable increases the other decreases

    • The line of best fit goes from the top left to the bottom right of the graph

  • No correlation

    • Data points will have a scattered distribution

    • There is no relationship between the variables

Examiner Tips and Tricks

When extrapolating data, you must be cautious. It is unknown what could occur beyond the given data points - it could decline, flatten or increase. In the exam if asked about extrapolating information from scattergraphs or why a student's result wasn't accurate, it is best to reply by saying 'they were using a value outside of the plotted data points'.

Last updated:

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Graphs & DiagramsNext:Pictorial & Written Material
    Author
    Reviewer
    Jacque Cartwright

    Author: Jacque Cartwright

    Expertise: Geography Content Creator

    Jacque graduated from the Open University with a BSc in Environmental Science and Geography before doing her PGCE with the University of St David’s, Swansea. Teaching is her passion and has taught across a wide range of specifications – GCSE/IGCSE and IB but particularly loves teaching the A-level Geography. For the past 5 years Jacque has been teaching online for international schools, and she knows what is needed to get the top scores on those pesky geography exams.

    Bridgette Barrett

    Author: Bridgette Barrett

    Expertise: Geography Lead

    After graduating with a degree in Geography, Bridgette completed a PGCE over 25 years ago. She later gained an MA Learning, Technology and Education from the University of Nottingham focussing on online learning. At a time when the study of geography has never been more important, Bridgette is passionate about creating content which supports students in achieving their potential in geography and builds their confidence.