Here is a sketch of where
is a quadratic function.
The graph
intersects the
-axis at
and
has a maximum point at
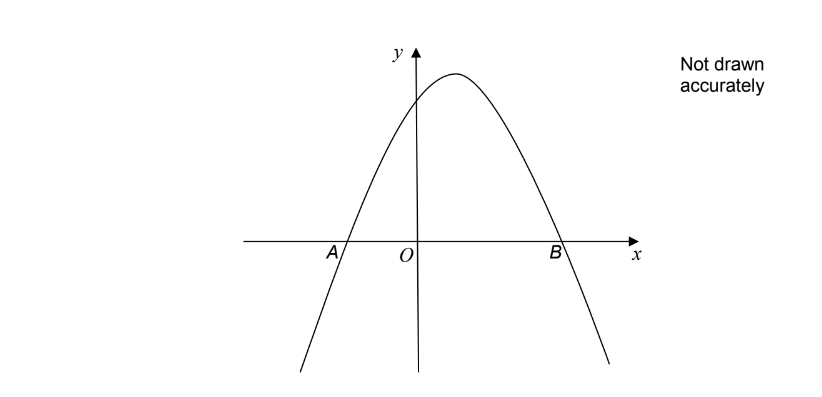
Work out the coordinates of .
The equation has exactly one solution.
Write down the value of .
Did this page help you?
Exam code: 8365
Here is a sketch of where
is a quadratic function.
The graph
intersects the -axis at
and
has a maximum point at

Work out the coordinates of .
How did you do?
The equation has exactly one solution.
Write down the value of .
How did you do?
Did this page help you?
Here is a sketch of where
is a point on the curve.

Work out the value of .
How did you do?
is a point on the curve with
-coordinate
Work out the -coordinate of
.
How did you do?
Did this page help you?
The function has domain
Here is the graph of

Write down the equation of the line of symmetry of the graph.
How did you do?
Use the graph to work out the solutions of
Give your answers to 1 decimal place.
How did you do?
Did this page help you?
Here is the graph of for values of
between 0 and 6

By drawing a suitable linear graph on the grid, work out approximate solutions to
How did you do?
Did this page help you?
The graph shown has the equation
It has a stationary point at
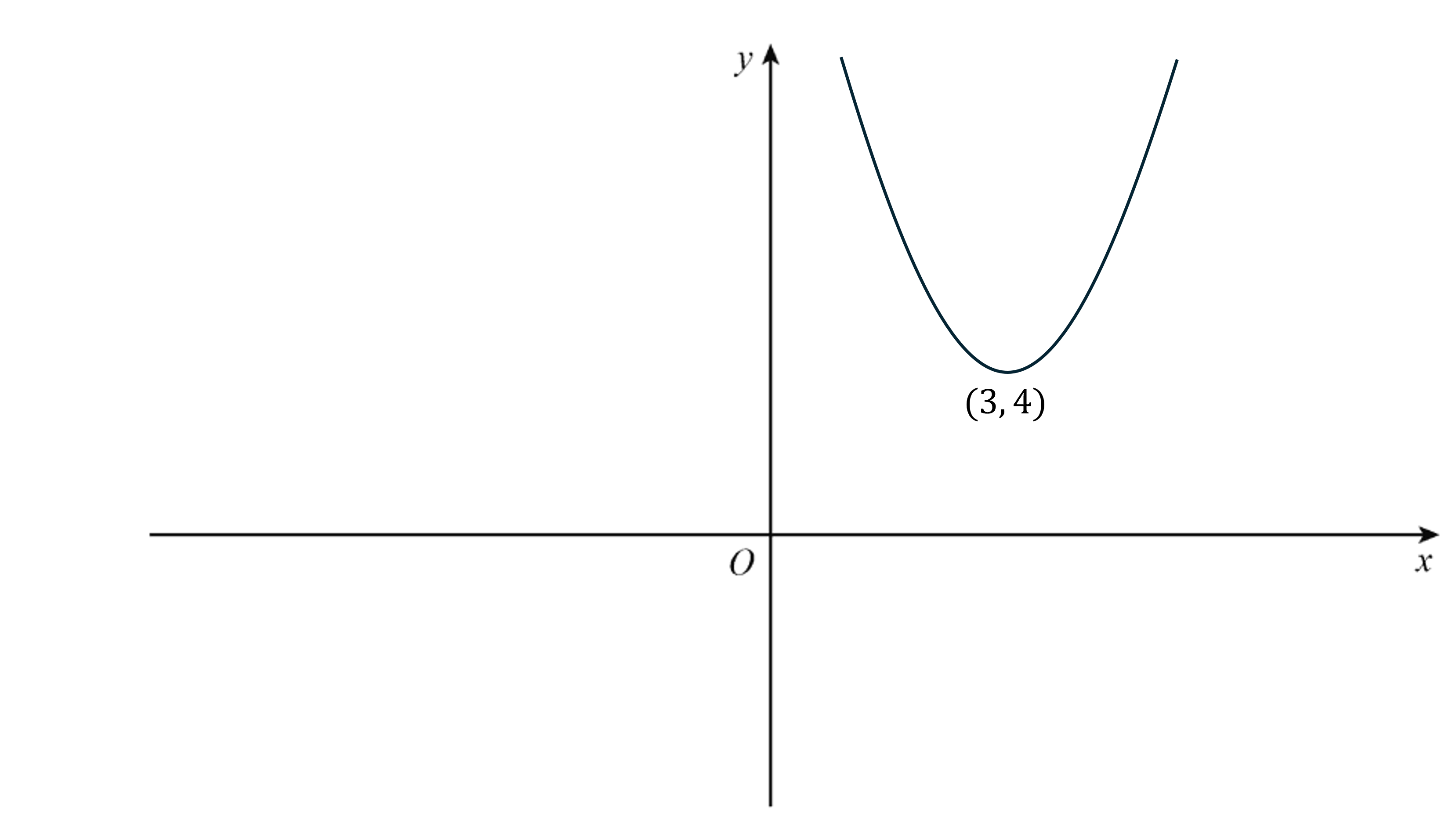
Work out the values of and
.
How did you do?
Did this page help you?
The curve
has a maximum point at
has a minimum point at
intersects the -axis at
.
The curve crosses the -axis at three distinct points.
On the axes below, sketch the curve.
Label the points and
on your sketch.

How did you do?
Did this page help you?
Here is a sketch of the curve where
and
are positive constants.
and
lie on the curve.

Work out the values of and
.
...............................
...............................
How did you do?
Did this page help you?
Here is a sketch of the curve
The curve intersects the -axis at
and
.

Complete the coordinates of and
.
How did you do?
Write down the range of values for for which
How did you do?
Did this page help you?
Here is the graph of for values of
from
to

By drawing a suitable linear graph on the grid, work out approximate solutions to
How did you do?
Did this page help you?
Here is a sketch of where
and
are constants.
The graph intersects the -axis at
and
and the
-axis at point

Work out the coordinates of point .
You must show your working.
How did you do?
Did this page help you?
The graph of is shown, where
.

The line intersects the graph exactly once.
Find the value of .
How did you do?
Did this page help you?
is a cubic curve with a maximum and a minimum stationary point.
The -coordinate of the minimum point is
.
The -coordinate of the maximum point is
.
is a point on the curve.
The tangent at has a negative gradient.
Sketch the curve on the grid below and show the coordinates of the stationary points.
How did you do?
Did this page help you?
The continuous curve g(
) has exactly two stationary points.
The stationary points are
a maximum point at where
and
a minimum point at
On the axes below, sketch the curve.
Label points and
on your sketch.

How did you do?
Did this page help you?
The graph of is shown, where
and
are positive constants.

The graph has a -intercept of
and passes through the point
By finding the values of and
, work out the equation of the graph.
Give your answer in the form where
and
are integers and where
is the smallest positive integer possible.
How did you do?
Did this page help you?