Sine, Cosine Rule & Area of Triangles (AQA GCSE Further Maths)

Revision Note

Test yourself

Written by: Paul

Reviewed by: Dan Finlay

Pythagoras' theorem and SOHCAHTOA only work in right-angled triangles
The Sine Rule and Cosine Rule allow us to answer triangle questions for ANY triangle
The Area of a Triangle Formula is an alternative to $\frac{1}{2} b h$

Did this video help you?

Sine & Cosine Rules

What are the sine rule and cosine rule formulae?

Before applying these formulas it is useful to label the triangle using a system of 'opposites'

General Triangle labelled, IGCSE & GCSE Maths revision notes

Note how lowercase letters are used for side lengths and capital letters for angles
- make sure an angle and the side opposite it have the same letter
Sine Rule

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

sin 90° = 1 so if one of the angles is 90°, this becomes ‘SOH’ from SOHCAHTOA
The sine rule can also be 'flipped over'

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

This is more useful when we are using the rule to find angles
Cosine Rule

$a^{2} = b^{2} + c^{2} - 2 b c \cos A$

cos 90° = 0 so if A = 90°, this becomes Pythagoras’ Theorem
The cosine rule is 'cyclic' so there are two other versions of it

$b^{2} = a^{2} + c^{2} - 2 a c \cos B c^{2} = a^{2} + b^{2} - 2 a b \cos C$

but once you are used to using cosine rule, there's only really one version
- you just need to 'cycle' a, b and c around accordingly for a specific question
Note that it's always the angle between the two sides in the final term
Questions can become algebraic when side lengths are replaced by letters and expressions
- Use the same rules but put brackets around expressions like (x + 3)

What is the ambiguous case of the sine rule?

In some circumstances, it is possible to get two possible answers using sine rule
- this arises when the angle you are trying to find could be either acute or obtuse
Consider the triangle below

Sine-Rule-Ambiguous-case, IGCSE & GCSE Maths revision notes

You know the pair a and A and half of the pair c and C (c = 34)
- However there are two possible locations for the third vertex of the triangle (labelled C₁ and C₂)
- So there are two possible angles for C (x and y on the diagram)
(Most) calculators will only give one answer when using inverse sine ( $\sin^{- 1}$ )
- this will be the acute angle
- if the obtuse angle is required, subtract the acute angle from 180°
Questions will state, or imply, whether the acute or obtuse angle is required
- or could ask you to find both possibilities!
There is no 'ambiguous' case for the cosine rule

How do I know whether to use sine rule or cosine rule?

Sine rule is used when you know a 'pair' and half of the pair involving the unknown we are asked to find
- e.g. a question may give us side a and angles A and B, then ask us to find side b
  (you know the pair a and A, and half of the pair b and B)
Cosine rule is used in two circumstances
- when questions gives us an angle and the two sides that make it
  - this allows us to find the side opposite the given angle
  - e.g. a question may give us sides b, c and angle A
    (this would allow us to find the side a)
- when questions give us all three sides of a triangle and we are required to find an angle
  - in this case the rearranged version of cosine rule may be helpful

$\cos A = \frac{b^{2} + c^{2} - 2 b c \cos A}{2 b c}$

then use inverse cos ( $\cos^{- 1}$ ) to find A
you may prefer to substitute known values into the 'regular' version of cosine rule and then rearrange

Examiner Tips and Tricks

In trickier exam questions, you may have to use both the cosine rule and the sine rule
For the sine rule, if you are finding a side, use the version of the formula that has the sides on the numerators; if you are finding an angle, put the sines on the numerators
If your calculator gives you a ‘Maths ERROR’ message when trying to find an angle using the cosine rule, you probably subtracted things the wrong way around when you rearranged the formula

Worked Example

The diagram below shows a sketch of a triangle, where angle ACB is obtuse.

General-Triangle-with-values-2, IGCSE & GCSE Maths revision notes

a) $\begin{matrix} \end{matrix}$ Show that the cosine of angle ABC is exactly $\frac{487}{592}$ .

You know all three lengths and want to show a result involving cosine - so use cosine rule!
Substitute values into cosine rule

$4 . 4^{2} = 4 . 8^{2} + 7 . 4^{2} - 2 \times 4.8 \times 7.4 \times \cos A B C$

Evaluate where possible, ensuring not to round as an exact answer is required later

$19.36 = 77.8 - 71.04 \cos A B C$

Rearrange to find an expression for $\cos A B C$

$\begin{array}{rcl} 71.04 \cos A B C & = & 77.8 - 19.36 \\ \cos A B C & = & \frac{58.44}{71.04} \end{array}$

Use your calculator to write/check this fraction is the same as the required answer

$∴ \begin{array}{rcl} \cos \end{array} \begin{array}{rcl} A \end{array} \begin{array}{rcl} B C \end{array} \begin{array}{rcl} = \end{array} \begin{array}{rcl} \frac{487}{592} \end{array}$

b) A student uses the sine rule and the answer to part (a) to calculate angle ACB.
Their final answer, rounded to one decimal place is 73.0°.
Explain why the student's final answer cannot be correct and find the correct size for angle ACB.

Angle ACB is obtuse so $90 ° < A C B < 180 °$

The answer 73.0° comes from using $\sin^{- 1} (. . .)$ and a calculator will always give an acute angle
The question says angle ACB is obtuse
To find the correct angle we need to subtract 73.0° from 180°

180° - 73.0° = 107.0°

Angle ACB = 107.0° (1 d.p.)

This is commonly known as the ambiguous case of the sine rule

Area of a Triangle

What is the area of a triangle formula?

The Area of a Triangle formula applies to any triangle set up using the system of 'opposites'

$Area = \frac{1}{2} a b \sin C$

As with cosine rule, there are 'cyclic' alternatives to this
- but rather than rememeber three formulae, remember one and change a, b and c accordingly
- e.g. $\frac{1}{2} b c \sin A$
sin 90° =1 so if C = 90°, this becomes $Area = \frac{1}{2} b h$
In genreal $\frac{1}{2} a b \sin C$ allows us to find the area without having to know or find the height
- it is particularly useful in non-right angled triangles
The questions encountered can be more algebra-based when side lengths are given as letters or expressions
- use brackets around expressions like (x + 3)
- check for any exact trigonometric values, like $\sin 30 = \frac{1}{2}$

Examiner Tips and Tricks

Try not to get bogged down in remembering different versions of the area of a triangle formula
- Spot that to use $\frac{1}{2} a b \sin C$ you need an angle and the two sides that form it

Worked Example

The diagram below shows triangle PQR where side PQ is 2x and angle P is 30°.
Given that the ratio of the sides PQ to PR is 2 : 3, find an expression for the area of the triangle in terms of x.

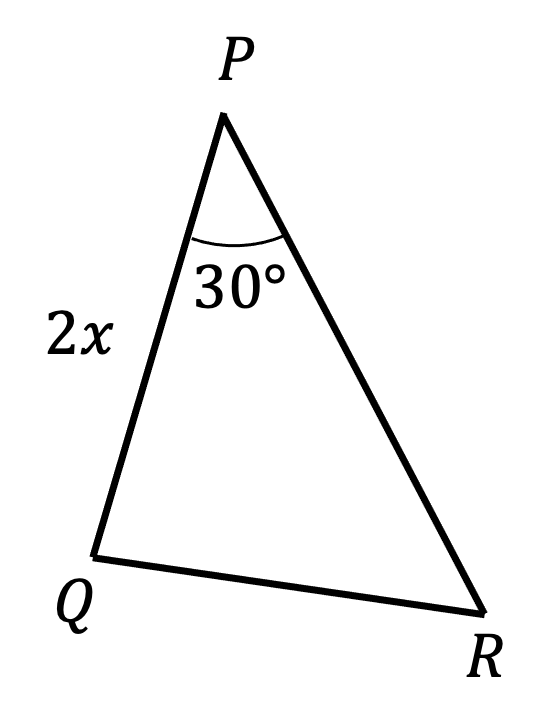
To use the area of a triangle formula we need two sides and the angle between them
So you need to find, in terms of x, the side PR using the given ratio

$\begin{array}{rcl} P : R \\ 2 : 3 \\ 2 x : 3 x \end{array}$

$∴ P R = 3 x$

Now apply the area of a triangle formula

$Area = \frac{1}{2} (2 x) (3 x) \sin 30 °$

Simplifying the right-hand side including evaluating $\sin 30 °$

$Area = \frac{1}{2} (6 x^{2}) (\frac{1}{2})$

$∴ Area = \frac{3}{2} x^{2}$ (square units)

Applications of Trigonometry

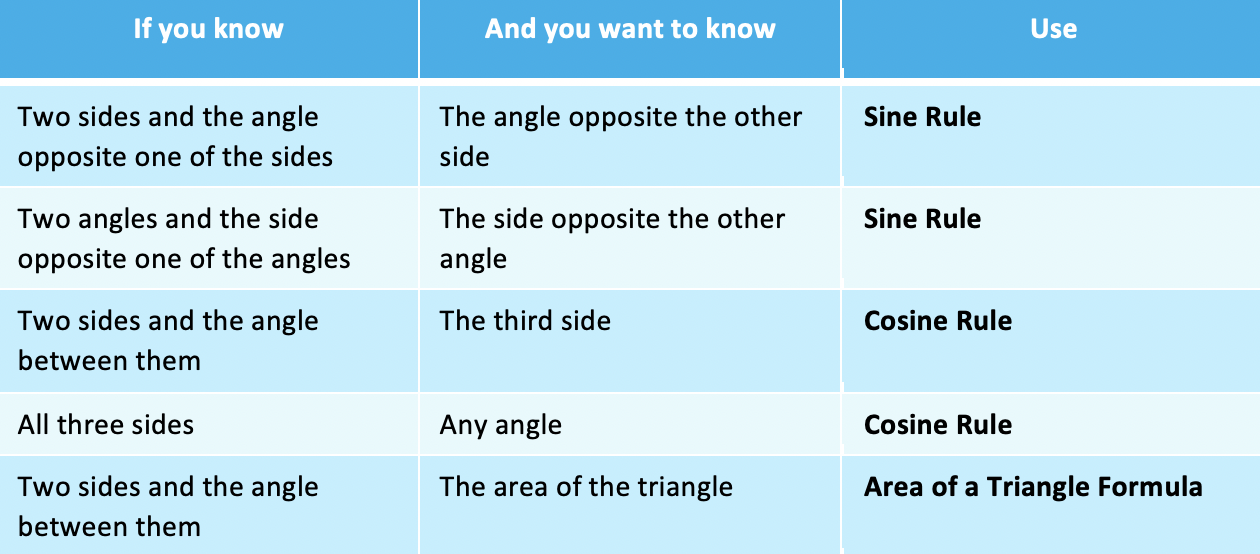
How do I choose which rule or formula to use

It is important to be able to decide which Rule or Formula to use to answer a question
This table summarises the possibilities:

Sine & Cosine Rules, Area of Triangle – Harder table, IGCSE & GCSE Maths revision notes

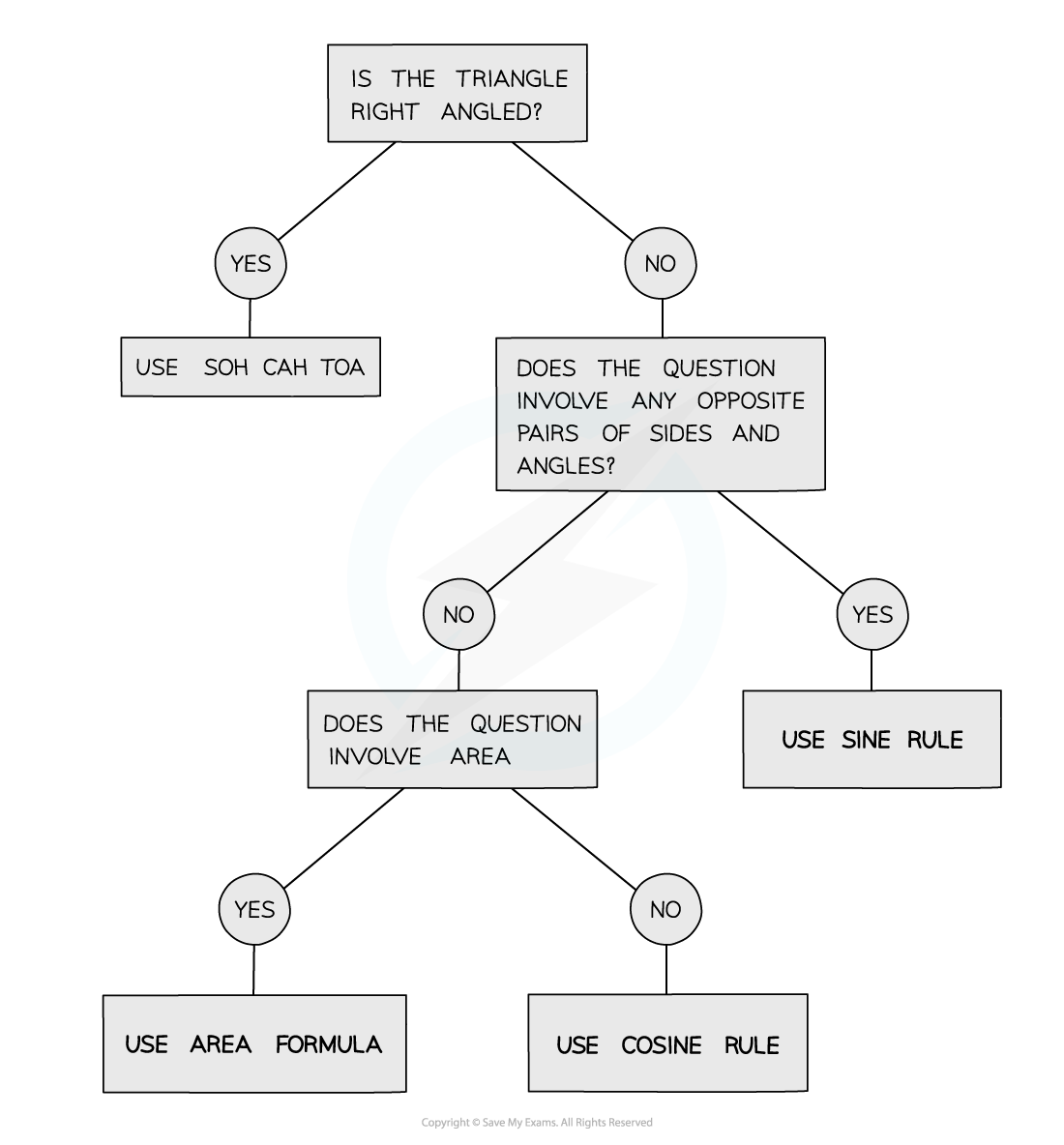
What problems will I be asked to solve using trigonometry?

Problems in trigonometry may involve any, or more than one
- Pythagoras' theorem
- SOHCAHTOA
- Sine rule
- Cosine rule
- Area of a triangle
Beyond 2D triangles you may be asked to solve problems involving
- more complicated 2D shapes that have parts or sections that can be considered as a triangle
  - e.g. a trapezium
- 3D shapes that have triangular parts or features
  - e.g. a triangular prism, the cross section of a cone
Many problems will involve algebraic answers
- sides may be given in terms of a variable such as x
- you may be asked to find an expression for a length or area "in terms of x"
Problems may involve surds, arising from exact values to common trigonometric ratios
- e.g. $\sin 60 ° = \frac{\sqrt{3}}{2}, \cos 45 ° = \frac{1}{\sqrt{2}} (= \frac{\sqrt{2}}{2})$
- You need to learn these exact values

Worked Example

The diagram below shows a cone with slant height of $2 x$ cm.
Given that angle ABC is 30°, show that the diameter of the base, $d$ cm, is given by the expression $d^{2} = 4 x^{2} (2 - \sqrt{3})$ .

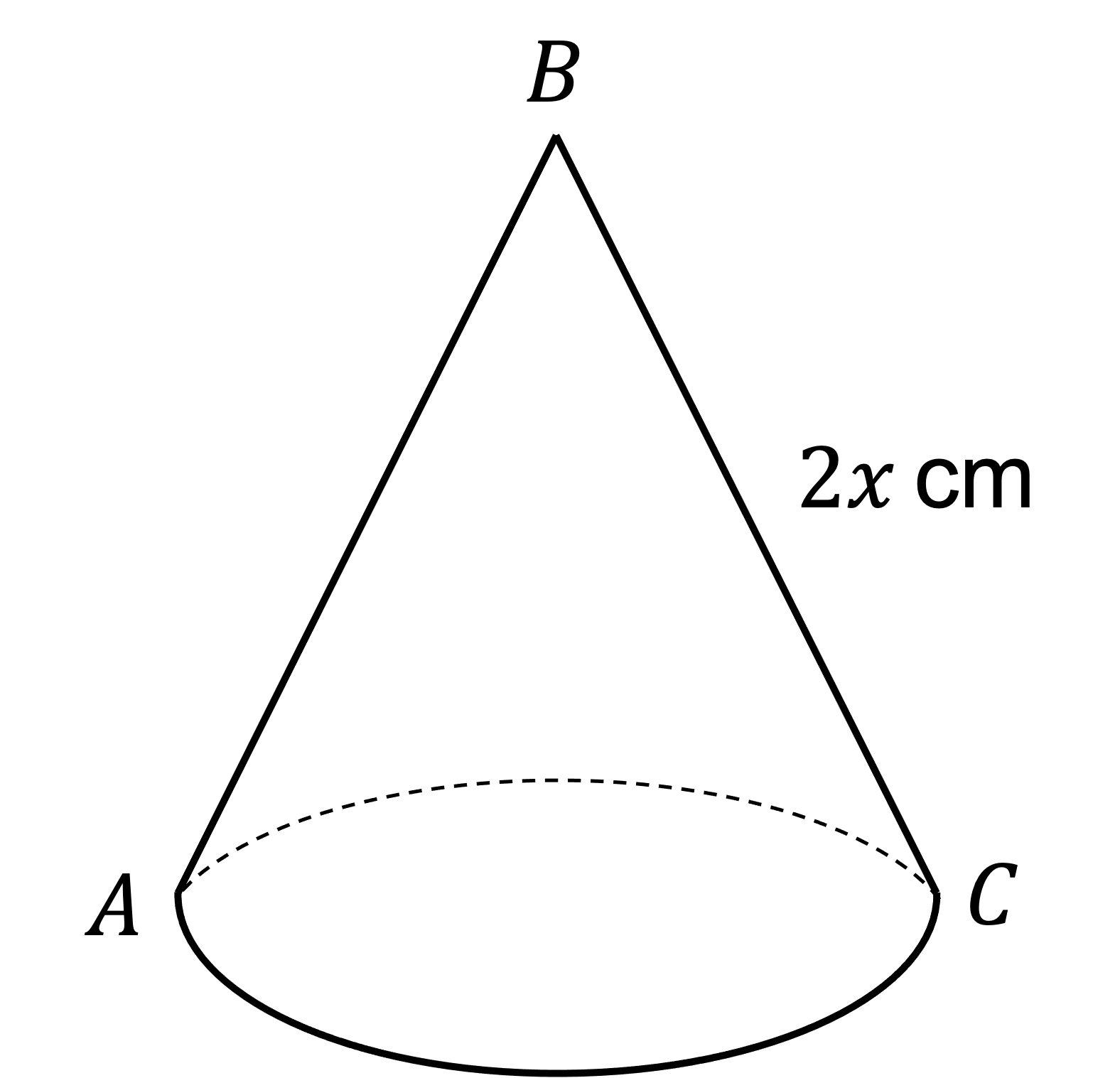
BA = BC by symmetry
Draw a cross section through the centre of the cone and include any angles and lengths

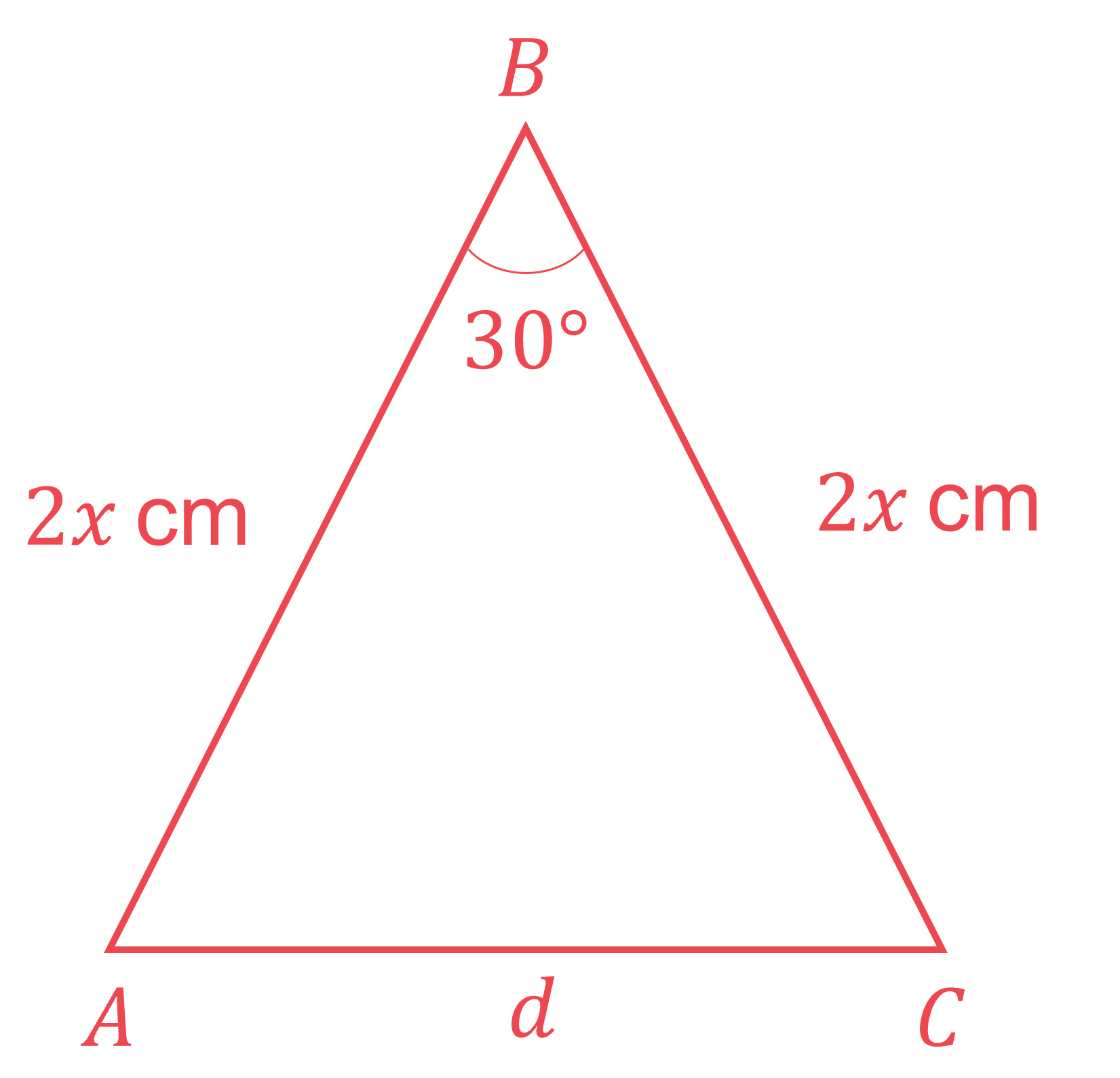
Use the cosine rule with a = d, b = 2x, c = 2x and A = 30°

$d^{2} = {(2 x)}^{2} + {(2 x)}^{2} - 2 (2 x) (2 x) \cos 30$

Simplify the powers and collect like terms

$\begin{array}{rcl} d^{2} & = & 4 x^{2} + 4 x^{2} - 8 x^{2} \cos 30 \\ d^{2} & = & 8 x^{2} - 8 x^{2} \cos 30 \end{array}$

Use the exact value of cos 30 and simplify
$d^{2} = 8 x^{2} - 8 x^{2} \times \frac{\sqrt{3}}{2} d^{2} = 8 x^{2} - 4 x^{2} \sqrt{3}$

Factorise out 4x² on the right-hand side

$d^{2} = 4 x^{2} (2 - \sqrt{3})$

Splitting the triangle into two right-angled triangles doesn't help with this question in a non-calculator paper (you do not know exact trig values for 15° or 75°)

Last updated: 6 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Right-Angled TrigonometryNext:3D Pythagoras & Trigonometry

Sine, Cosine Rule & Area of Triangles (AQA GCSE Further Maths)

Revision Note

Sine & Cosine Rules

What are the sine rule and cosine rule formulae?

What is the ambiguous case of the sine rule?

How do I know whether to use sine rule or cosine rule?

Examiner Tips and Tricks

Worked Example

Area of a Triangle

What is the area of a triangle formula?

Examiner Tips and Tricks

Worked Example

Applications of Trigonometry

How do I choose which rule or formula to use

What problems will I be asked to solve using trigonometry?

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Paul

Author: Dan Finlay