Right-Angled Trigonometry (AQA GCSE Further Maths): Revision Note
Exam code: 8365
Pythagoras
What is the Pythagorean theorem?
Pythagoras’ theorem is a formula that works for right-angled triangles only
It states that for any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the two shorter sides
The hypotenuse is the longest side in a right-angled triangle
It will always be opposite the right angle
If we label the hypotenuse c, and label the other two sides a and b, then Pythagoras’ theorem tells us that
How can we use Pythagoras’ theorem?
If you know two sides of any right-angled triangle you can use Pythagoras’ theorem to find the length of the third side
Substitute the values you have into the formula and either solve or rearrange
To find the length of the hypotenuse you can use:
To find the length of one of the other sides you can use:
or
Note that when finding the hypotenuse you should add inside the square root and when finding one of the other sides you should subtract inside the square root
Always check your answer carefully to make sure that the hypotenuse is the longest side
Note that Pythagoras’ theorem questions will rarely be standalone questions and will often be ‘hidden’ in other geometry questions
Examiner Tips and Tricks
Pythagoras' theorem pops up in lots of exam questions so bear it in mind whenever you see a right-angled triangle in an exam question!
Worked Example
Find an expression for the length , in terms of
.
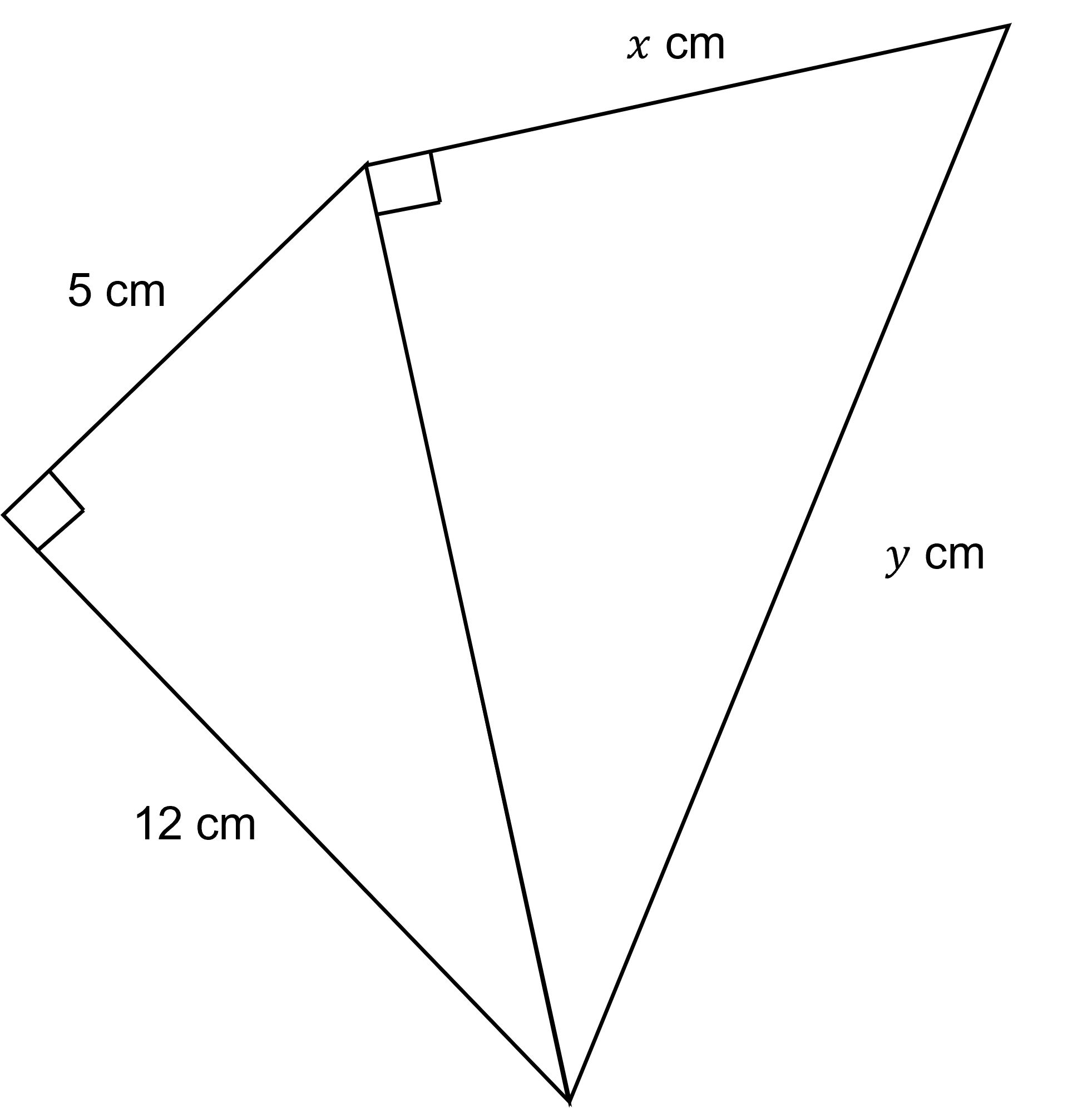
Use Pythagoras' theorem to find the hypotenuse of the right-angled triangle on the lef
Simplify this value
Write out Pythagoras' theorem for the right-angled triangle on the right, using the length found above of 13 cm
Make y the subject by square-rooting both sides
(you cannot square root each individual term)
No is needed as y is a length (positive)
Did this video help you?
SOHCAHTOA
What is trigonometry?
Trigonometry is the mathematics of angles in triangles
It looks at the relationship between side lengths and angles of triangles
It comes from the Greek words trigonon meaning ‘triangle’ and metron meaning ‘measure’
What are sin, cos and tan?
The three trigonometric functions Sine, Cosine and Tangent come from ratios of side lengths in right-angled triangles
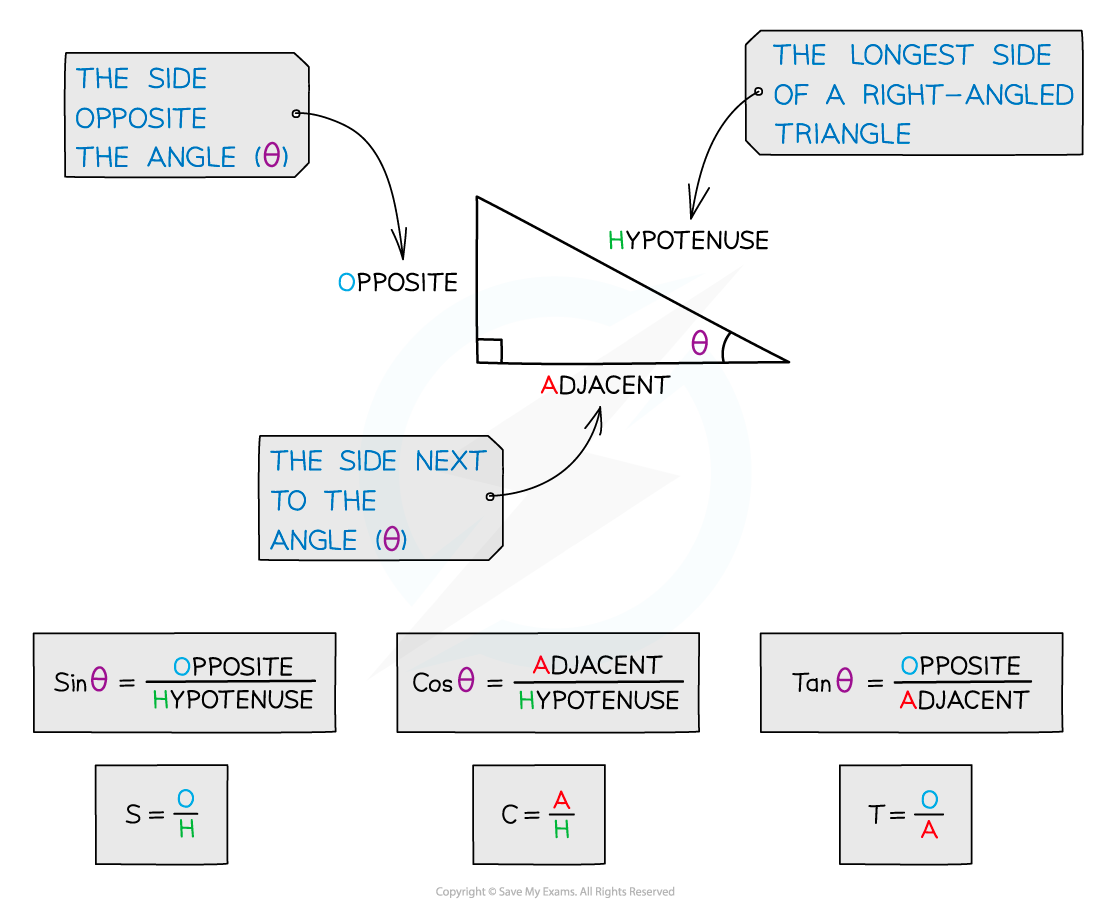
To see how the ratios work you must first label the sides of a right-angled triangle in relation to a chosen angle
The hypotenuse, H, is the longest side in a right-angled triangle
It will always be opposite the right angle
If we label one of the other angles θ, the side opposite θ will be labelled opposite, O, and the side next to θ will be labelled adjacent, A
The functions Sine, Cosine and Tangent are the ratios of the lengths of these sides as follows
What is SOHCAHTOA?
SOHCAHTOA is a mnemonic that is often used as a way of remembering which ratio is which
Sin is Opposite over Hypotenuse
Cos is Adjacent over Hypotenuse
Tan is Opposite over Adjacent
In a right-angled triangle, label one angle other than the right angle and label the sides of the triangles as follows

Note that θ is the Greek letter theta
O = opposite θ
A = adjacent (next to) θ
H = hypotenuse - 'H' is always the same, but 'O' and 'A' change depending on which angle we're calling θ
Using those labels, the three SOHCAHTOA equations are:
How can I use SOHCAHTOA to find missing lengths?
If you know the length of one of the sides of any right-angled triangle and one of the angles you can use SOHCAHTOA to find the length of the other sides
Always start by labelling the sides of the triangle with H, O and A
Choose the correct ratio by looking only at the values that you have and that you want
For example if you know the angle and the side opposite it (O) and you want to find the hypotenuse (H) you should use the sine ratio
Substitute the values into the ratio
Use your calculator to find the solution
How can I use SOHCAHTOA to find missing angles?
If you know two sides of any right-angled triangle you can use SOHCAHTOA to find the size of one of the angles
Missing angles are found using the inverse functions:
,
,
After choosing the correct ratio and substituting the values use the inverse trigonometric functions on your calculator to find the correct answer
Examiner Tips and Tricks
SOHCAHTOA (like Pythagoras) can only be used in right-angles triangles – for triangles that are not right-angled, you will need to use the Sine Rule or the Cosine Rule
Also, make sure your calculator is set to measure angles in degrees
Worked Example
Find the values of and
in the following triangles.
Give your answers to 3 significant figures.

To find , first label the triangle

We know A and we want to know O - that's TOA or
Multiply both sides by 9
Enter on your calculator
Round to 3 significant figures
To find , first label the triangle

We know A and H - that's CAH or
Use inverse cos to find
Enter on your calculator
Round to 3 significant figures
Did this video help you?
Exact trig values
What are exact values in trigonometry?
For certain angles the values of sin θ, cos θ and tan θ can be written exactly
This means using fractions and surds
You should be familiar with these values and be able to derive the values using geometry
You are expected to know the exact values of sin, cos and tan for angles of 0°, 30°, 45°, 60°, 90°, 180° and their multiples
The exact values you are expected to know are summarised here:

Note that the values of sin θ going from 0° to 90° match those of cos θ going from 90° to 0°
How are exact values in trigonometry derived?
There are two special right-angled triangles that can be used to derive all of the exact values you need to know
Consider a right-angles triangle with a hypotenuse of 2 units and a shorter side length of 1 unit
Using Pythagoras’ theorem the third side will be
The angles will be 90°, 60° and 30°
Using SOHCAHTOA gives…
Sin 60° =
Sin 30° =
Cos 60° =
Cos 30° =
Tan 60° =
Tan 30° =
=
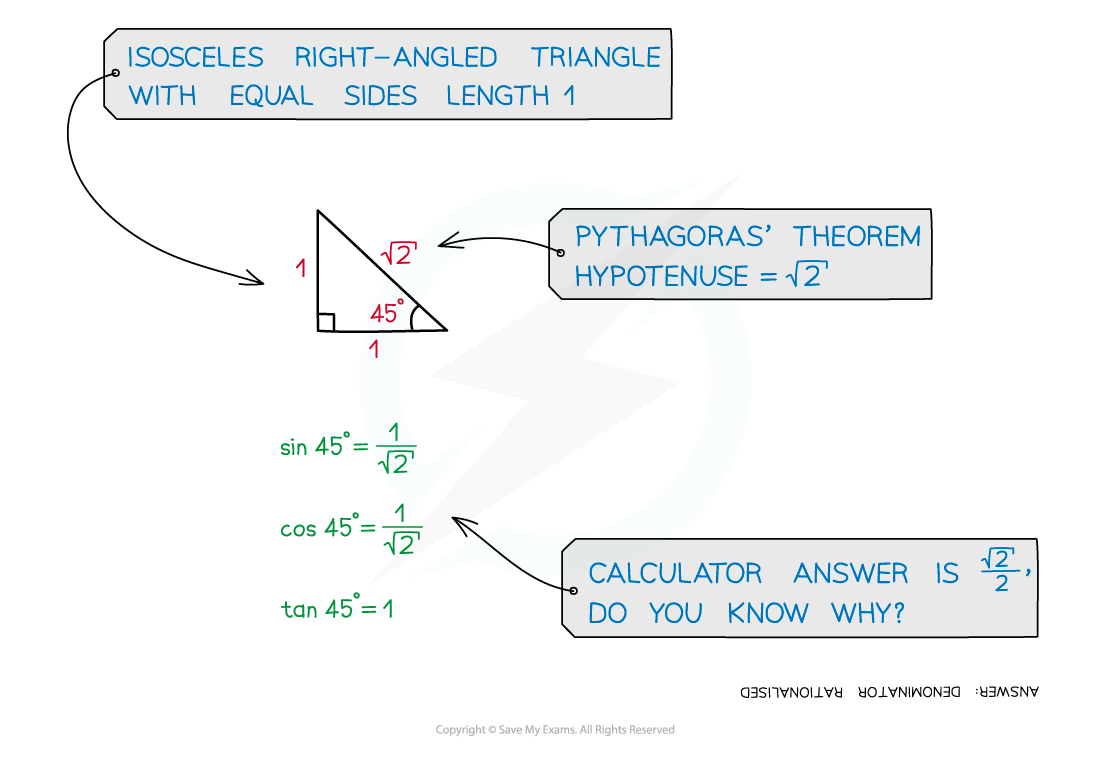
Consider an isosceles triangle with two equal side lengths (the opposite and adjacent) of 1 unit
Using Pythagoras’ theorem it will have a hypotenuse of
The two equal angles will be 45°
Using SOHCAHTOA gives…
Sin
Cos
Tan
= 1
Examiner Tips and Tricks
You will be expected to be comfortable using exact trig values for certain angles but it can be easy to muddle them up if you just try to remember them from a list
sketch the triangles and trig graphs on your paper so that you can use them as many times as you need to during the exam
sketch the triangles for the key angles
,
,
sketch the trig graphs for the key angles
,
,
,
,
Worked Example
Using an equilateral triangle of side length 2 units, derive the exact values for the sine, cosine and tangent of 60° and 30°.
Sketch the triangle and create two right angled triangles by drawing the line of symmetry through the middle.

Use Pythagoras' theorem to find the vertical height of the triangle.
Use SOHCAHTOA to find the trig ratios for 30° and 60°.
Sin 60° = Sin 30° =
Cos 60° = Cos 30° =
Tan 60° = Tan 30° =

Unlock more, it's free!
Did this page help you?