3D Pythagoras & Trigonometry (AQA GCSE Further Maths): Revision Note
Exam code: 8365
3D Pythagoras & trigonometry
What skills will I need to solve 3D problems involving Pythagoras & trigonometry?
Pythagoras’ Theorem helps us find missing side lengths of a right-angled triangle;
It is also frequently used for finding the distance/length of a line
SOHCAHTOA is an acronym for the three trigonometric ratios that connect angles (θ) and sides (opposite, hypotenuse and adjacent) in a right-angled triangle
sine – SOH –
cosine – CAH –
tangent – TOA –
The hardest problems may involve sine rule, cosine rule and/or area of a triangle
sine rule -
cosine rule -
area of a triangle -
Other skills involving angles may also be involved
e.g. bearings, angles of elevation and depression, angles in parallel and perpendicular lines
How does Pythagoras work in 3D?
3D shapes can often be broken down into several 2D shapes
For example nets and surface area
With Pythagoras’ Theorem problems you will be specifically looking for right‑angled triangles
The right-angled triangles you need will have two known sides and one unknown side

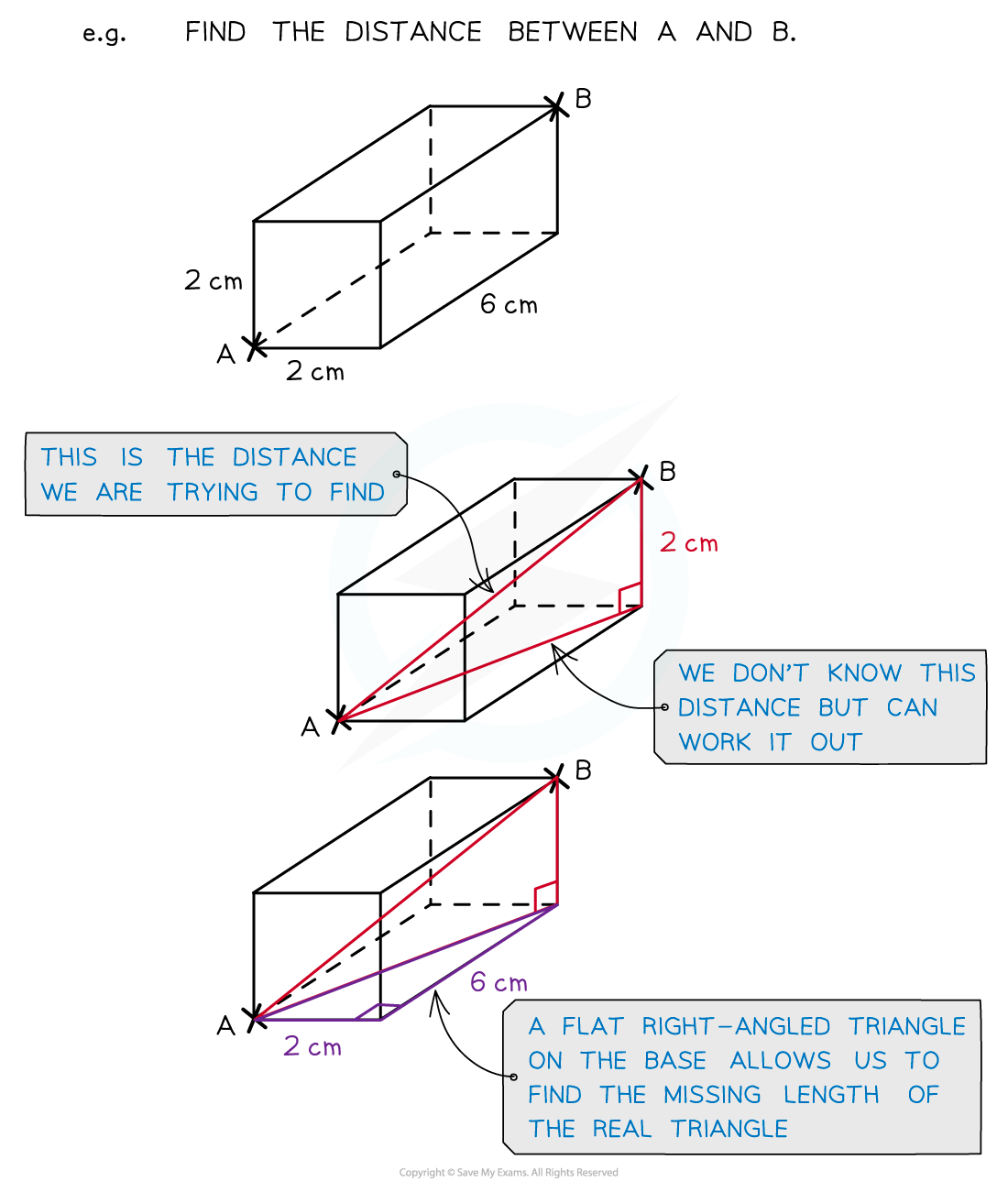
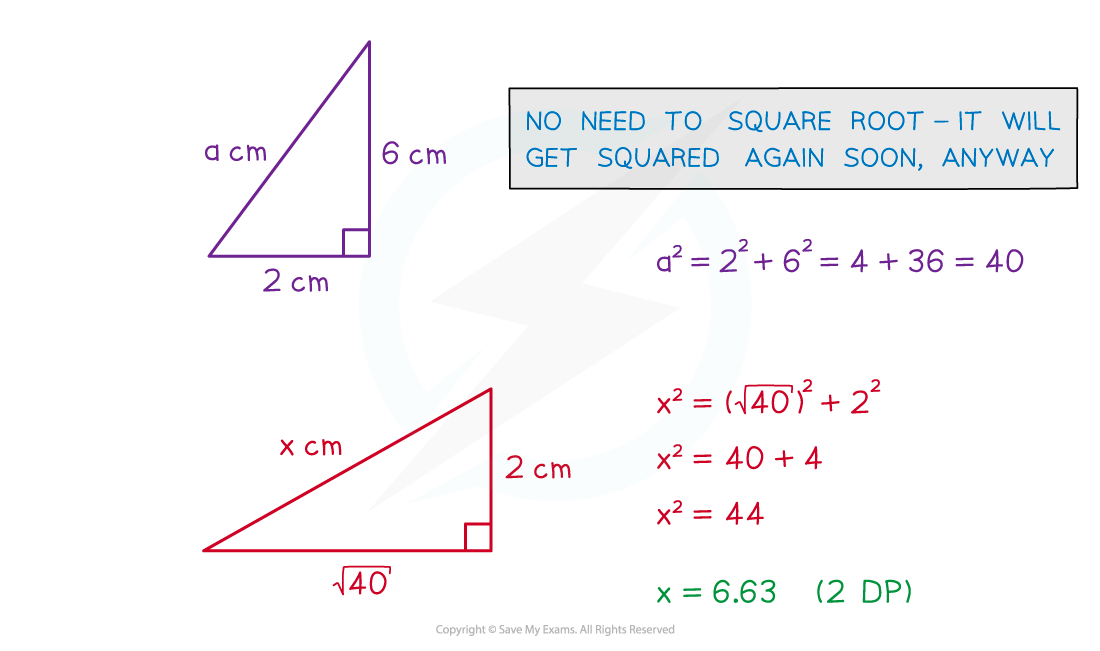
There is a 3D version of the Pythagoras’ Theorem formula
However it is usually far easier to see a problem by splitting it into two or more 2D problems

How does trigonometry work in 3D?
Again look for a combination of triangles that would lead to the missing angle or side
Ideally look for right-angled triangles so SOHCAHTOA can be used
Failing that, look for 'pairs' to use sine rule and 'two sides and the angle between them' for cosine rule
The angle you are working with can be awkward in 3D
The angle between a line and a plane is not obvious
If unsure, put a point on the line and draw a new line to the plane
This should create a right-angled triangle
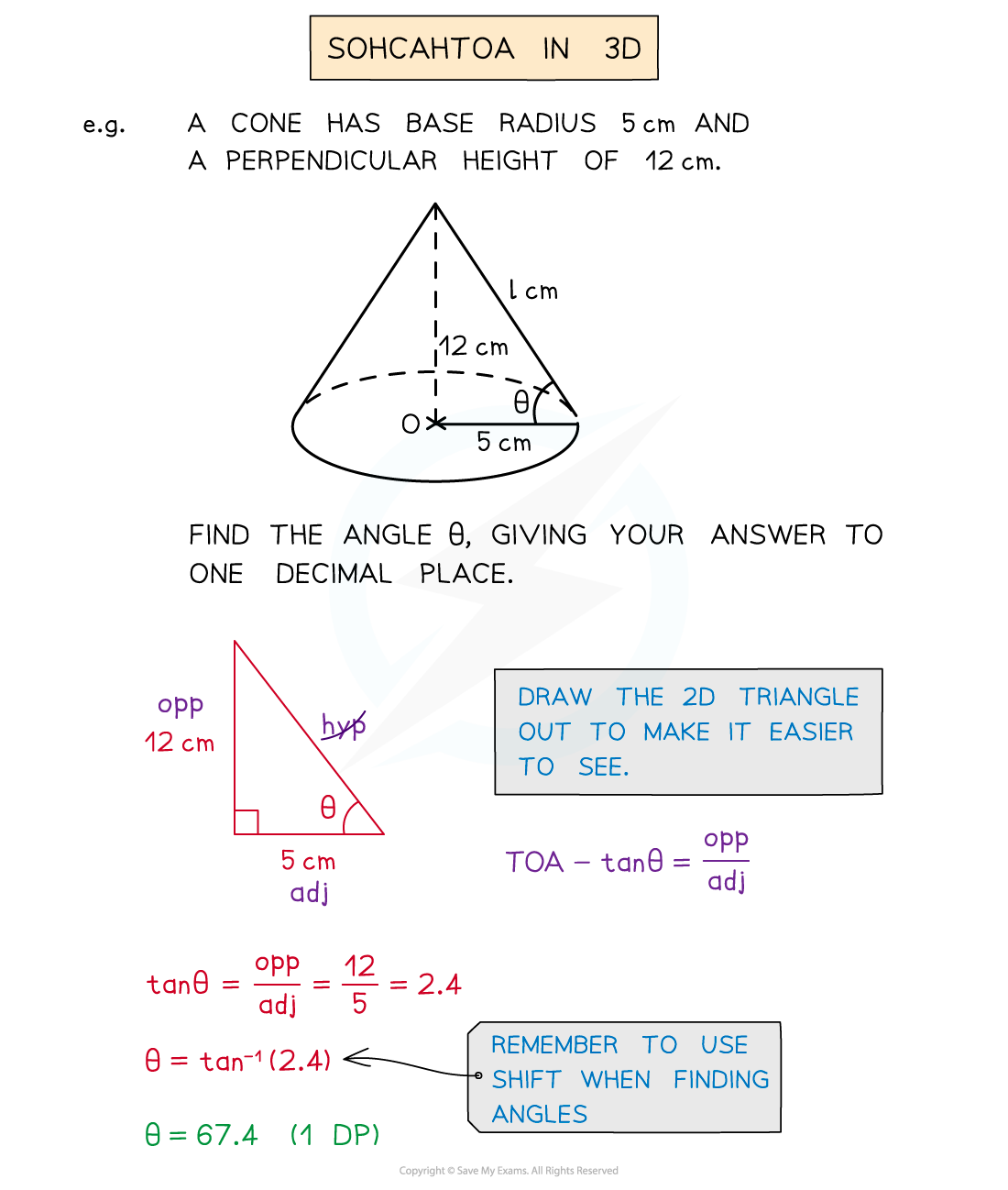
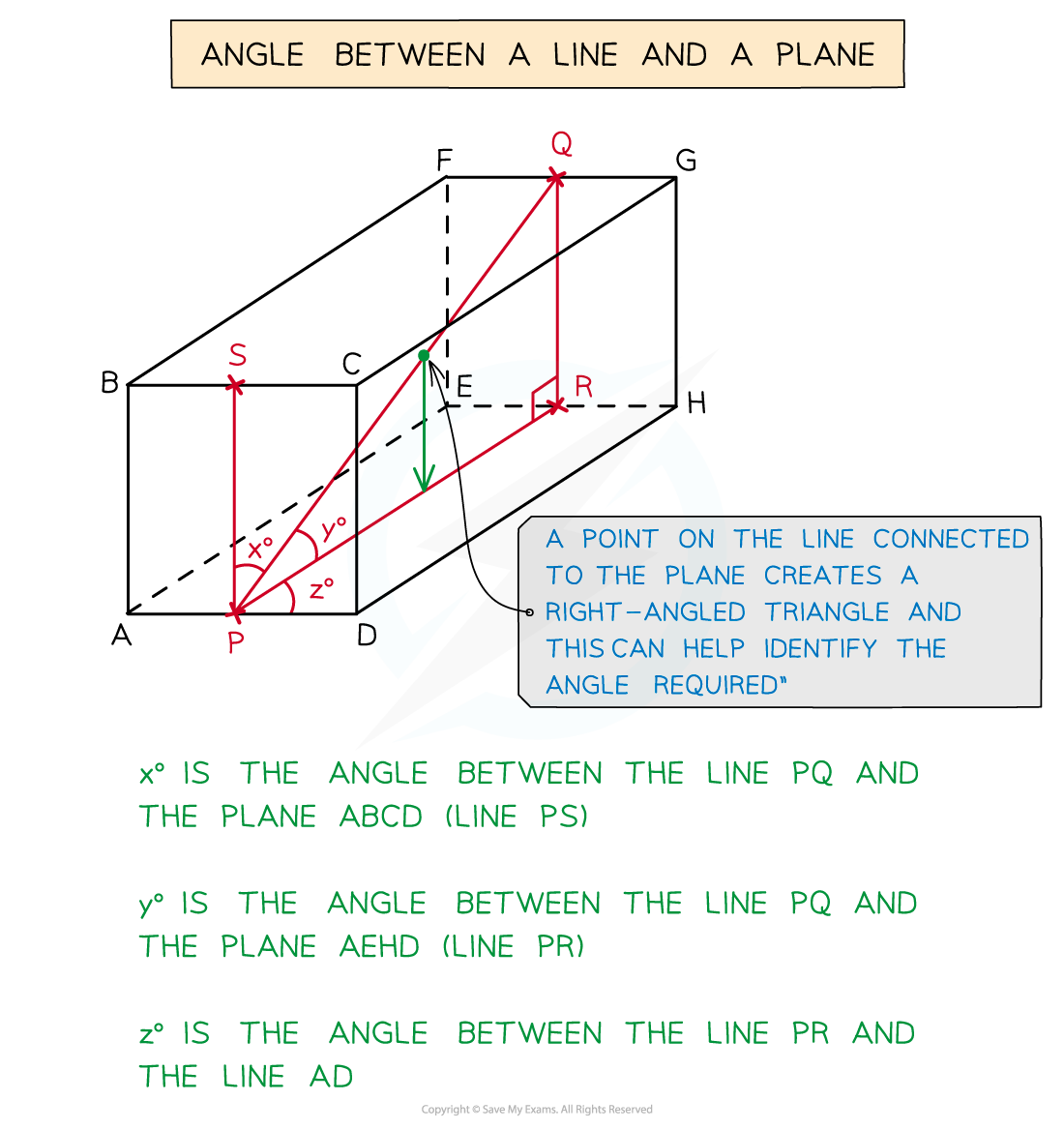
Once you have your 2D triangle(s) you can begin to solve problems

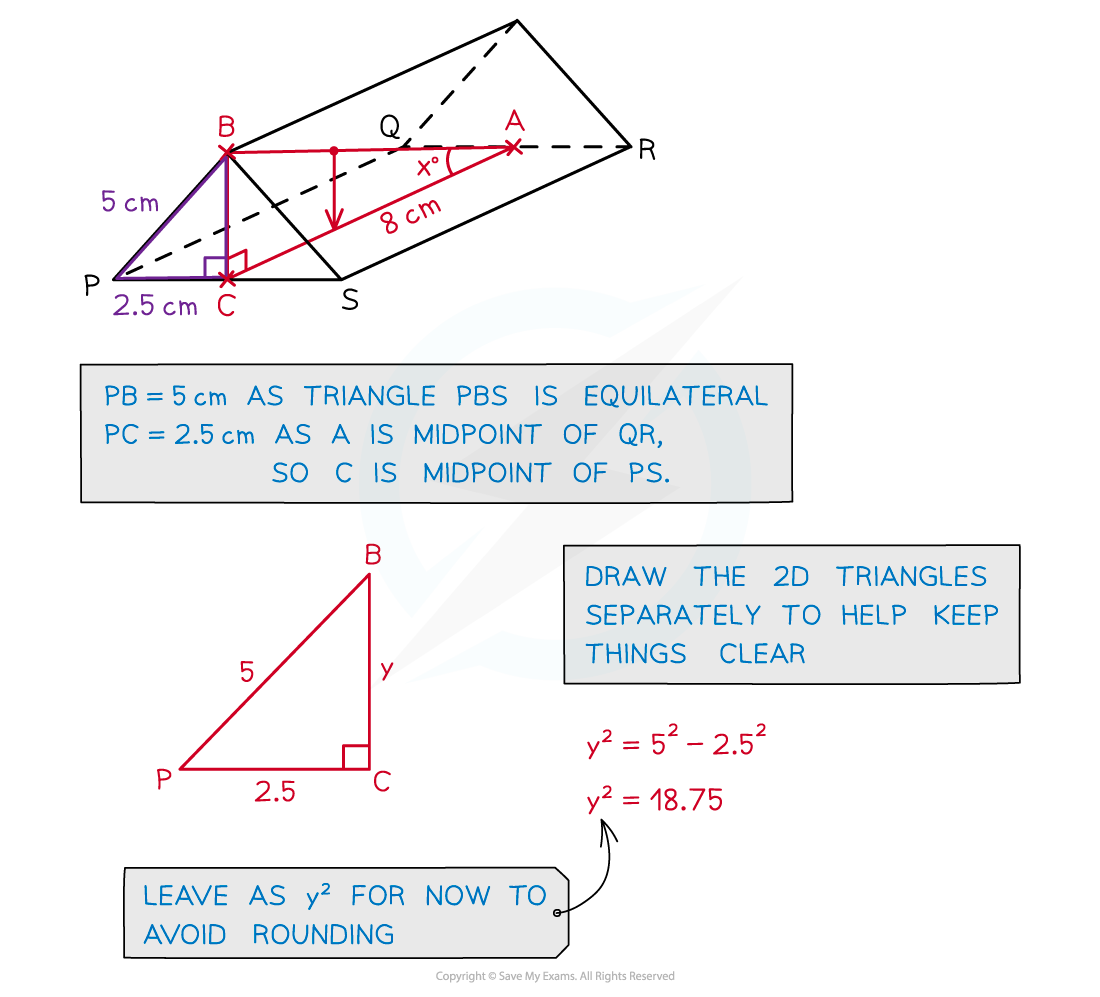
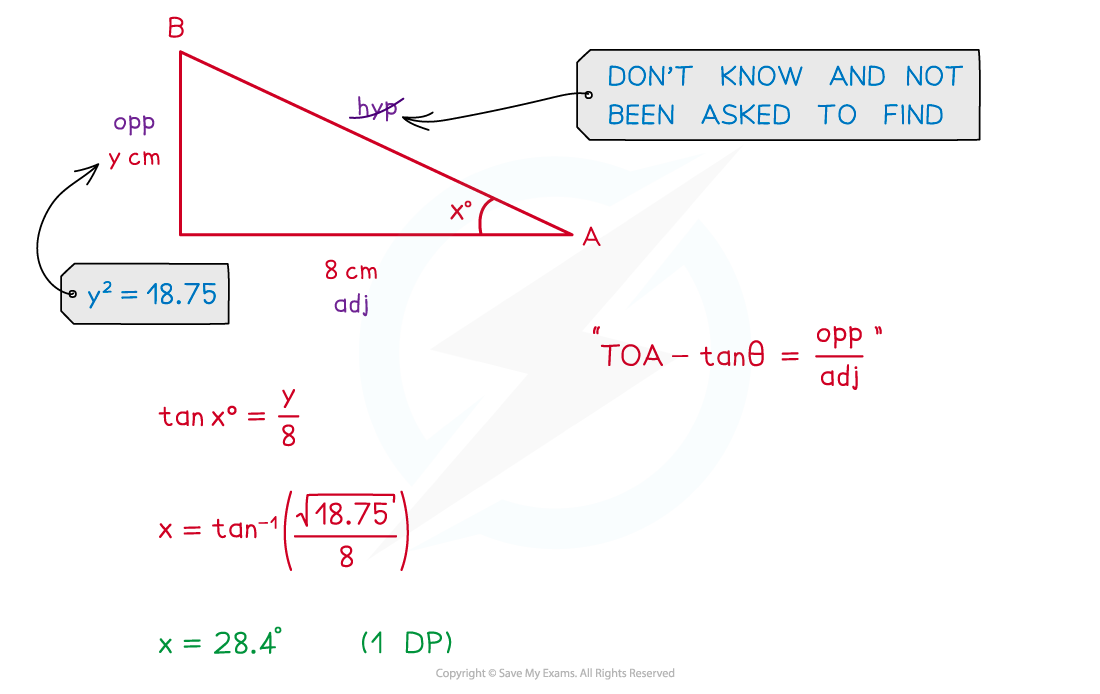
Examiner Tips and Tricks
Add lines/triangles/etc to any given diagram to help you see the problem
If no diagram is given, sketch your own!
Draw any 2D triangles separately as a 3D diagram can get hard to follow
Worked Example
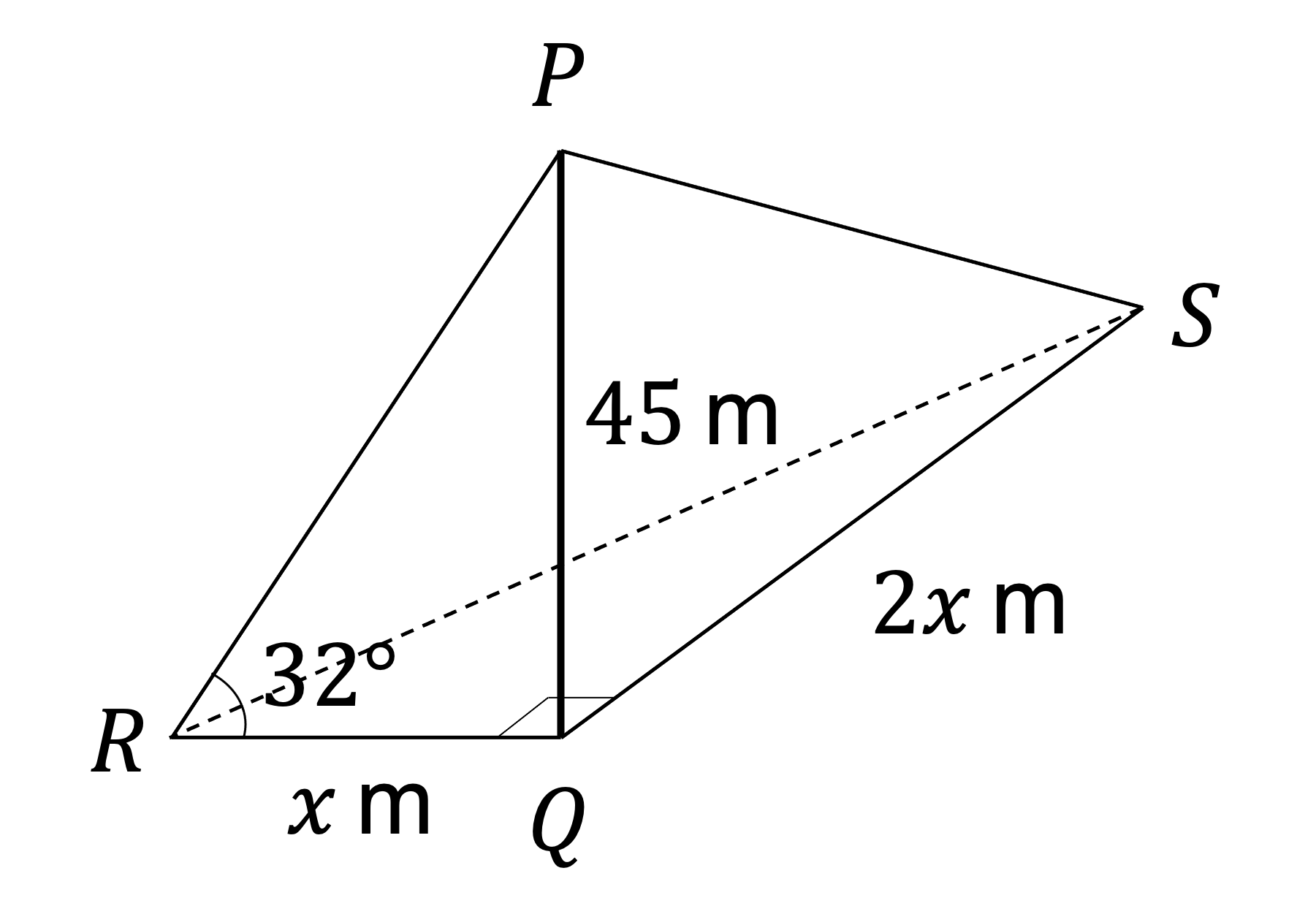
The diagram shows a vertical tree, PQ.
The angle of elevation of the top of the tree from the point R on the ground, x m due east of the tree, is 32°.
The point S lies on the ground, 2x m due north of the tree.
The distance between the points R and S is 45 m.
Find the height of the tree, giving your answer to the nearest 10 cm.
Draw triangle RQS as a 2D diagram
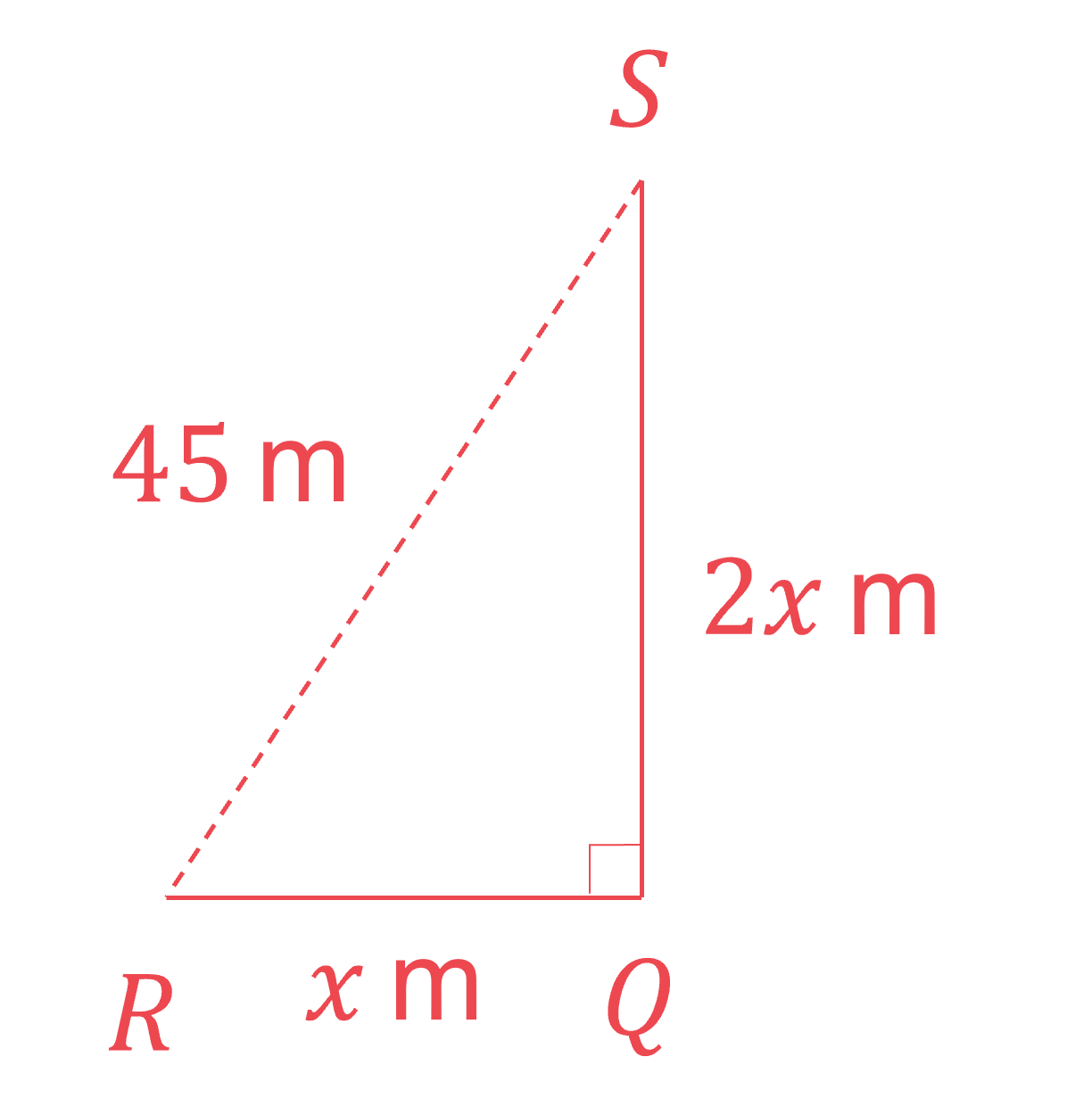
Use Pythagoras' theorem to find x
Draw triangle RQP and include 9√5 on the diagram
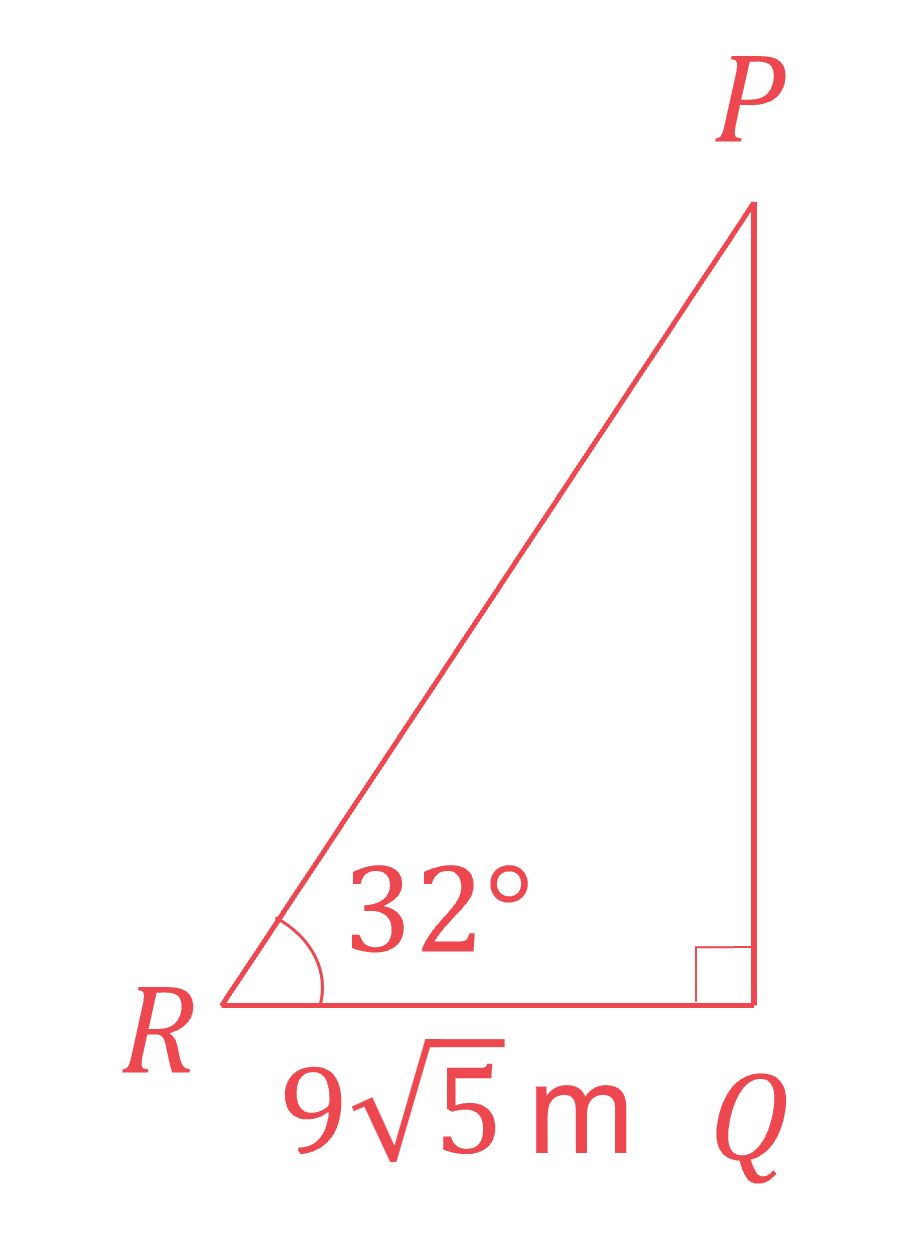
Use SOHCAHTOA to find the length P
Work out this value using a calculato
PQ = 12.575...
Give the answer to the nearest 10 cm (the same as one decimal place)
The height of the tree is 12.6 m
Worked Example
A small wedge consists of three rectangular faces and two triangular faces as shown in the diagram below.
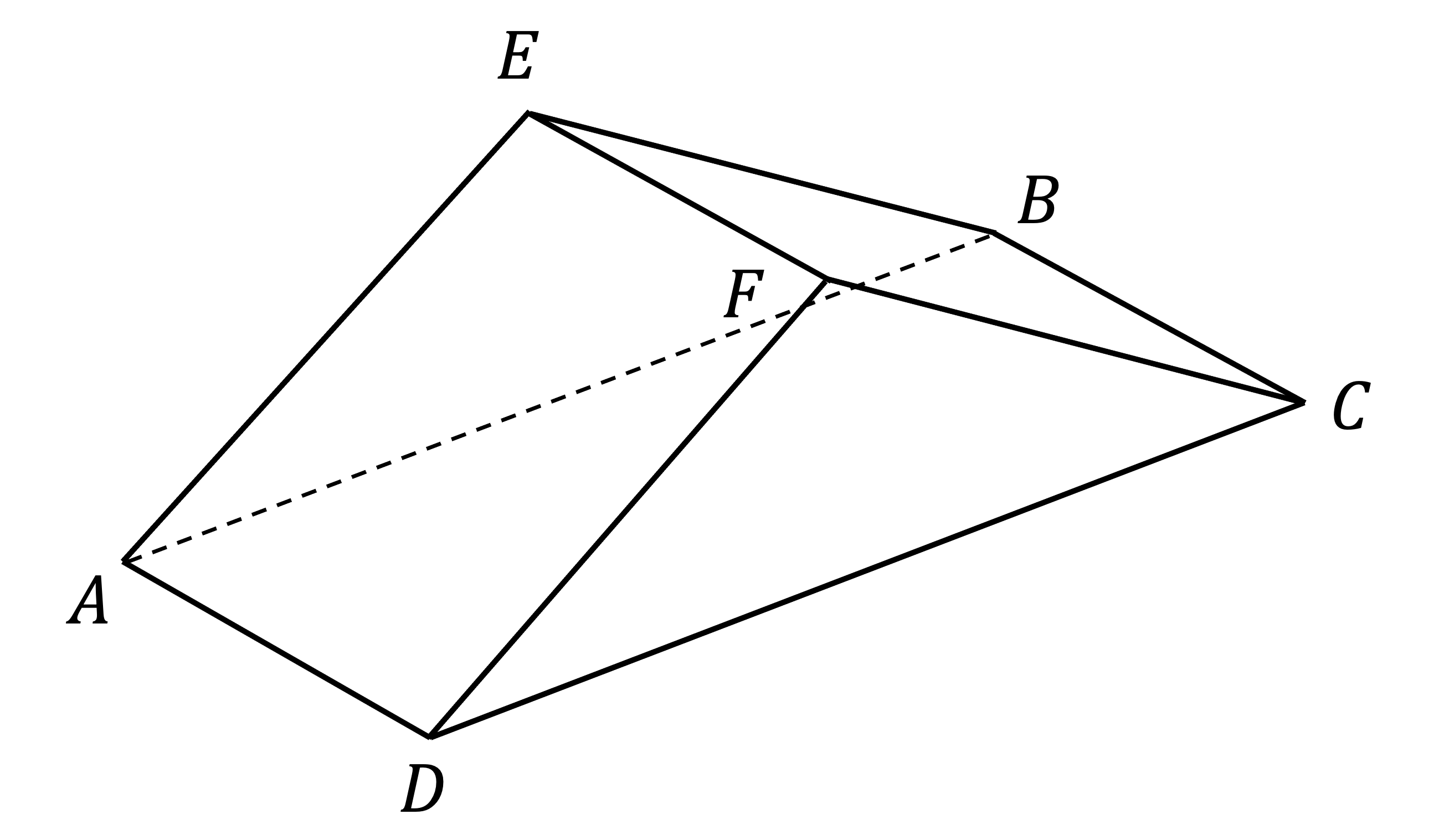
Rectangles AEFD and BEFC are congruent.
The base of the wedge, rectangle ABCD lies horizontally.
The maximum vertical height of the wedge is 5 cm and the length of CD is 12 cm.
Find the angle between the planes ABCD and AEFD, giving your answer to one decimal place.
As rectangles AEFD and BEFC are congruent, lengths DF and FC will be equal and so triangle CDF is isosceles
This will also mean the maximum height of the wedge (at point F) lies directly above the midpoint of CD
The angle between the planes required is angle CDF
We can create a 2D right-angled triangle to help solve the problem
Using M as the midpoint of CD and as angle CDF
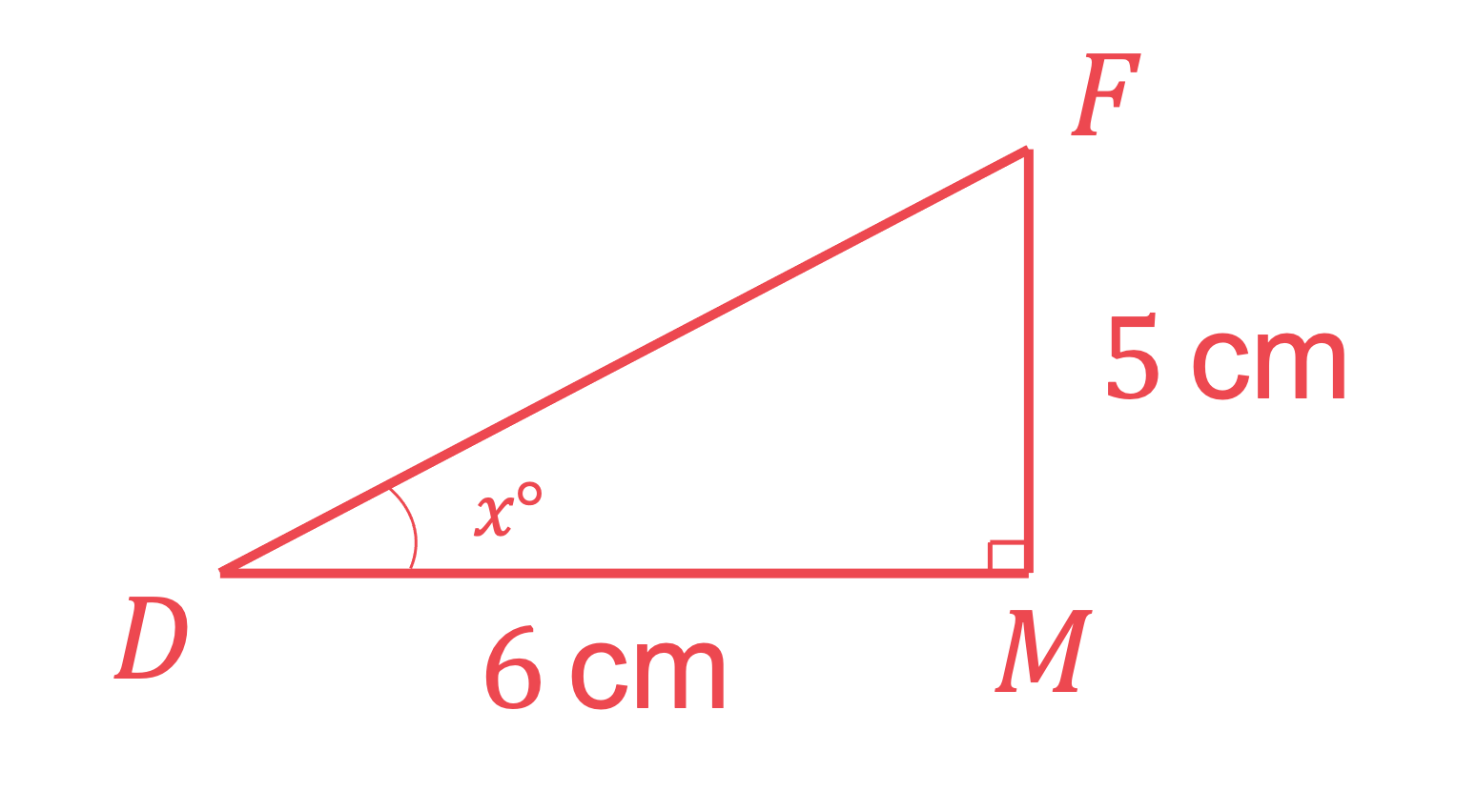
Use SOHCAHTOA to set up an equation for
Use inverse tan to find
Round to one decimal place for the final answer
The angle between planes ABCD and AEFD is 39.8° (1 d.p.)

Unlock more, it's free!
Did this page help you?