GCSEFurther MathsAQARevision Notes6. GeometryTrigonometric Graphs & EquationsTrigonometric Identities

Trigonometric Identities (AQA GCSE Further Maths): Revision Note

Last updated

Trigonometric Identities

What is a trigonometric identity?

  • Trigonometric identities (trig identity) are statements that are true for all values (of x or theta)

    • They are used to help simplify trigonometric equations before solving them

    • Sometimes you may see identities written with the symbol ≡

      • This means 'identical to'

What trigonometric identities do I need to know?

  • There are two trig identities you need to know and use

    • bold tan bold space bold italic theta bold identical to fraction numerator bold sin bold space bold theta over denominator bold cos bold space bold theta end fraction

      • This is the identity for tan θ

    • bold sin to the power of bold 2 space bold italic theta bold plus bold cos to the power of bold 2 bold space bold italic theta bold identical to bold 1

      • You may see this referred to as the Pythagorean identity

      • Note that the notation sin space squared theta is the same as left parenthesis sin space theta right parenthesis to the power of space 2 end exponent

      • Similar for cos squared space theta

  • Both identities are given on the formulae sheet

Where do the trigonometric identities come from?

  • You do not need to know the proof for these identities

    • However it is a good idea to know where they come from

  • The identity for tan space theta can be seen by diving sin space theta by cos space theta using their definitions from SOHCAHTOA

    • fraction numerator sin space theta over denominator cos space theta end fraction equals fraction numerator O over H over denominator A over H end fraction equals O over A equals tan space theta

  • The Pythagorean identity can be seen by considering a right-triangle with a hypotenuse of 1

    • Then using Pythagoras' theorem (a squared equals b squared plus c squared, where a is the hypotenuse)

      • 1 squared equals O squared plus A squared

      • From SOHCAHTOA, table row cell sin space theta end cell equals cell O over H equals O over 1 comma space space therefore O equals sin space theta end cell end table and cos space theta equals A over H equals A over 1 comma space therefore A equals cos space theta

      • And so sin squared space theta plus cos squared space theta blank equals blank 1

How are the trigonometric identities used?

  • Most commonly trig identities are used to rewrite an equation

  • Rearrangements of the Pythagorean identity are very useful for rewriting equations

    • This allows us to write equations in terms of sine or cosine only (making them easier to solve)

      • sin to the power of 2 space end exponent theta equals blank 1 minus space cos to the power of 2 space end exponent theta

      • cos to the power of 2 space end exponent theta equals blank 1 minus space sin to the power of 2 space end exponent theta

Examiner Tips and Tricks

  • If you are asked to show that one expression is identical (≡) to another, look for anything that has gone missing!

    • e.g.  if tan space x is in the original expression but not the 'answer' it must have been replaced by fraction numerator sin space x over denominator cos space x end fraction

Worked Example

Show that the equation 2 sin squared space x minus cos space x equals 0 can be written in the form a cos squared space x plus b cos space x plus c equals 0, where a, b and c are integers to be found.

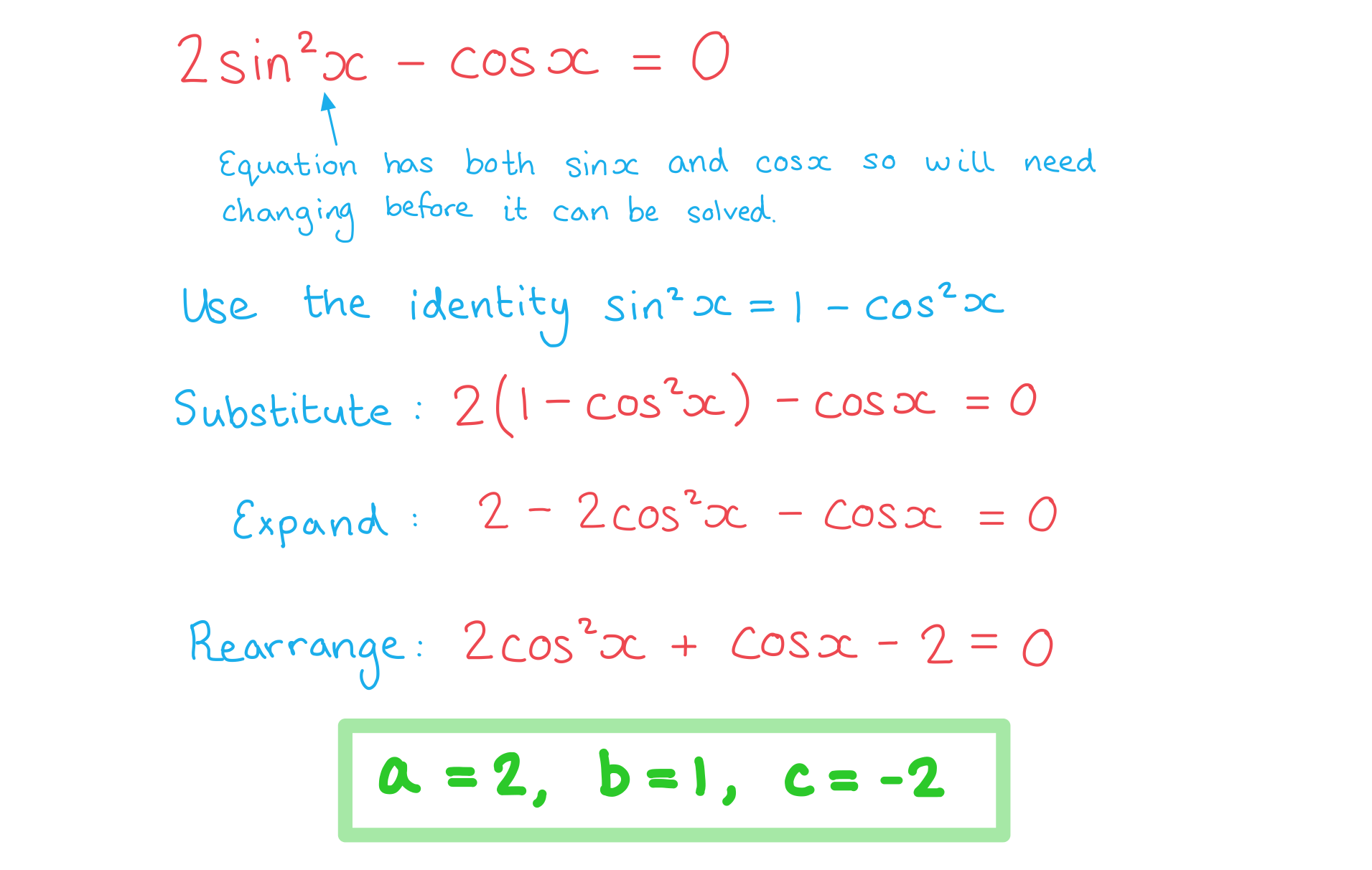
aa-sl-3-6-1-we-solutions-1

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Trigonometric GraphsNext:Solving Trig Equations
Download notes on Trigonometric Identities