Differentiating Powers of x (AQA GCSE Further Maths)

Revision Note

Test yourself

Written by: Jamie Wood

Reviewed by: Dan Finlay

Differentiating Powers of x

What is differentiation?

Differentiation is the process of finding an expression of the derivative (gradient function) from the equation of a curve
- The equation of the curve is written $y = . . .$ and the gradient function is written $\frac{d y}{d x} = . . .$

How do I differentiate powers of x?

Powers of $x$ are differentiated according to the following formula:
- If $y = a x^{n}$ then $\frac{d y}{d x} = a n x^{n - 1}$
  - e.g. If $y = 4 x^{3}$ then $\frac{d y}{d x} = 4 \times 3 \times x^{3 - 1} = 12 x^{2}$
  - you "bring down the power" then "subtract one from the power"
Don't forget these two special cases:
- If $y = a x$ then $\frac{d y}{d x} = a$
  - e.g. If $y = 6 x$ then $\frac{d y}{d x} = 6$
- If $y = a$ then $\frac{d y}{d x} = 0$
  - e.g. If $y = 5$ then $\frac{d y}{d x} = 0$
- These allow you to differentiate linear terms in $x$ and constants
Functions involving fractions with denominators in terms of $x$ will need to be rewritten as negative powers of $x$ first
- e.g. If $y = \frac{4}{x}$ then rewrite as $y = 4 x^{- 1}$ and differentiate

How do I differentiate sums and differences of powers of x?

The formulae for differentiating powers of $x$ work for a sum or difference of powers of $x$
- e.g. If $y = 5 x^{4} + 3 x^{- 2} + 4$ then
  $\frac{d y}{d x} = 5 \times 4 x^{4 - 1} + 3 \times (- 2) x^{- 2 - 1} + 0$
  $\frac{d y}{d x} = 20 x^{3} - 6 x^{- 3}$
- This is sometimes referred to differentiating 'term-by-term'
Products and quotients (divisions) cannot be differentiated in this way so they need expanding/simplifying first
- e.g. If $y = (2 x - 3) (x^{2} - 4)$ then expand to $y = 2 x^{3} - 3 x^{2} - 8 x + 12$ which is a sum/difference of powers of $x$ and can then be differentiated

What can I do with derivatives (gradient functions)?

The derivative can be used to find the gradient of a function at any point
- The gradient of a function at a point is equal to the gradient of the tangent to the curve at that point
- A question may refer to the gradient of the tangent

Examiner Tips and Tricks

Don't try to do too many steps in your head; write the expression in a format that you can differentiate before you actually differentiate it
- e.g. $y = \frac{1}{x^{4}} + \frac{2}{x^{3}}$ can be rewritten as $y = x^{- 4} + 2 x^{- 3}$ which is then far easier to differentiate

Worked Example

Find the derivative of

(a) $\begin{matrix} \end{matrix}$ $y = 5 x^{3} + 2 x + \frac{3}{x^{2}} + 8$

Rewrite the $\frac{3}{x^{2}}$ term

$y = 5 x^{3} + 2 x + 3 x^{- 2} + 8$

Apply the rule for differentiating powers ( $y = a x^{n}, \frac{d y}{d x} = a n x^{n - 1}$ ) and apply the special cases for the terms $2 x$ and 8 ( $y = a x, \frac{d y}{d x} = a$ and $y = a, \frac{d y}{d x} = 0$ )

$\frac{d y}{d x} = 15 x^{2} + 2 - 6 x^{- 3}$

Unless a question specifies there is not usually a need to rewrite/simplify the answer

$\frac{d y}{d x} = 15 x^{2} + 2 - \frac{6}{x^{3}}$

(b) $y = {(2 x + 3)}^{2}$

This is a product of two (equal) brackets so cannot be differentiated directly
Expand the brackets to get an expression in powers of $x$
Take time to get the expansion correct, writing stages out in full if necessary

$\begin{array}{rcl} y & = & (2 x + 3) (2 x + 3) \\ y & = & 4 x^{2} + 6 x + 6 x + 9 \\ y & = & 4 x^{2} + 12 x + 9 \end{array}$

Differentiate 'term-by-term', looking out for those special cases

$\frac{d y}{d x} = 8 x + 12$

There is a factor of 4 but there is no demand to factoise the final answer in the question

$\frac{d y}{d x} = 8 x + 12$

This is a quotient so cannot be differentiated directly
Spot the single denominator which means we can split the fraction by the two terms on the numerator

$y = \frac{8 x^{6}}{2 x^{4}} - \frac{x^{3}}{2 x^{4}}$

Simplify using the laws of indices

$y = 4 x^{6 - 4} - \frac{1}{2} x^{3 - 4} y = 4 x^{2} - \frac{1}{2} x^{- 1}$

Each term is now a power of $x$ , so differentiate 'term-by-term'

$\frac{d y}{d x} = 8 x + \frac{1}{2} x^{- 2}$

There is demand to simplify or write the answer in a particular form

$\frac{d y}{d x} = 8 x + \frac{1}{2} x^{- 2}$

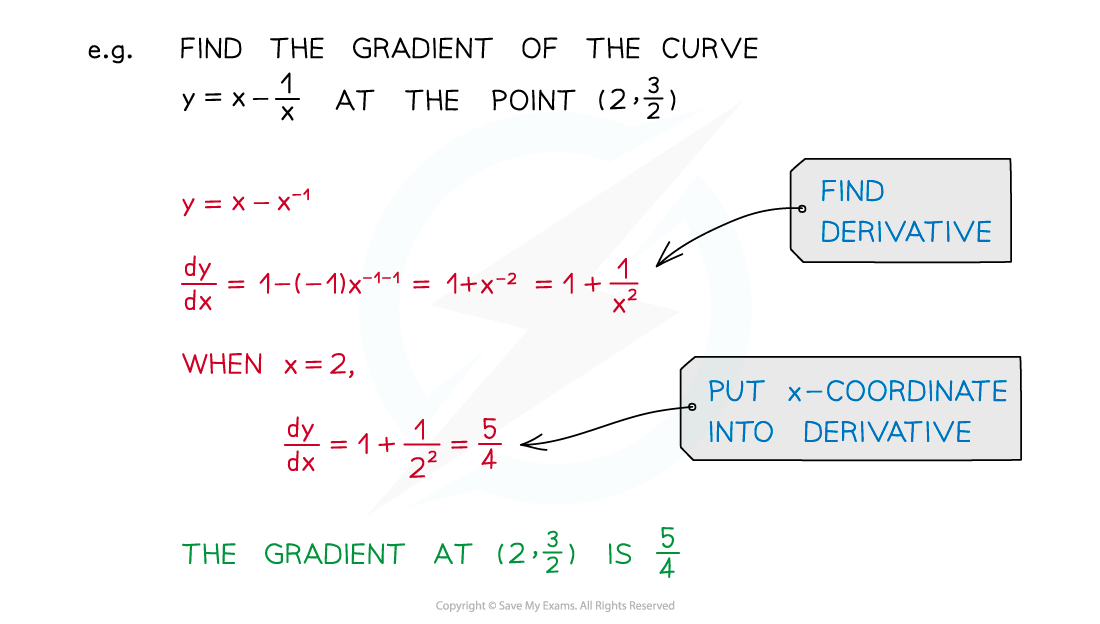
Finding Gradients of Curves

Using the derivative to find the gradient of a curve

To find the gradient of a curve, at any point on the curve, substitute the x‑coordinate of the point into the derivative $\frac{d y}{d x}$

Grad Tang Norm Illustr 1, A Level & AS Maths: Pure revision notes

Examiner Tips and Tricks

Read the question carefully; sometimes you are given $\frac{d y}{d x}$ and so don't need to differentiate initially - don't just automatically differentiate the first thing you see!
The following mean the same thing:
- "Find the gradient of the curve at $x = 2$ "
- "Find the gradient of the tangent at $x = 2$ "
  - the tangent gradient = curve gradient at that point
- "Find the rate of change of y with respect to x at $x = 2$ "

Worked Example

A curve has the equation $y = \frac{4}{3} x^{3} + 3 x - 8$ .

(a) Find the gradient of the curve when $x = 2$ .

$y$ is already in a form that can be differentiated

$\frac{d y}{d x} = 4 x^{2} + 3$

Substitute $x = 2$ into $\frac{d y}{d x}$

$\frac{d y}{d x} = 4 \times 2^{2} + 3 = 19$

The gradient of the curve at $x = 2$ is 19

(b)

Work out the possible values of $x$ for which the rate of change of $y$ with respect to $x$ is 4.

"Rate of change" is another way of describing the derivate

$\begin{array}{rcl} \frac{d y}{d x} & = & 4 \\ 4 x^{2} + 3 & = & 4 \end{array}$

Solve this equation to find $x$
Note that it is quadratic equation so it could have up to two solutions
The question refers to 'values' implying there is (or could be) more than one value for $x$

$\begin{array}{rcl} 4 x^{2} & = & 1 \\ x^{2} & = & \frac{1}{4} \\ x & = & \pm \sqrt{\frac{1}{4}} \\ x & = & \pm \frac{1}{2} \end{array}$

The possible values of $x$ , that give a rate of change of 4, are $x = \frac{1}{2}$ and $x = - \frac{1}{2}$

Last updated: 5 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Definition of GradientNext:Tangents & Normals

Differentiating Powers of x (AQA GCSE Further Maths)

Revision Note

Differentiating Powers of x

What is differentiation?

How do I differentiate powers of x?

How do I differentiate sums and differences of powers of x?

What can I do with derivatives (gradient functions)?

Examiner Tips and Tricks

Worked Example

Finding Gradients of Curves

Using the derivative to find the gradient of a curve

Examiner Tips and Tricks

Worked Example

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Jamie Wood

Author: Dan Finlay