Definition of Gradient (AQA GCSE Further Maths): Revision Note

Definition of Gradient

What is the gradient of a curve?

• At a given point the gradient of a curve is defined as the gradient of the tangent to the curve at that point

• A tangent to a curve is a line that just touches the curve at one point but doesn't cut the curve at that point

• A tangent may cut the curve somewhere else on the curve

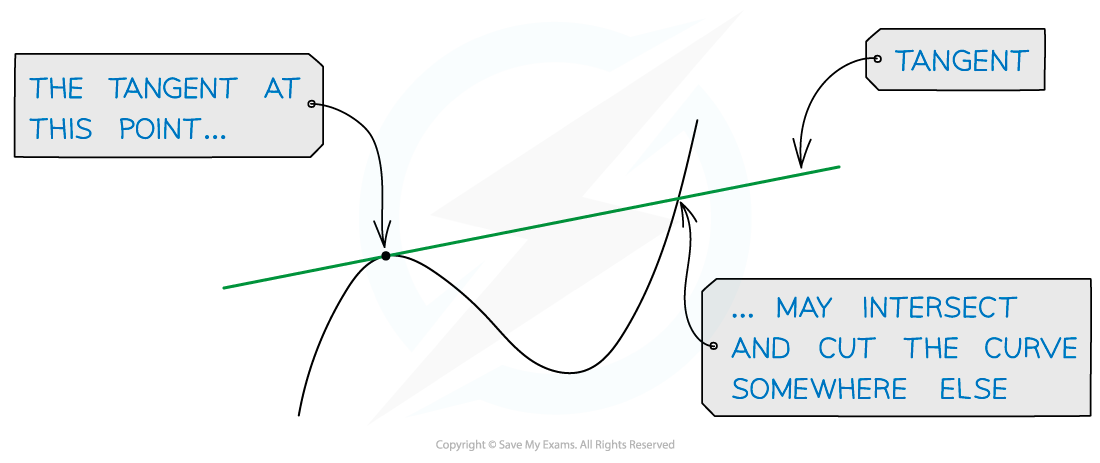
• It is only possible to draw one tangent to a curve at any given point

• Note that unlike the gradient of a straight line, the gradient of a curve is constantly changing

What is a derivative?

• Calculus is about rates of change

  • the way a car’s position on a road changes is its speed (velocity)

  • the way the car’s speed changes is its acceleration

• The gradient (rate of change) of a (non-linear) function varies with 

• The derivative of a function is a function that relates the gradient to the value of 

• The derivative is also called the gradient function