Stationary Points & Turning Points (AQA GCSE Further Maths)

Revision Note

Test yourself

Written by: Roger B

Reviewed by: Dan Finlay

Stationary Points & Turning Points

What are stationary points?

A stationary point is any point on a curve where the gradient is zero
To find stationary points of a curve

Step 1
Find the first derivative $\frac{d y}{d x}$

Step 2
Solve $\frac{d y}{d x} = 0$ to find the $x$ -coordinates of any stationary points

Step 3
Substitute those $x$ -coordinates into the equation of the curve to find the corresponding $y$ -coordinates

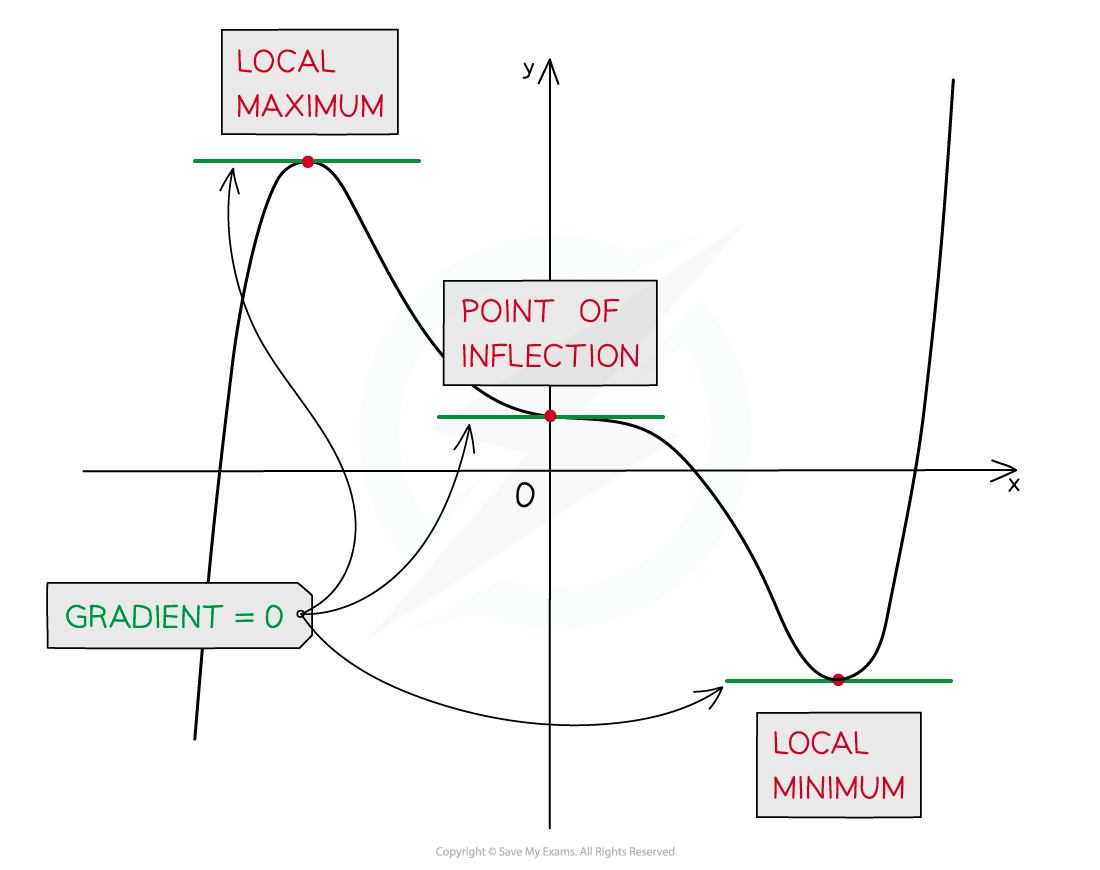
A stationary point may be either a local minimum, a local maximum, or a point of inflection

Stat Point Illustr 1, A Level & AS Maths: Pure revision notes

Stationary points on quadratics

The graph of a quadratic function only has a single stationary point
For a positive quadratic this is the minimum; for a negative quadratic it is the maximum
- No need to talk about 'local' here, as it is the overall minimum/maximum for the whole curve

Stationary Points min max for parabola illustr, A Level & AS Maths: Pure revision notes

The y value/coordinate of the stationary point is therefore the minimum or maximum value of the quadratic function
For quadratics especially, minimum and maximum points are often referred to as turning points

How do I determine the nature of stationary points on other curves?

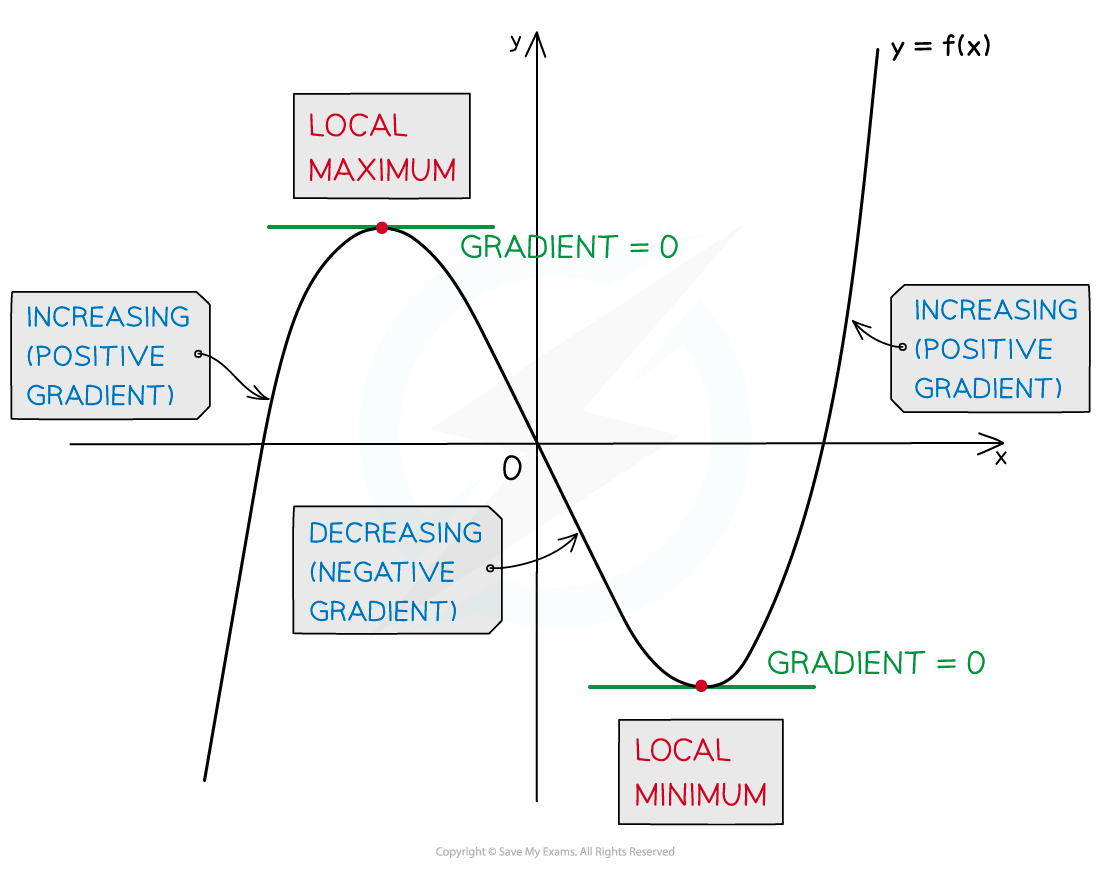
For a graph there are two ways to determine the nature of its stationary points
Method A
- Compare the signs of the first derivative, $\frac{d y}{d x}$ , (positive or negative) a little bit to either side of the stationary point
- (After completing Steps 1 - 3 above to find the stationary points)

Step 4
For each stationary point find the values of the first derivative a little bit 'to the left' (i.e. for a slightly smaller x value) and a little bit 'to the right' (i.e. for a slightly larger x value) of the stationary point

Stat Points left right proviso, A Level & AS Maths: Pure revision notes

Step 5
Compare the signs (positive or negative) of the derivatives on the left and right of the stationary point

If the derivatives are negative on the left and positive on the right, the point is a local minimum (a u-shape)
If the derivatives are positive on the left and negative on the right, the point is a local maximum (an n-shape)
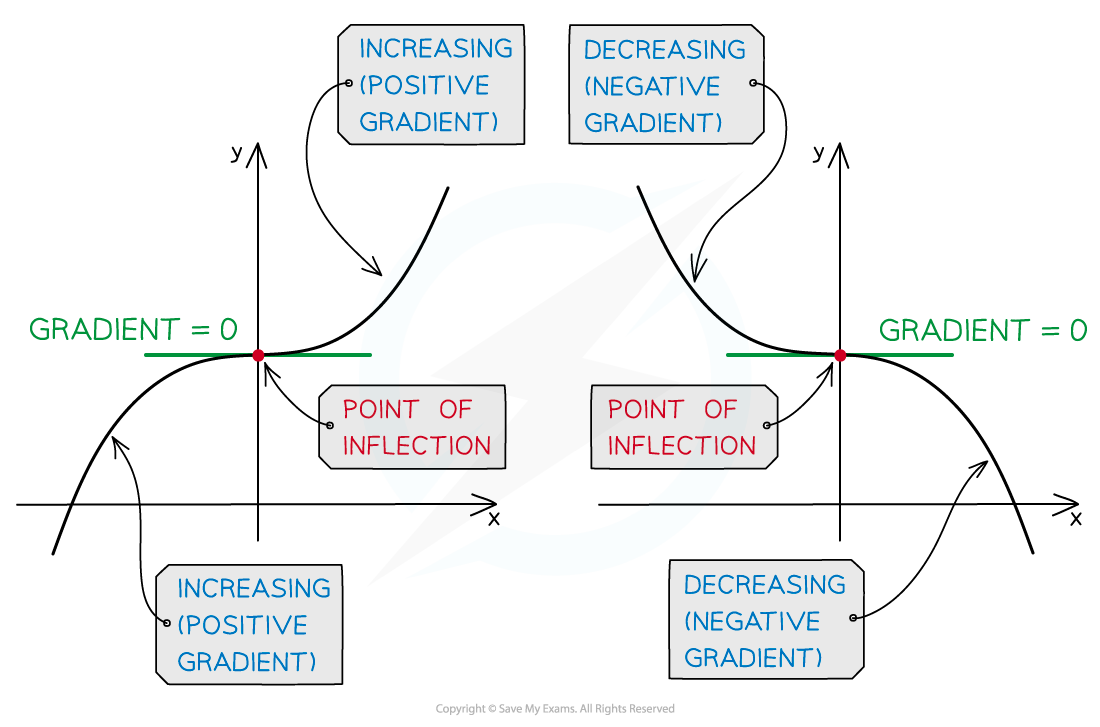
If the signs of the derivatives are the same on both sides (both positive or both negative) then the point is a point of inflection (a $_{/} -^{/}$ shape)

incr decr min max, A Level & AS Maths: Pure revision notes

Stationary Points point of inflection, A Level & AS Maths: Pure revision notes

Method B
- Look at the sign of the second derivative (positive or negative) at the stationary point
- (After completing Steps 1 - 3 above to find the stationary points)

Step 4
Find the second derivative $\frac{d^{2} y}{d x^{2}}$

Step 5
For each stationary point find the value of $\frac{d^{2} y}{d x^{2}}$ at the stationary point
i.e. substitute the x-coordinate of the stationary point into $\frac{d^{2} y}{d x^{2}}$ and evaluate

If $\frac{d^{2} y}{d x^{2}}$ is positive then the point is a local minimum
If $\frac{d^{2} y}{d x^{2}}$ is negative then the point is a local maximum
If $\frac{d^{2} y}{d x^{2}}$ is zero then the point could be a local minimum, a local maximum OR a point of inflection
- use Method A to determine which

Examiner Tips and Tricks

Usually, using the second derivative (Method B above) is a much quicker way of determining the nature of a stationary point.
- However, if the second derivative is zero it tells you nothing about the point
  - In this case you will have to use Method A
  - This method always works – see the Worked Example

Worked Example

Find the stationary points of

$y = x^{3} (3 x^{2} - 20)$

and determine the nature of each.

Start by expanding the brackets in the expression for $y$

$y = 3 x^{5} - 20 x^{3}$

Step 1
Find the first derivative

$\frac{d y}{d x} = 15 x^{4} - 60 x^{2}$

Step 2
Solve $\frac{d y}{d x} = 0$

$\begin{array}{rcl} 15 x^{4} - 60 x^{2} & = & 0 \end{array}$

Divide through by 15

$\begin{array}{rcl} x^{4} - 4 x^{2} & = & 0 \end{array}$

Fully factorise, spotting the difference of two squares

$\begin{array}{rcl} x^{4} - 4 x^{2} & = & 0 \\ x^{2} (x^{2} - 4) & = & 0 \end{array}$

Solve to find the $x$ -coordinates of the stationary (turning) points

$x = 0, - 2, 2$

Step 3
Find the corresponding $y$ -coordinates

$\begin{array}{rcl} x & = & 0, y = {(0)}^{3} (3 {(0)}^{2} - 20) = 0 \\ x & = & - 2, y = {(- 2)}^{3} (3 {(- 2)}^{2} - 20) = 64 \\ x & = & 2, y = {(2)}^{3} (3 {(2)}^{2} - 20) = - 64 \end{array}$

Write the answers as coordinates, being careful to correctly match $x$ 's and $y$ 's

The stationary points are (0, 0), (-2, 64) and (2, -64)

To find the nature of each stationary point, start with Method B
Step 4
Find the second derivative

$\frac{d^{2} y}{d x^{2}} = 60 x^{3} - 120 x$

Step 5
Evaluate the second derivative at each stationary point

$\begin{array}{rcl} x & = & 0, \frac{d^{2} y}{d x^{2}} = 60 {(0)}^{3} - 120 (0) \end{array}$ = 0

$\begin{array}{rcl} x & = & - 2, \frac{d^{2} y}{d x^{2}} = 60 {(- 2)}^{3} - 120 (- 2) = - 240 \end{array}$ < 0

$\begin{array}{rcl} x & = & 2, \frac{d^{2} y}{d x^{2}} = 60 {(2)}^{3} - 120 (2) = 240 \end{array}$ > 0

The nature of two of the stationary points is now determined

(-2, 64) is a local maximum point
(2, -64) is a local minimum point

For the third stationary point, (0, 0) switch to Method A
Step 4
Compare first derivatives a little to the left and right of $x = 0$

Choose $x = - 1$ and $x = 1$

$x = - 1, \frac{d y}{d x} = 15 {(- 1)}^{4} - 60 {(- 1)}^{2} = - 45$ < 0

$x = 1, \frac{d y}{d x} = 15 {(1)}^{4} - 60 {(1)}^{2} = - 45$ < 0

Step 5
Interpret the result and state the answer

$\frac{d y}{d x}$ has the same sign on both sides of (0, 0)

(0, 0) is a point of inflection

Last updated: 5 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: