Revision NotesExam QuestionsPast Papers
GCSEFurther MathsAQARevision Notes4. CalculusApplications of DifferentiationIncreasing & Decreasing Functions

Increasing & Decreasing Functions (AQA GCSE Further Maths)

Revision Note

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

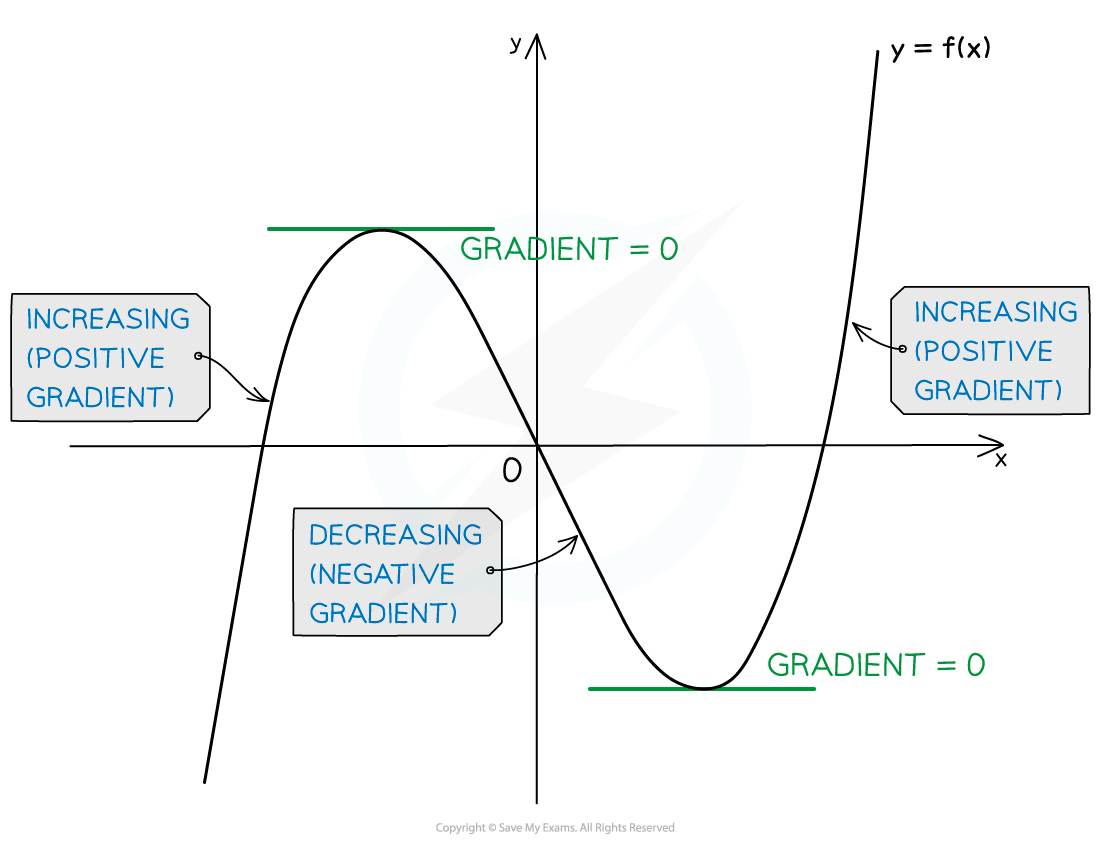
Increasing & Decreasing Functions

What are increasing and decreasing functions?

  • A function is increasing when fraction numerator d y over denominator d x end fraction greater than 0 (the gradient is positive)

    • This means graph of a function goes up as bold italic x increases

  • A function is decreasing when fraction numerator d y over denominator d x end fraction less than 0 (the gradient is negative)

    • This means graph of a function goes down as bold italic x increases 

Incr Decr Illustr 1, A Level & AS Maths: Pure revision notes

  • To identify the intervals (the range of x values) for which a curve is increasing or decreasing you need to:

  1. Find the derivative fraction numerator d y over denominator d x end fraction

  2. Solve the inequalities fraction numerator d y over denominator d x end fraction greater than 0 (for increasing intervals) or fraction numerator d y over denominator d x end fraction less than 0 (for decreasing intervals)

Examiner Tips and Tricks

  • In an exam, if you need to show a function is increasing or decreasing you can use either strict (<, >) or non-strict (≤, ≥) inequalities

    • You will get the marks either way in this course

Worked Example

For what values of x is y equals 2 x cubed minus 3 x squared plus 5 a decreasing function?

The function is decreasing when its gradient open parentheses fraction numerator d y over denominator d x end fraction close parentheses is less than 0.

Find the derivative of the function by differentiating.

table attributes columnalign right center left columnspacing 0px end attributes row cell fraction numerator d y over denominator d x end fraction end cell equals cell space 6 x squared space minus space 6 x end cell end table 

Solve the inequality fraction numerator d y over denominator d x end fraction space less than space 0 to find the set of values where the gradient is negative.

table row cell 6 x squared space minus space 6 x space end cell less than cell space 0 end cell end table

Factorise.

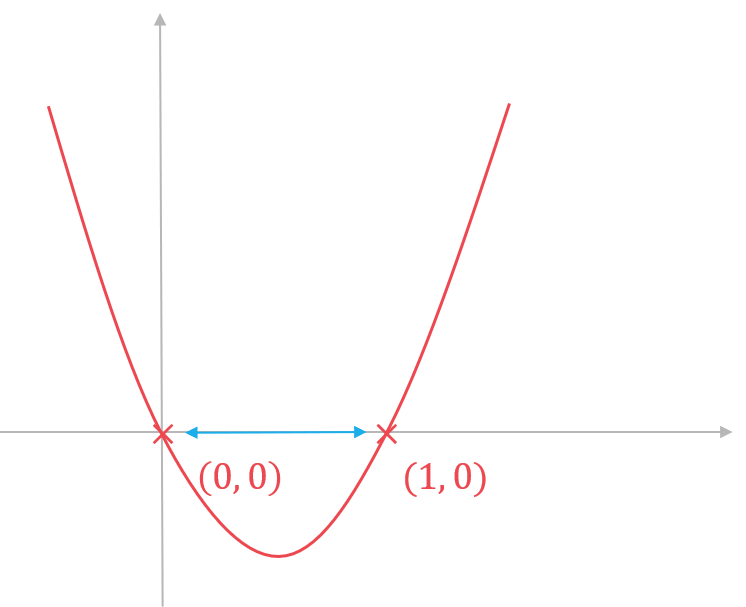
table row cell 6 x open parentheses x space minus space 1 close parentheses space end cell less than cell space 0 end cell end table

The solutions to fraction numerator d y over denominator d x end fraction space equals space 0 are x space equals space 0 and  x space equals space 1. Find the correct way around for the inequalities by considering the graph of fraction numerator d y over denominator d x end fraction. The graph is a positive quadratic, so the function is negative between the values of 0 and 1 (where it is below the x-axis).

Considering a sketch of the graph of the gradient function may help you see this.

3CqZzydq_aqa-fm-increasing-and-decreasing-functions-rn-diagram-we-1

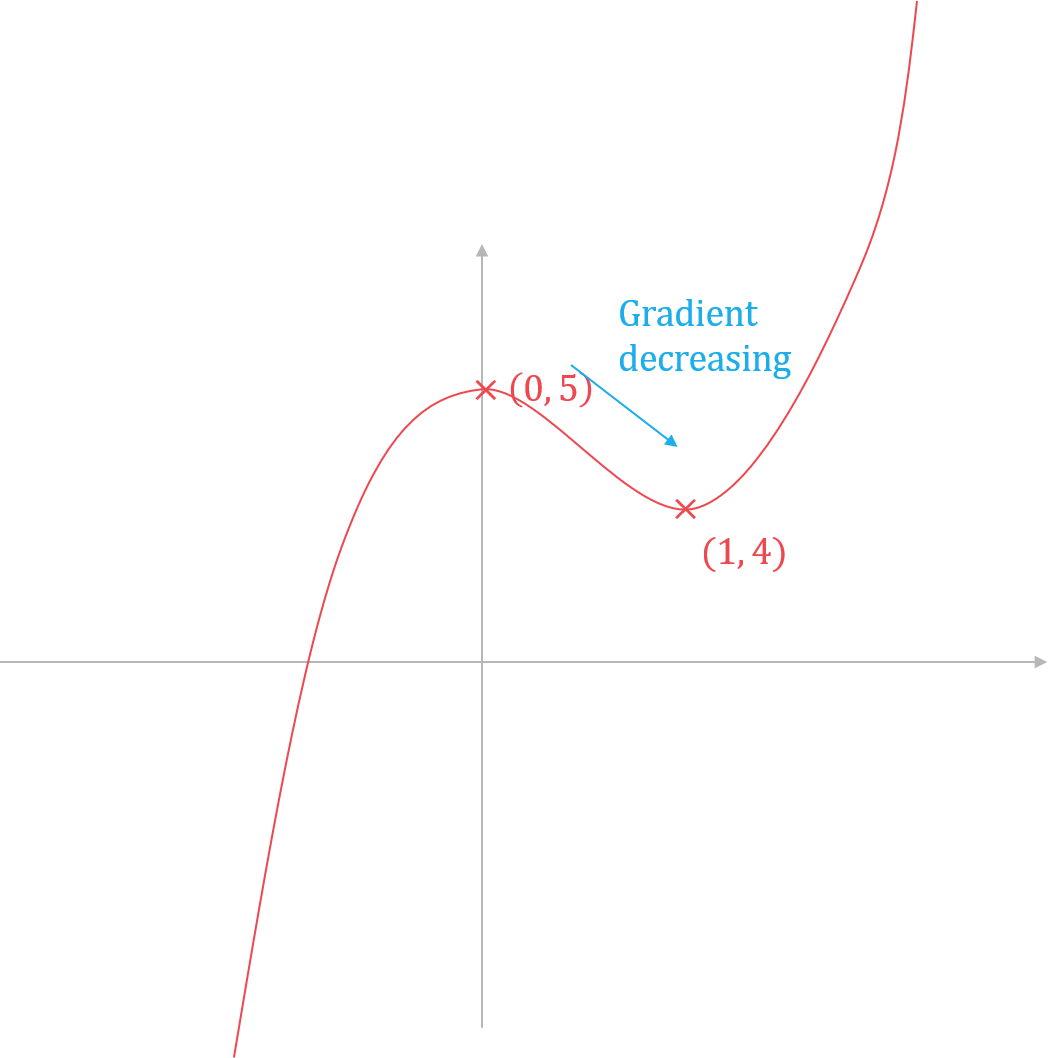
 You can check your answers by considering a sketch of the original function, it should be decreasing at the point where 0 space less than space x space less than space 1.

aqa-fm-increasing-and-decreasing-functions-rn-diagram-we-2

bold 0 bold space bold less than bold space bold italic x bold space bold less than bold space bold 1

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Tangents & NormalsNext:Second Derivatives
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.