Tangents to Circles (AQA GCSE Further Maths): Revision Note

Tangents to Circles

What is a tangent to a circle?

• A tangent is a line that touches a circle at a single point but doesn't cut across the circle

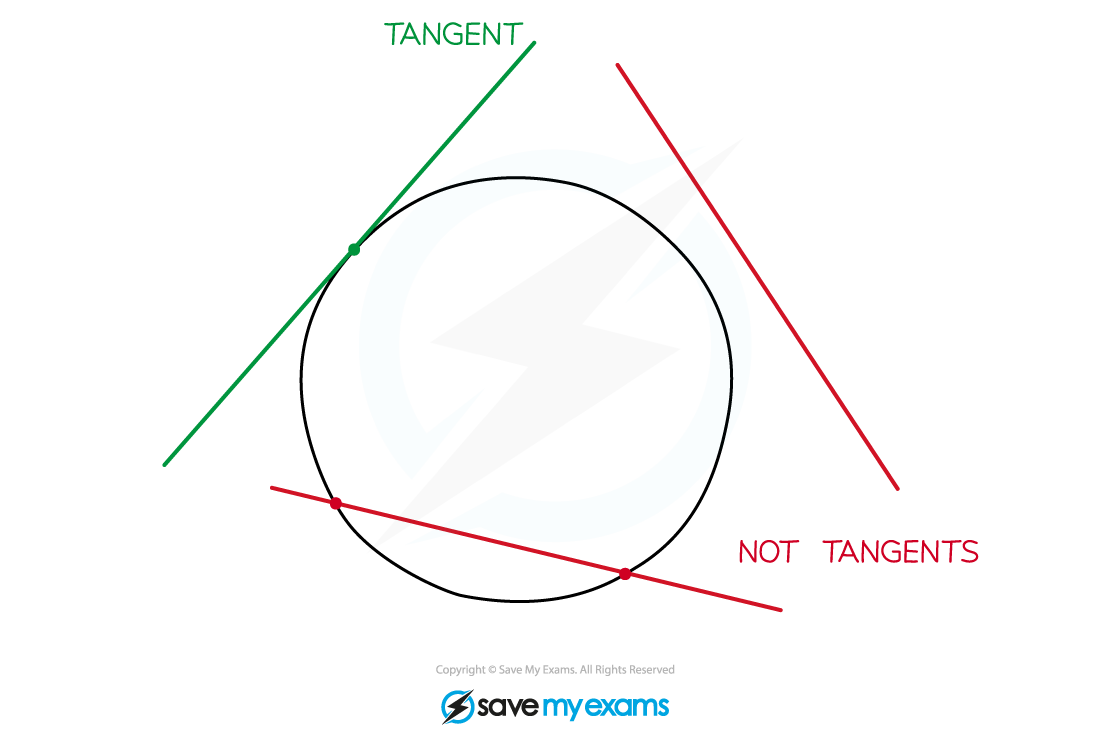
How is a tangent to a circle related to the radius?

• A tangent to a circle is perpendicular to the radius of the circle at the point of intersection

How can I find the equation of the tangent line to a circle at a given point?

•  STEP 1: Find the gradient of the radius OP 

• STEP 2: Find the gradient of the tangent

• STEP 3: We'll now know a point on the (tangent) line (x₂, y₂) and it's gradient, m, say

  • Substituting these into  allows us to find c

    • i.e.  

  • Then we can write down the equation of the tangent in the form

  • You could alternatively use the form  for the equation of the line