Gradients (AQA GCSE Further Maths): Revision Note
Exam code: 8365
Did this video help you?
Gradients of lines
What is the gradient of a line?
The gradient is a measure of how steep a 2D line is
A large value for the gradient means the line is steeper than for a small value of the gradient
A gradient of 3 is steeper than a gradient of 2
A gradient of −5 is steeper than a gradient of −4
A positive gradient means the line goes upwards from left to right - "uphill"
A negative gradient means the line goes downwards from left to right - "downhill"
In the equation for a straight line,
, the gradient is represented by
The gradient of
is −3
How do I find the gradient of a line?
The gradient can be calculated using
You may see this written as
instead
may even be used which links to the work on Calculus
this can be read as "the difference in y divided by the difference in x"
You need to know two coordinates a line passes through to find its gradient
If given two coordinates
and
the gradient of the line joining them is
The order of the coordinates must be consistent on the numerator and denominator
i.e. ("Point 2" – "Point 1") or ("Point 1" – "Point 2") for both
If given a diagram of a straight line you will need to pick two points the line passes through
If possible, pick whole number coordinates
positive numbers are easier to work with than negatives!
try not to pick coordinates that are close together
Examiner Tips and Tricks
Be very careful with negative numbers when calculating the gradient; write down your working rather than trying to do it in your head to avoid mistakes
For example,
Worked Example
a)
Find the gradient of the line joining (-1, 4) and (7, 28)
Using :
Simplify:
Gradient = 3
b)
Work out the gradient of the line shown in the diagram below.
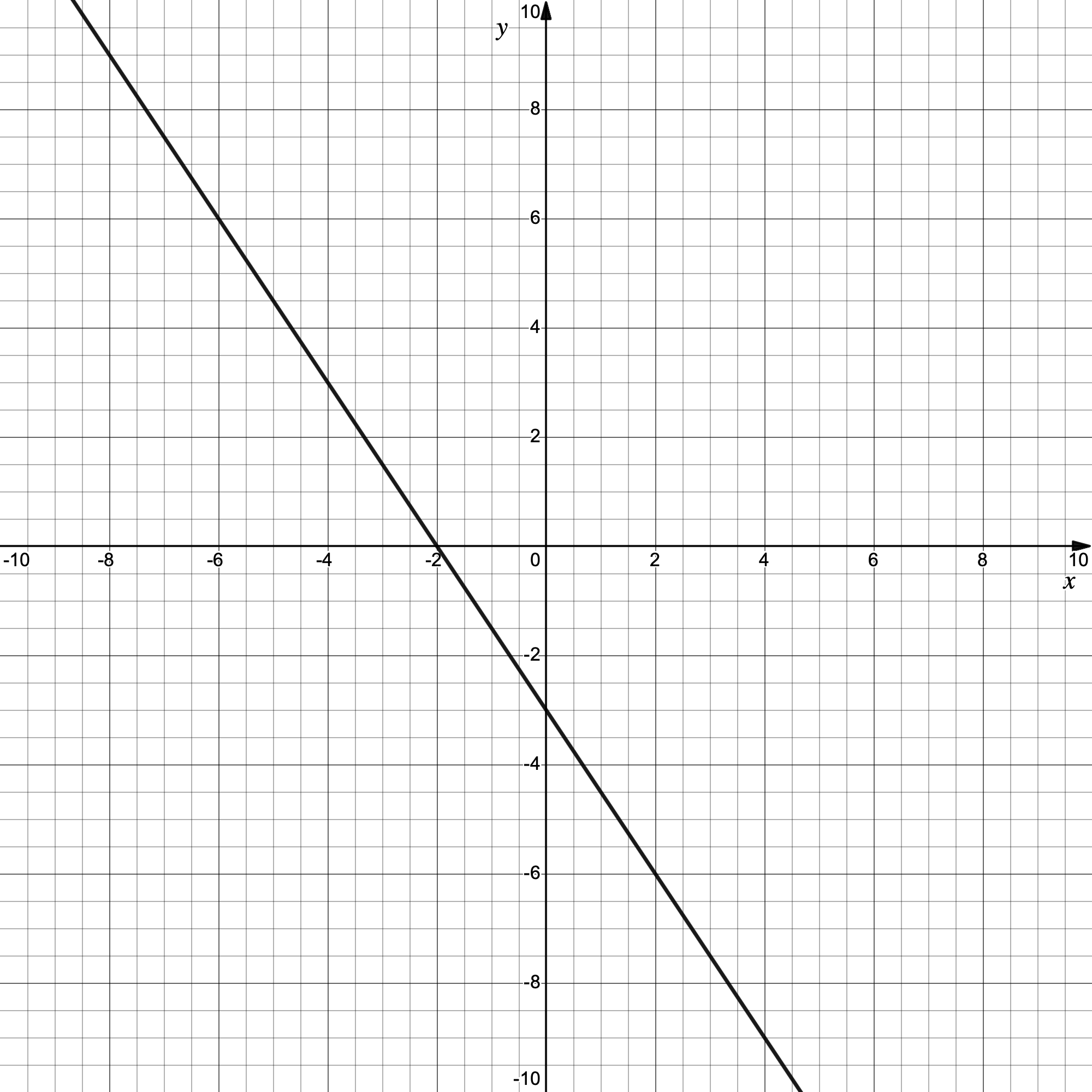
First note that this is a "downhill" line so we are expecting a negative gradient
We first need to identify two points on the line - looking for whole numbers we can see that the line passes through (-2, 0) and (2, -6)
Using
Simplify
Gradient
Parallel & perpendicular gradients
What are parallel lines?

Parallel lines are equidistant meaning they never meet
Parallel lines have equal gradients

What are perpendicular lines?

Perpendicular lines meet at right angles
The product of their gradients is -1

How do I tell if lines are parallel or perpendicular?
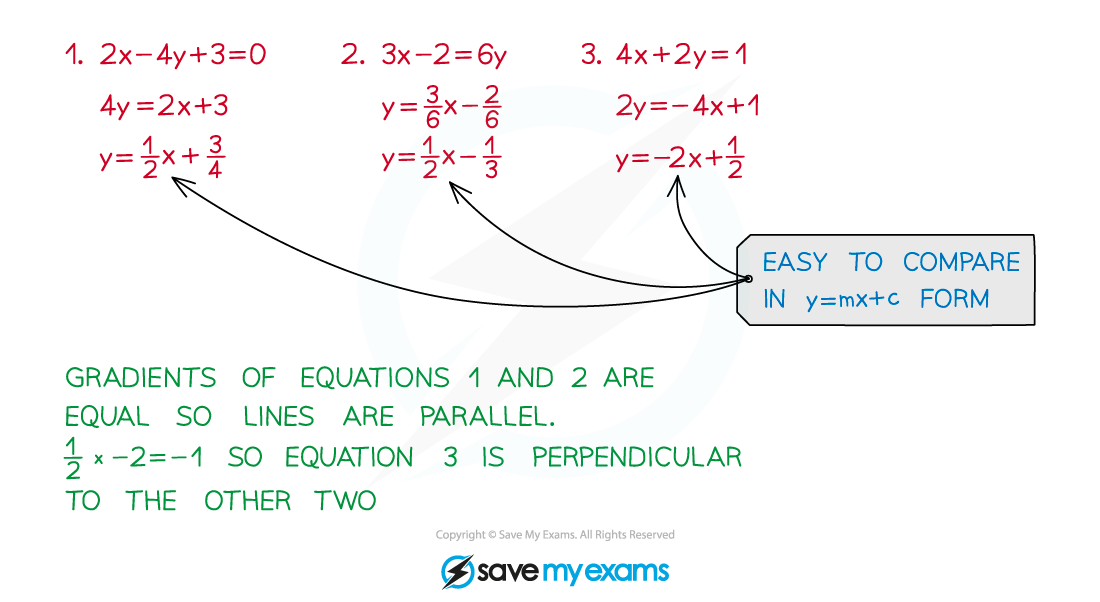
Rearrange equations into the form y = mx + c
m is the gradient
Examiner Tips and Tricks
Exam questions are good at “hiding” parallel and perpendicular lines.
e.g. a tangent and a radius are perpendicular
typically this would be shown using a diagram
Parallel lines could be implied by phrases like “… at the same rate …”
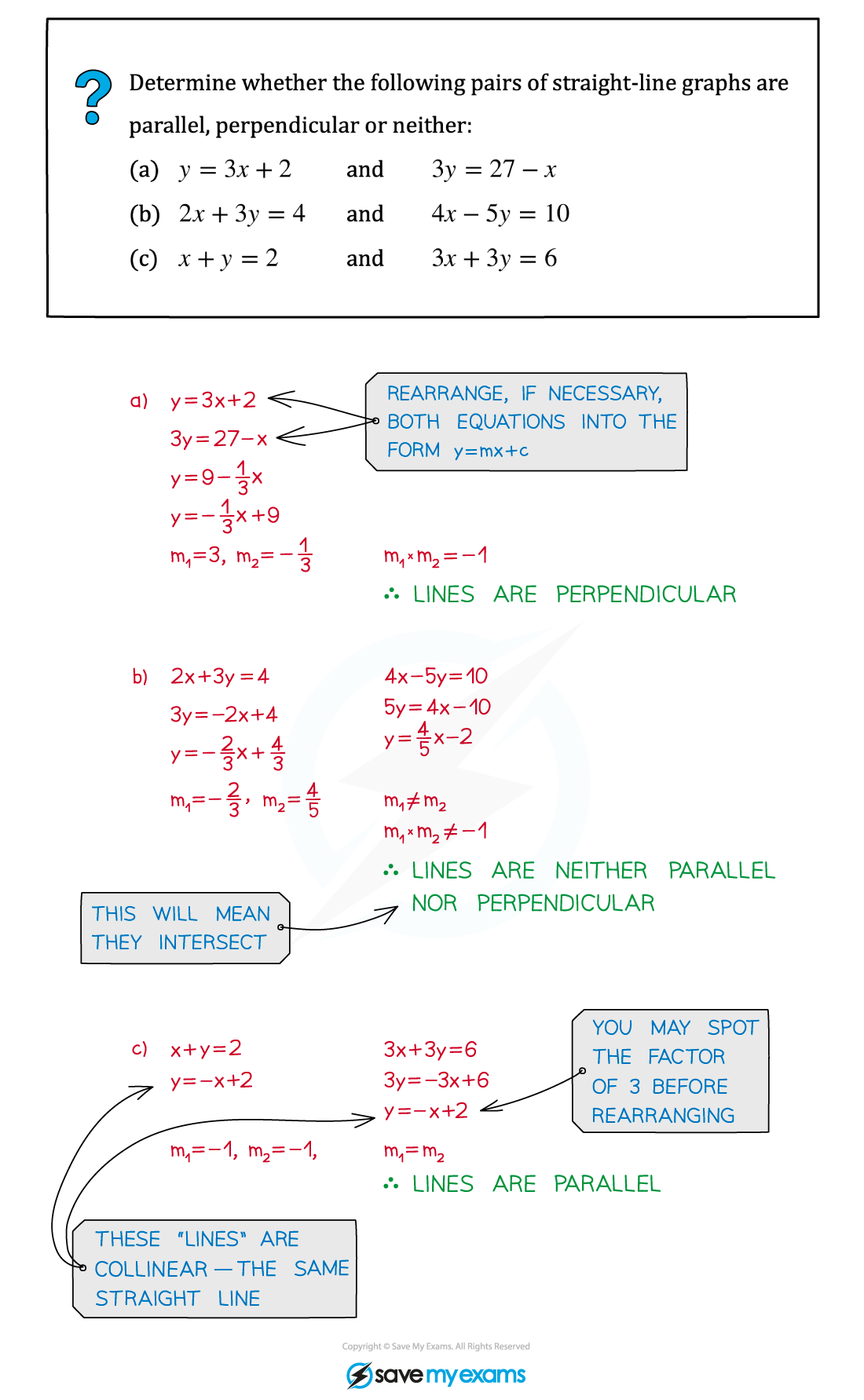
Worked Example

Unlock more, it's free!
Did this page help you?