Equation of a Straight Line (AQA GCSE Further Maths)

Revision Note

Test yourself

Written by: Jamie Wood

Reviewed by: Dan Finlay

Equation of a Straight Line

What is the equation of a straight line?

y = mx + c is the equation for any straight line
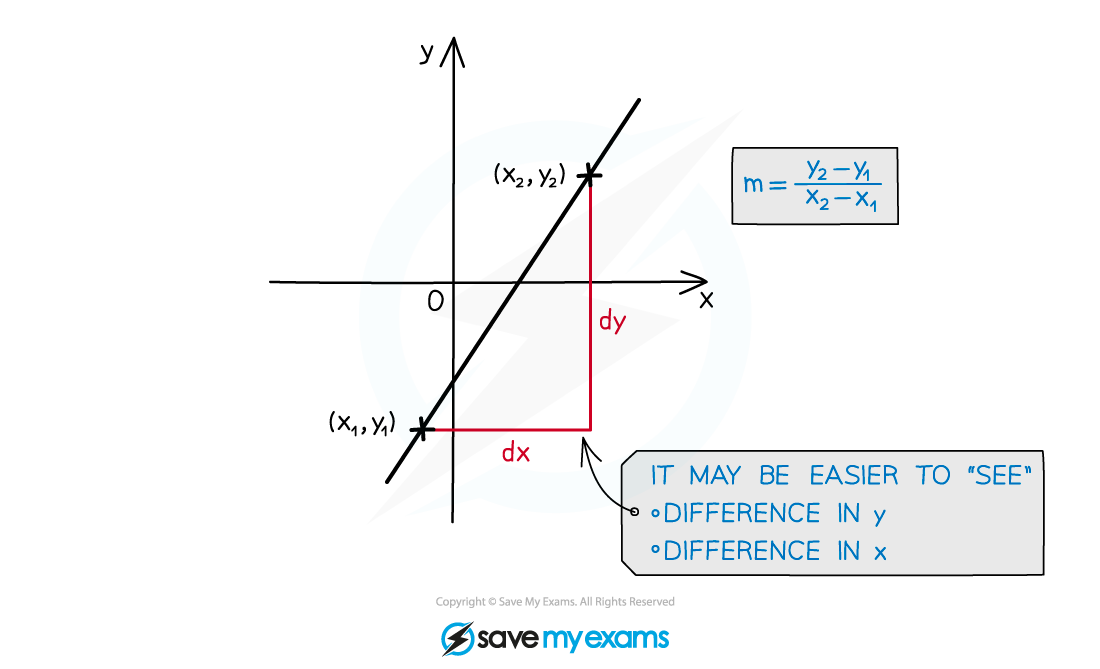
m is gradient given by “difference in y” ÷ “difference in x” or $\frac{d y}{d x}$
c is the y-axis intercept
An alternative form is ax + by + c = 0
- where a, b and c are integers

Equation of a Straight Line Notes Diagram 1, A Level & AS Level Pure Maths Revision Notes

How do I find the equation of a straight line?

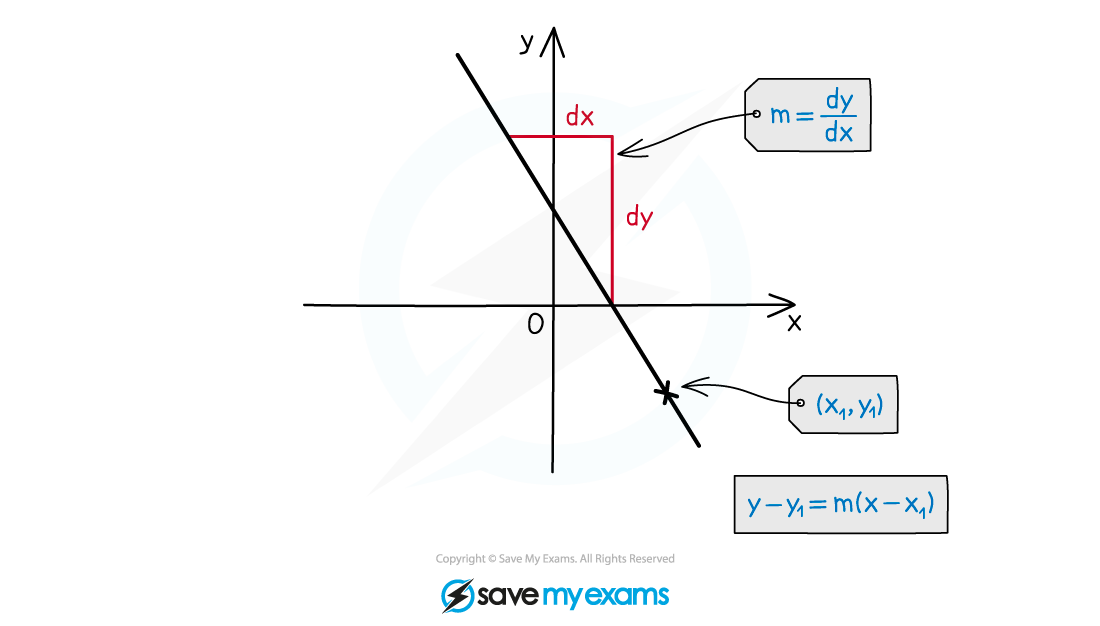
Equation of a Straight Line Notes Diagram 2, A Level & AS Level Pure Maths Revision Notes

Two features of a straight line are needed
- gradient, m
- a point the line passes through, (x₁, y₁)

The equation can then be found using y – y₁ = m(x - x₁)
This can be arranged into either y = mx + c or ax + by + c = 0

Equation of a Straight Line Notes Diagram 6, A Level & AS Level Pure Maths Revision Notes

How do I find the gradient of a straight line?

There are lots of ways to find the gradient of a line

Using two points on a line to find the change in y divided by change in x

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

Equation of a Straight Line Notes Diagram 3, A Level & AS Level Pure Maths Revision Notes

Using the fact that lines are parallel or perpendicular to another line
- see Gradients - Parallel and Perpendicular Gradients

Equation of a Straight Line Notes Diagram 4, A Level & AS Level Pure Maths Revision Notes

Using Tangents and Normals - Differentiation
- see Tangents & Normals

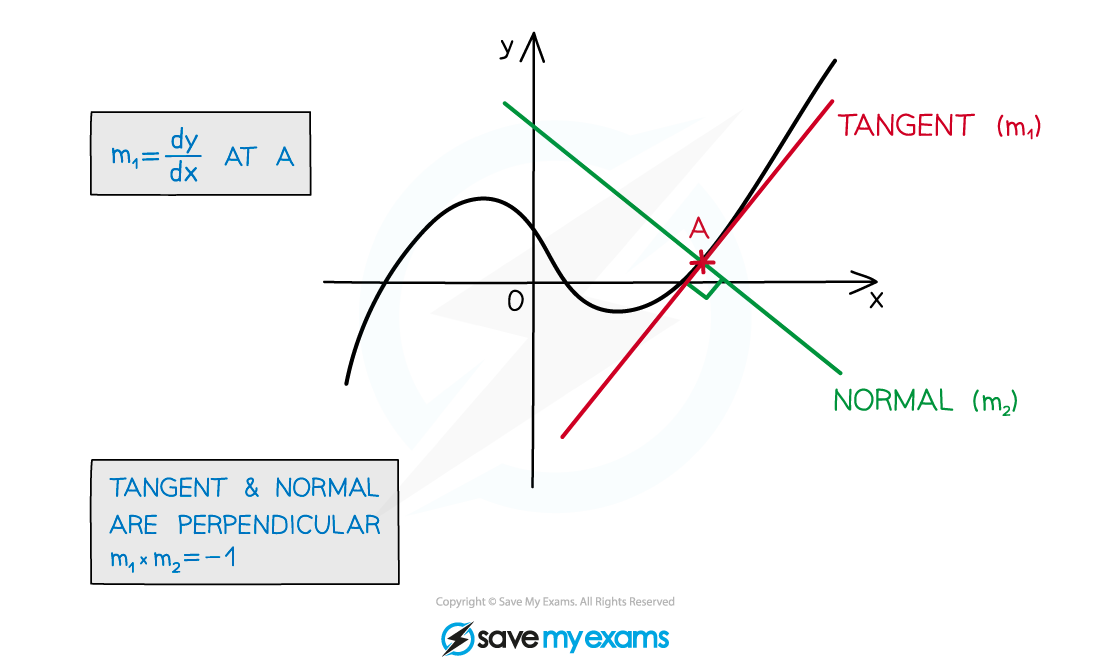
Equation of a Straight Line Notes Diagram 5, A Level & AS Level Pure Maths Revision Notes

Other ways
- Collinear lines are the same straight line so gradients are equal
- Angle facts and circle theorems
  e.g. a radius and tangent are perpendicular

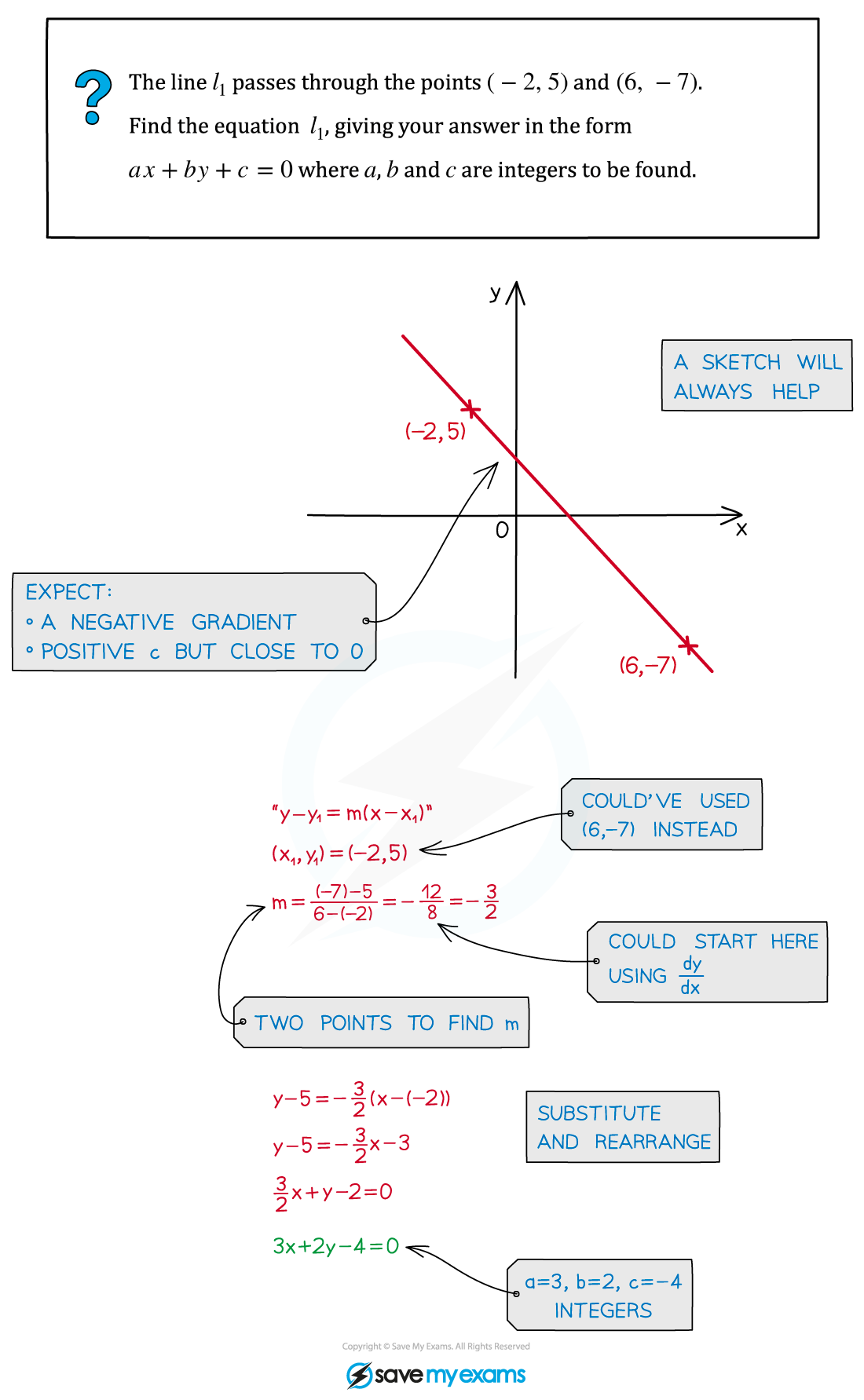
Worked Example

Equation of a Straight Line Example Diagram, A Level & AS Level Pure Maths Revision Notes

Intersection of Two Lines

How do I find where two lines intersect?

The coordinates of the point of intersection of two lines, $(x, y)$ , is the solution for $x$ and $y$ when the pair of equations are solved simultaneously
- A pair of parallel lines will not have any intersections, and therefore no solutions to the simultaneous equation, so it is useful to check if the lines are parallel before trying to solve them
We can find the solutions using either substitution or elimination
The most straight-forward method for finding where two straight lines intersect is to
- Rearrange each line's equation to $y = . . .$
- Substitute one expression for $y$ into the other equation, in place of $y$
- Solve to find $x$
- Substitute the value of $x$ into either line's equation to find $y$
The method is exactly the same when finding where a line and a curve, or two curves, intersect
- When finding where a quadratic curve and a line intersect, you will end up with a quadratic equation to solve, and there could be either 2, 1, or 0 solutions
  - This corresponds to the number of intersections of the line and the curve
The same idea can be used to find the intersection of a line or curve with the $x$ or $y$ axis
- The equation of the $y$ -axis is $x = 0$
- The equation of the $x$ -axis is $y = 0$
- Either of these can be substituted into the equation of the line or curve and solved

Solving Equations Graphically Notes Diagram 1, A Level & AS Level Pure Maths Revision Notes

Solving Equations Graphically Notes Diagram 2, A Level & AS Level Pure Maths Revision Notes

Examiner Tips and Tricks

Consider the types of graphs (straight line, quadratic, cubic) that you are finding the intersections of
Sketch a graph to help you consider the number of intersections there will be, and roughly where those will be

Worked Example

Find the points of intersection of the following

(a) $2 x + 3 y = 24$ with the $x$ -axis and $y$ -axis

The equation of the $x$ -axis is $y = 0$
Substitute this in to the other (given) equation

$2 x + 3 (0) = 24$

Solve for $x$

$\begin{array}{rcl} 2 x & = & 24 \\ x & = & 12 \end{array}$

There is no need to solve for $y$ , since $y = 0$

The point of intersection with the x-axis is (12, 0)

The equation of the $y$ -axis is $x = 0$
Substitute this in to the other (given) equation

$2 (0) + 3 y = 24$

Solve for $y$

$\begin{array}{rcl} 3 y & = & 24 \\ y & = & 8 \end{array}$

There is no need to solve for $x$ , since $x = 0$

The point of intersection with the y-axis is (0, 8)

(b) $y = 2 x - 1$ and $4 x + y = 26$

These are the equations of two straight lines
The easiest way to find their intersection is to start by writing both in the form $y = . . .$
The first equation already is but the second equation becomes

$y = 26 - 4 x$

Substitute this for $y$ in the first equation and solve for $x$

$\begin{array}{rcl} 26 - 4 x & = & 2 x - 1 \\ 26 + 1 & = & 2 x + 4 x \\ 6 x & = & 27 \\ x & = & 4.5 \end{array}$

Substitute this value of $x$ into either of the original equations and solve for $y$

$\begin{array}{rcl} y & = & 2 (4.5) - 1 \\ y & = & 8 \end{array}$

The point of intersection between the two lines is (4.5, 8)

One of these equations is quadratic (and already in the form $y = . . .$ )
The second (straight line) equation needs rearranging to $y = . . .$ form

$y = 3 x - 7$

Substitute this for $y$ into the first equation and rearrange to a quadratic equation

$\begin{array}{rcl} 3 x - 7 & = & x^{2} - 5 x + 5 \\ x^{2} - 5 x + 5 - 3 x + 7 & = & 0 \\ x^{2} - 8 x + 12 & = & 0 \end{array}$

Solve (if possible) this equation to find the $x$ -coordinates of any points of intersection
(Factorising, quadratic formula and completing the square are possible techniques or, if allowed, a calculator)

$\begin{array}{rcl} (x - 6) (x - 2) & = & 0 \\ x & = & 6 \\ x & = & 2 \end{array}$

Substitute these into either of the original equations to find the $y$ -coordinates
(Using the straight line equation is usually easiest)

$x = 6, y = 3 (6) - 7 = 11 x = 2, y = 3 (2) - 7 = - 1$

Write your final answers as coordinates but as there are two intersections be careful to match $x$ 's and $y$ 's correctly

The points of intersection between the curve and line are (6, 11) and (2, -1)

Finding Parallel & Perpendicular Lines

What are parallel lines?

Parallel lines are lines that have the same gradient, but are not the same line
Parallel lines do not intersect with each other
You can easily spot that two lines are parallel when they are written in the form $y = m x + c$ , as they will have the same value of $m$ (gradient)
- $y = 3 x + 7$ and $y = 3 x - 4$ are parallel
- $y = 2 x + 3$ and $y = 3 x + 3$ are not parallel
- $y = 4 x + 9$ and $y = 4 x + 9$ are not parallel; they are the exact same line

How do I find the equation of a line parallel to another line?

As parallel lines have the same gradient, a line of the form $y = m x + c$ will be parallel to a line in the form $y = m x + d$ , where $m$ is the same for both lines
- If $c = d$ then they would be the same line and therefore not parallel
If you are asked to find the equation of a line parallel to $y = m x + c$ , you will also be given some information about a point that the parallel line, $y = m x + d$ passes through; $(x_{1}, y_{1})$
You can then substitute this point into $y = m x + d$ and solve to find $d$

Did this video help you?

What are perpendicular lines?

You should already know that parallel lines have equal gradients
Perpendicular lines meet each other at right angles
- i.e. they meet at 90°

What’s the deal with perpendicular gradients (and lines)?

Before you start trying to work with perpendicular gradients and lines, make sure you understand how to find the equation of a straight line – that will help you do the sorts of questions you will meet
Gradients m₁ and m₂ are perpendicular if m₁ × m₂ = −1
- For example
  - 1 and -1
  - $\frac{1}{3}$ and -3
  - $- \frac{2}{3}$ and $\frac{3}{2}$
We can use m₂ = −1 ÷ m₁ to find a perpendicular gradient. This is called the negative reciprocal.
If in doubt, SKETCH IT!

Examiner Tips and Tricks

Working with straight lines can involve lots of algebra, but sketching a diagram will always help
Use a sketch to check if answers seem about right

Worked Example

(a)

Find the equation of the line that is parallel to $y = 3 x + 7$ and passes through (2,1).

As the gradient is the same, the line that is parallel will be in the form:

$y = 3 x + d$

Substitute in the coordinate that the line passes through:

$1 = 3 (2) + d$

Simplify:

$1 = 6 + d$

Subtract 6 from both sides:

$- 5 = d$

Final answer:

$y = 3 x - 5$

(b)

Find the equation of the line that is perpendicular to $y = 2 x - 2$ and passes through (2, -3).
Leave your answer in the form $a x + b y + c = 0$ where $a, b, c$ are integers.

L is in the form $y = m x + c$ so we can see that its gradient is 2

$m_{1} = 2$

Therefore the gradient of the line perpendicular to L will be the negative reciprocal of 2

$m_{2} = - \frac{1}{2}$

Now we need to find $c$ for the line we're after
Do this by substituting the point $(2, - 3)$ into the equation $y = - \frac{1}{2} x + c$ and solving for $c$

$\begin{array}{rcl} - 3 & = & - \frac{1}{2} \times 2 + c \\ - 3 & = & - 1 + c \\ c & = & - 2 \end{array}$

Now we know the line we want is

$\begin{array}{rcl} y & = & - \frac{1}{2} x - 2 \end{array}$

But this is not in the form asked for in the question. So rearrange into the form $a x + b y + c = 0$ where $a$ , $b$ and $c$ are integers

$\begin{array}{rcl} y + \frac{1}{2} x + 2 & = & 0 \\ 2 y + x + 4 & = & 0 \end{array}$

Write the final answer

$x + 2 y + 4 = 0$

Last updated: 5 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:GradientsNext:Equation of a Circle

Equation of a Straight Line (AQA GCSE Further Maths)

Revision Note

Equation of a Straight Line

What is the equation of a straight line?

How do I find the equation of a straight line?

How do I find the gradient of a straight line?

Worked Example

Intersection of Two Lines

How do I find where two lines intersect?

Examiner Tips and Tricks

Worked Example

Finding Parallel & Perpendicular Lines

What are parallel lines?

How do I find the equation of a line parallel to another line?

What are perpendicular lines?

What’s the deal with perpendicular gradients (and lines)?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Jamie Wood

Author: Dan Finlay