GCSEFurther MathsAQARevision Notes3. Coordinate GeometryCoordinate Geometry & Straight LinesCoordinate Geometry

Coordinate Geometry (AQA GCSE Further Maths)

Revision Note

Test yourself

Last updated

Distance Between Two Points

How do I calculate the distance between two points?

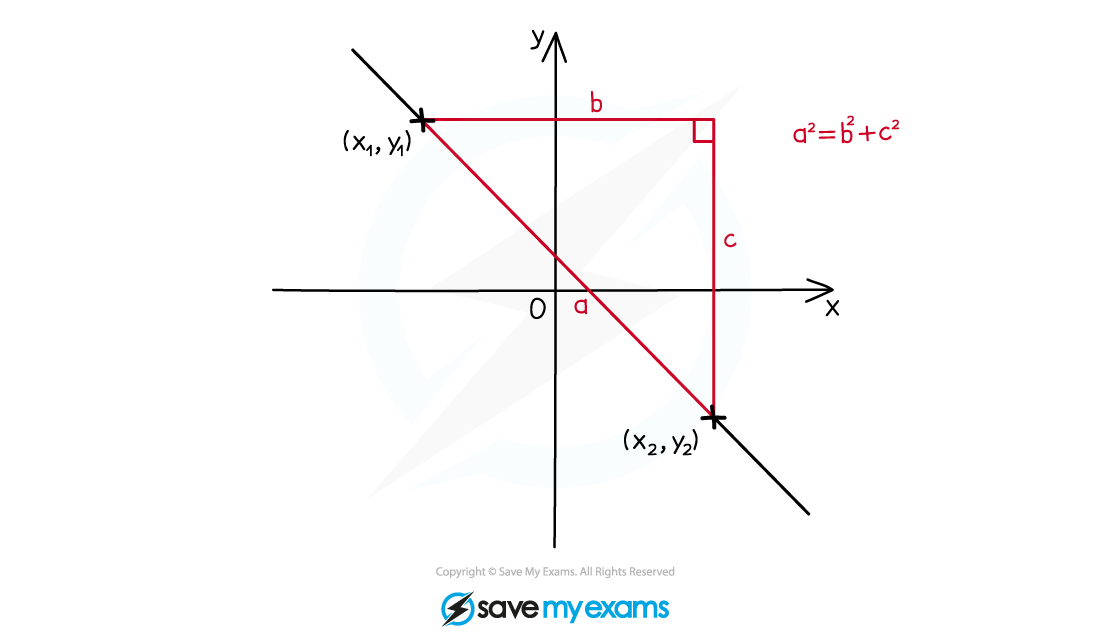
  • The distance between two points with coordinates open parentheses x subscript 1 space comma space y subscript 1 close parentheses and open parentheses x subscript 2 space comma space y subscript 2 close parentheses can be found using the formula

d equals square root of open parentheses x subscript 1 minus x subscript 2 close parentheses squared plus open parentheses y subscript 1 minus y subscript 2 close parentheses squared end root

  • This formula is really just Pythagoras’ Theorem  a squared equals b squared plus c squared, applied to the difference in the x-coordinates and the difference in the y-coordinates;

Basic Coordinate Geometry Notes Diagram 2

  • You may be asked to find the length of a diagonal in 3D space. This can be answered using 3D Pythagoras

Examiner Tips and Tricks

  • As we are squaring the difference in and  in the formula, it does not matter if they are positive or negative

    • 32 is the same as (-3)2, this may help to speed up your working

Worked Example

Point A has coordinates (3, -4) and point B has coordinates (-5, 2).

Calculate the distance of the line segment AB.

Using the formula for the distance between two points, d equals square root of open parentheses x subscript 1 minus x subscript 2 close parentheses squared plus open parentheses y subscript 1 minus y subscript 2 close parentheses squared end root 

Substituting in the two given coordinates:

d equals square root of open parentheses 3 minus negative 5 close parentheses squared plus open parentheses negative 4 minus 2 close parentheses squared end root

Simplify: 

d equals square root of open parentheses 8 close parentheses squared plus open parentheses negative 6 close parentheses squared end root space equals space square root of 64 plus 36 end root equals square root of 100 equals 10

Answer = 10 units

Midpoints

How do I find the midpoint of a line?

  • The midpoint of a line will be the same distance from both endpoints

  • You can think of a midpoint as being the average (mean) of two coordinates

  • The midpoint of open parentheses x subscript 1 comma space y subscript 1 close parentheses and open parentheses x subscript 2 comma space y subscript 2 close parentheses is

open parentheses fraction numerator x subscript 1 plus x subscript 2 over denominator 2 end fraction space comma space fraction numerator y subscript 1 plus y subscript 2 over denominator 2 end fraction close parentheses

Examiner Tips and Tricks

  • Unlike when finding the distance between two points, when finding a midpoint we are finding a location, so the negative signs definitely do matter here

    • Be very careful to include any negative signs, and check your calculations

Worked Example

The coordinates of A are (−4, 3) and the coordinates of B are (8, −12).

Find M, the midpoint of AB.

The midpoint can be found using M = open parentheses fraction numerator x subscript 1 plus x subscript 2 over denominator 2 end fraction space comma space fraction numerator y subscript 1 plus y subscript 2 over denominator 2 end fraction close parentheses

Fill in the values of x and y  from each coordinate

open parentheses fraction numerator negative 4 plus 8 over denominator 2 end fraction space comma space fraction numerator 3 plus negative 12 over denominator 2 end fraction close parentheses equals open parentheses 4 over 2 comma space fraction numerator negative 9 over denominator 2 end fraction close parentheses

Simplify

M = (2, −4.5)

Using a Ratio to Find a Point

How can I use a ratio to find a point on a line?

  • The midpoint of AB splits AB in the ratio 1 : 1.

  • If you are asked to find the point that divides AB in the ratio m : n, then you need to find the point that lies begin mathsize 16px style fraction numerator m over denominator m plus n end fraction end style of the way from A to B.

    • E.g. dividing AB in the ratio 2 : 3 means finding the point that is 2 over 5 of the way from A to B.

  • Normally an exam question will ask you to find the point that divides AB in the ratio 1 : n, so;

    • find the difference between the x coordinates,

    • divide this difference by [1 + n], and add the result to the x coordinate of A,

    • repeat for the y coordinates.

Worked Example

The coordinates of A are (−4, 3) and the coordinates of B are (8, −12).

A point N divides AB in the ratio 1 : 2.

Find the coordinates of N.

Calculate the difference between the x coordinate of A and the x coordinate of B

table row cell 8 minus open parentheses negative 4 close parentheses end cell equals 12 end table

Divide this difference by 3 (as there are 1 + 2 = 3 parts in the ratio 1 : 2)

table row cell 12 divided by 3 end cell equals 4 end table

Add 4 to the x coordinate of A

table row cell x space coordinate space of space N end cell equals cell negative 4 plus 4 equals 0 end cell end table

Repeat for y

table row cell negative 12 minus 3 end cell equals cell negative 15 end cell row cell open parentheses negative 15 close parentheses divided by 3 end cell equals cell negative 5 end cell row cell y space coordinate space of space N end cell equals cell 3 plus open parentheses negative 5 close parentheses equals negative 2 end cell end table

Alternatively, you may find it helpful to sketch the coordinates A and B and find N intuitively. Note that in the sketch, the coordinates do not need to be placed in the correct orientation to one another, simply along a straight line:

2-12-2-midpoints-we

Write the final answer as a coordinate point

N = (0, −2)

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Using nth Terms of SequencesNext:Gradients