Quadratic Inequalities (AQA GCSE Further Maths)

Revision Note

Test yourself

Written by: Mark Curtis

Reviewed by: Dan Finlay

Solving Quadratic Inequalities

What are quadratic inequalities?

A quadratic inequality has the form $a x^{2} + b x + c \geq 0$
- There is an $x^{2}$ term and any inequality sign, $\geq, \leq, >, <$
- They can usually be factorised
  - For example, $(x - 2) (x - 5) \geq 0$
Solutions to quadratic inequalities are ranges of $x$ values
- For example, $1 \leq x \leq 4$

How do I solve a quadratic inequality?

Quadratic inequalities are solved by sketching a graph
- The solutions then appears along the $x$ -axis
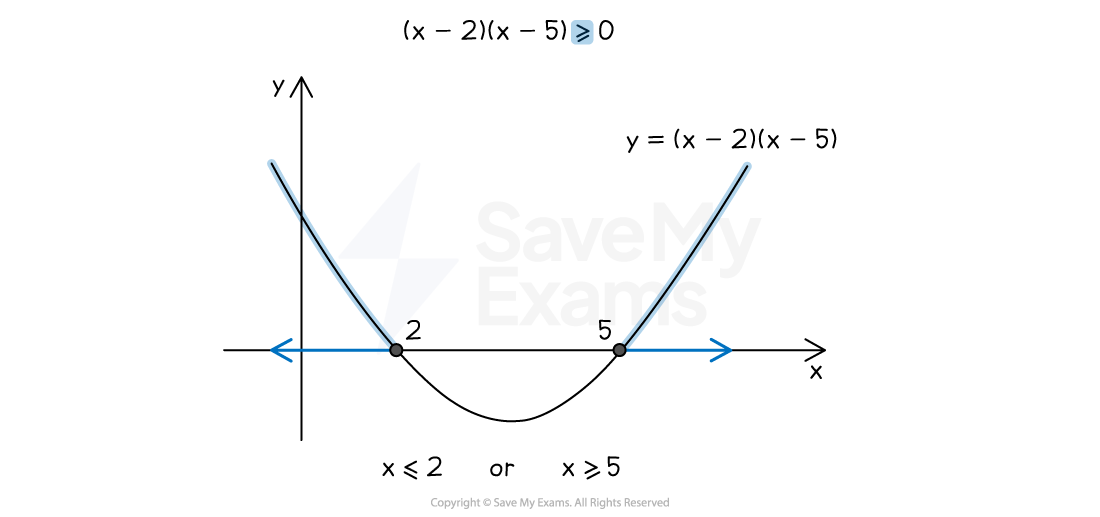
For example, to solve $(x - 2) (x - 5) \geq 0$
- Sketch the graph of $y = (x - 2) (x - 5)$
  - Show the $x$ -intercepts of 2 and 5
  - These come from solving $(x - 2) (x - 5) = 0$
- As the inequality is $\geq 0$ , shade any parts of the curve that are above the $x$ -axis
  - These are left of $x = 2$ and right of $x = 5$
- The solutions are the ranges on the $x$ -axis for those shaded parts
  - $x \leq 2$ or $x \geq 5$
  - Use the word "or" for two separate parts

Graph of quadratic inequality (x-2)(x-5) ≥ 0, showing shading for x ≤ 2 and x ≥ 5, and the quadratic function y = (x-2)(x-5) plotted, crossing x at 2 and 5.

What do I do if the sign of the inequality changes?

If the quadratic inequality is $a x^{2} + b x + c \geq 0$ where $a$ is positive
- then shade the parts of the curve above the $x$ -axis
If the quadratic inequality is $a x^{2} + b x + c \leq 0$ where $a$ is positive
- then shade the part of the curve below the $x$ -axis
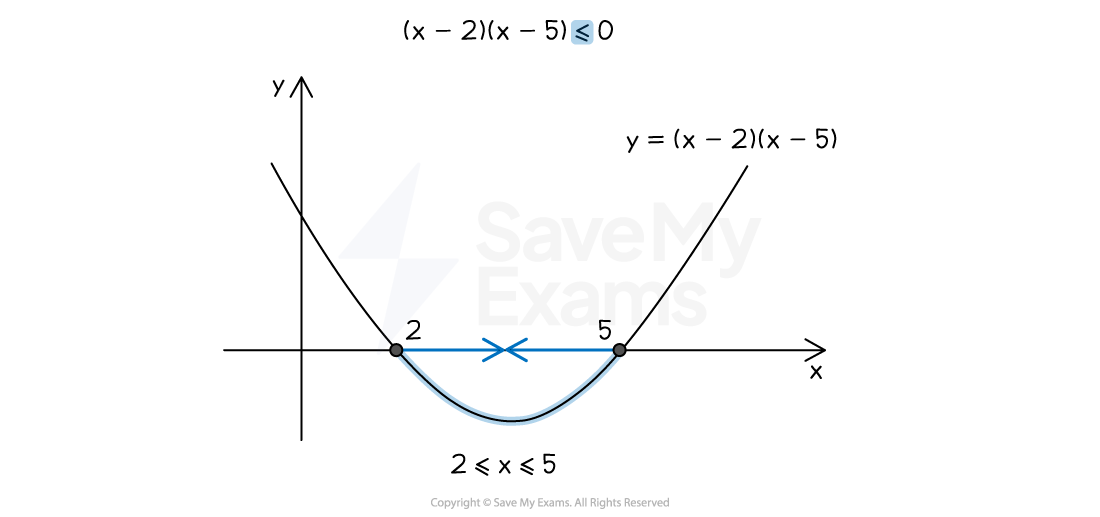
For example, to solve $(x - 2) (x - 5) \leq 0$
- Repeat the process above but shade where the curve is below the $x$ -axis
  - The solution is $2 \leq x \leq 5$
  - (You do not use the word "or", but could say $x \geq 2$ "and" $x \leq 5$ )

Graph depicting the quadratic inequality (x - 2)(x - 5) ≤ 0. The highlighted area shows y = (x - 2)(x - 5) between x = 2 and x = 5, inclusive.

If strict inequality signs are used, $>$ or $<$
- then you must use strict inequalities in your final answer

How can quadratic inequalities be made harder?

You may need to bring all the terms to one side first
- For example $x^{2} - x < 6$ becomes $x^{2} - x - 6 < 0$
  - It is easier to pick the side with a positive $x^{2}$
You may have to factorise the quadratic inequality first
- This may involve factorising
  - $a x^{2} + b x + c$ into double brackets
  - $a^{2} x^{2} - b^{2} = (a x + b) (a x - b)$ (the difference of two squares)
  - $a x^{2} + b x = x (a x + b)$ (factorising out an $x$ )
- If it does not factorise, you may need the quadratic formula to find $x$ -intercepts
You may be given a quadratic inequality $a x^{2} + b x + c \geq 0$ where $a$ is negative
- This means the sketch will be an $\cap$ shape
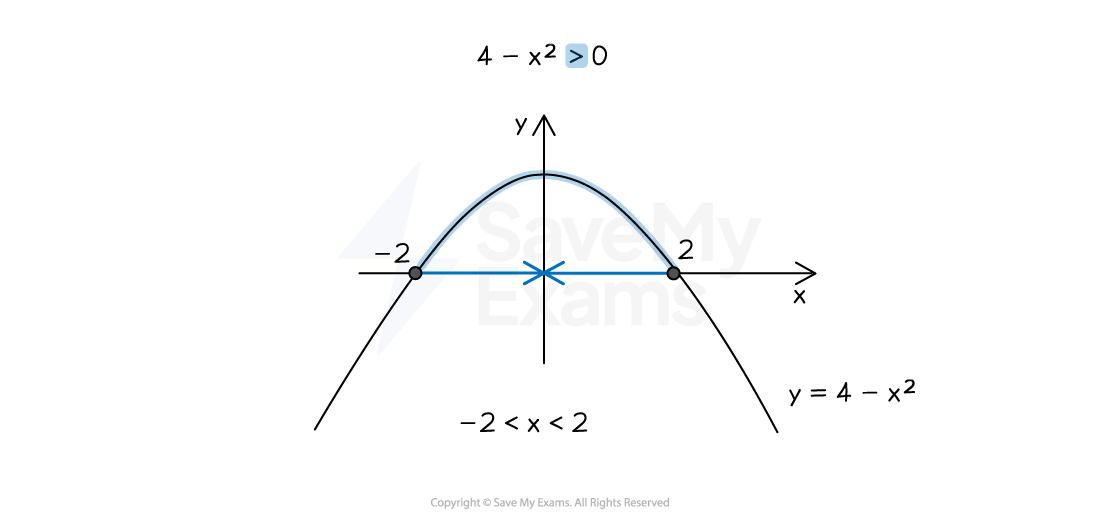
For example, solve $4 - x^{2} > 0$
- The $x$ intercepts are found from $4 - x^{2} = 0$ giving $x = \pm 2$
- The same process is then applied, but the graph has an $\cap$ shape

Graph of quadratic inequality 4 - x^2 > 0. The shaded region above y = 4 - x^2 shows valid x values between -2 and 2, excluding the endpoints.

Examiner Tips and Tricks

Think of inequalities with $x^{2}$ terms as graph-sketching questions in the exam.

Worked Example

Solve $2 x^{2} - 2 x + 5 > 9$ .

Bring all the terms to one side
It is easiest to use the left-hand side (giving a positive $x^{2}$ term)

$\begin{array}{rcl} 2 x^{2} - 2 x + 5 - 9 & > & 0 \\ 2 x^{2} - 2 x - 4 & > & 0 \end{array}$

Simplify the inequality by dividing both sides by 2

$\begin{array}{rcl} x^{2} - x - 2 & > & 0 \end{array}$

Factorise the quadratic expression on the left-hand side

$(x + 1) (x - 2) > 0$

Find the $x$ -intercepts of the graph $y = (x + 1) (x - 2)$
To do this, solve $(x + 1) (x - 2) = 0$

$(x + 1) (x - 2) = 0$ gives $x = - 1$ or $x = 2$

Sketch $y = (x + 1) (x - 2)$ (showing the $x$ -intercepts of -1 and 2)
The inequality is $. . . > 0$ so shade the parts of the curve above the $x$ -axis

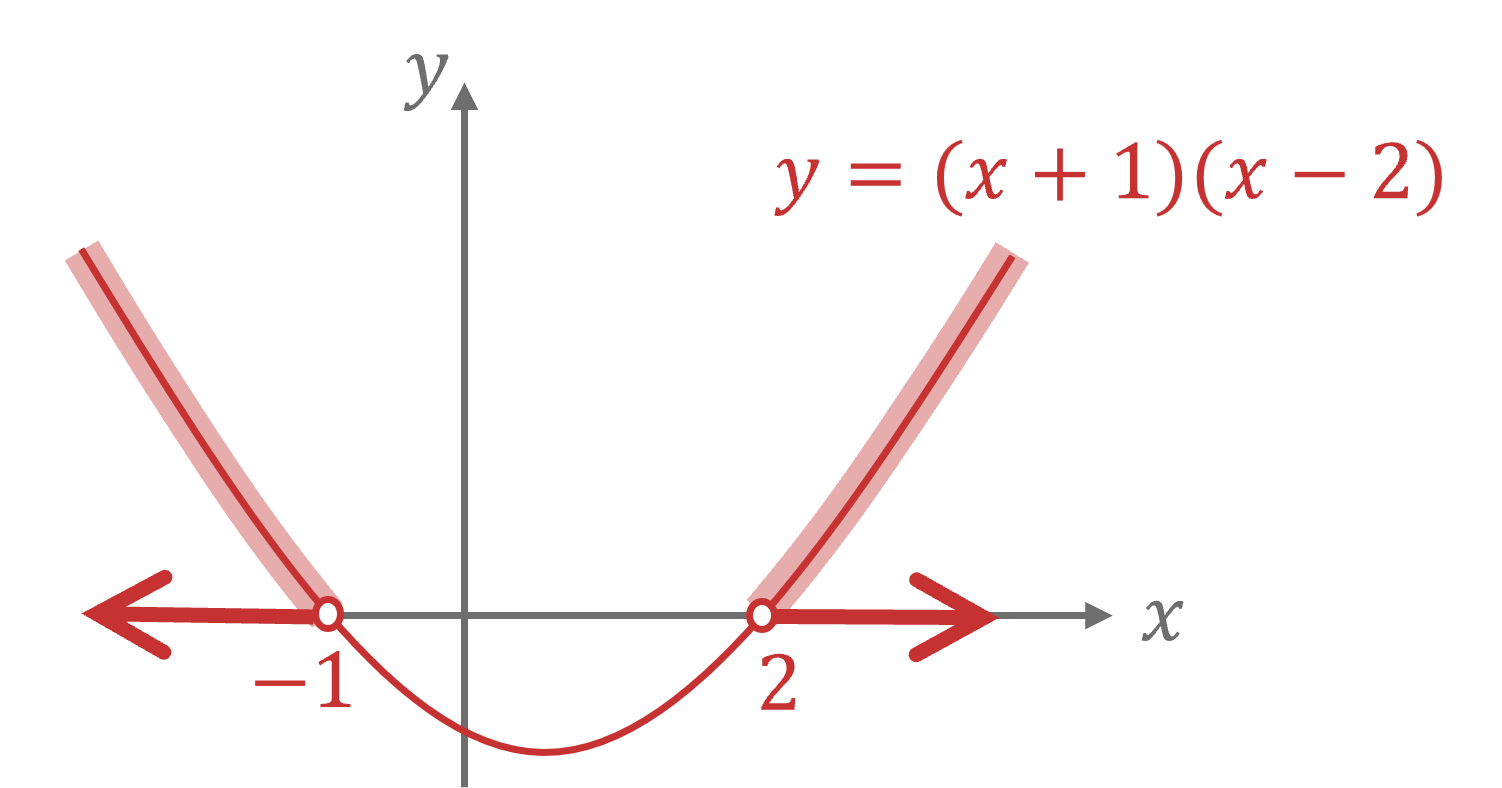
Graph of y = (x + 1)(x - 2) showing a parabola intersecting the x-axis at x = -1 and x = 2. The region shaded represents the quadratic inequality shown.

Write down the ranges on the $x$ -axis for the shaded parts above
Use the word "or" to separate the two solutions

$x < - 1$ or $x > 2$

Last updated: 11 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: