Quadratic & Polynomial Graphs (AQA GCSE Further Maths)

Revision Note

Written by: Jamie Wood

Reviewed by: Dan Finlay

Quadratic Graphs

A quadratic is a function of the form $y = a x^{2} + b x + c$ where $a$ is not zero
They are a very common type of function in mathematics, so it is important to know their key features

What does a quadratic graph look like?

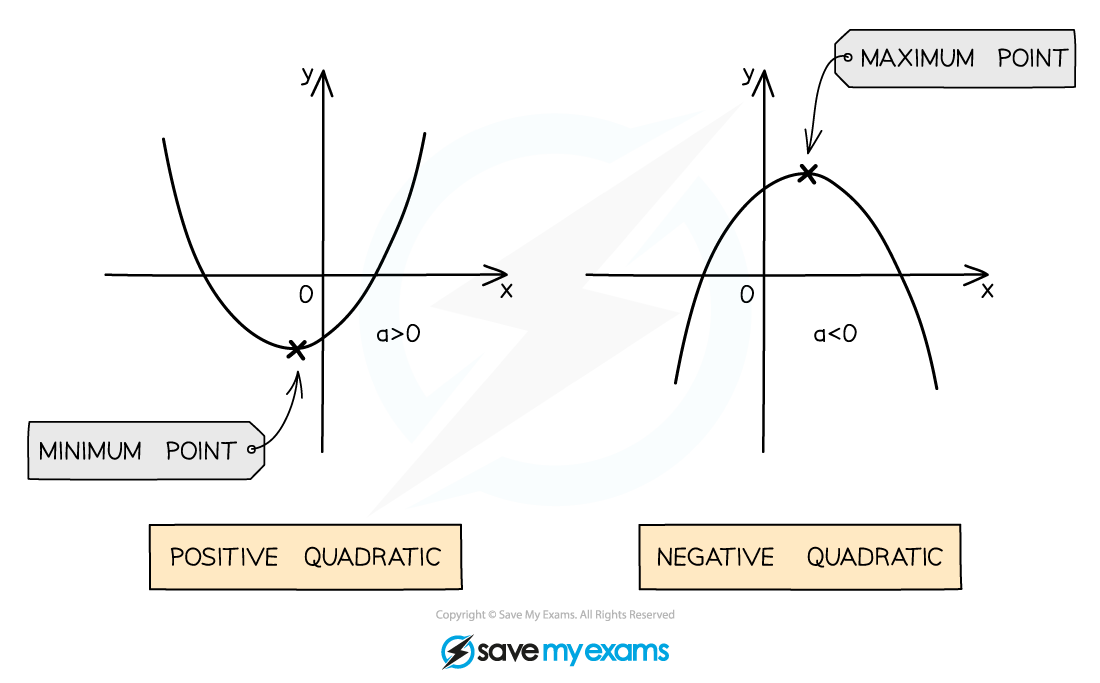
The shape made by a quadratic graph is known as a parabola
The parabola shape of a quadratic graph can either look like a “u-shape” or an “n-shape”
- A quadratic with a positive coefficient of $x^{2}$ will be a u-shape
- A quadratic with a negative coefficient of $x^{2}$ will be an n-shape
A quadratic will always cross the $y$ -axis
A quadratic may cross the $x$ -axis twice, once, or not at all
- The points where the graph crosses the $x$ -axis are called the roots
If the quadratic is a u-shape, it has a minimum point (the bottom of the u)
If the quadratic is an n-shape, it has a maximum point (the top of the n)
Minimum and maximum points are both examples of turning points

How do I sketch a quadratic graph?

We could create a table of values for the function and then plot it accurately, however we often only require a sketch to be drawn, showing just the key features
The most important features of a quadratic are
- Its overall shape; a u-shape or an n-shape
- Its $y$ -intercept
- Its $x$ -intercept(s), these are also known as the roots
- Its minimum or maximum point (turning point)
If it is a positive quadratic ( $a$ in $a x^{2} + b x + c$ is positive) it will be a u-shape
If it is a negative quadratic ( $a$ in $a x^{2} + b x + c$ is negative) it will be an n-shape
The $y$ -intercept of $y = a x^{2} + b x + c$ will be $(0, c)$
The roots, or the $x$ -intercepts will be the solutions to $y = 0$ ; $a x^{2} + b x + c = 0$
- You can solve a quadratic by factorising, completing the square, or using the quadratic formula
- There may be 2, 1, or 0 solutions and therefore 2, 1, or 0 roots
The minimum or maximum point of a quadratic can be found by;
- Completing the square
  - Once the quadratic has been written in the form $y = p {(x - q)}^{2} + r$ , the minimum or maximum point is given by $(q, r)$
  - Be careful with the sign of the x-coordinate. E.g. if the equation is $y = {(x - 3)}^{2} + 2$ then the minimum point is $(3, 2)$ but if the equation is $y = {(x + 3)}^{2} + 2$ then the minimum point is $(- 3, 2)$
- Using differentiation
  - Solving $\frac{d y}{d x} = 0$ will find the $x$ -coordinate of the minimum or maximum point
  - You can then substitute this into the equation of the quadratic to find the $y$ -coordinate

Worked Example

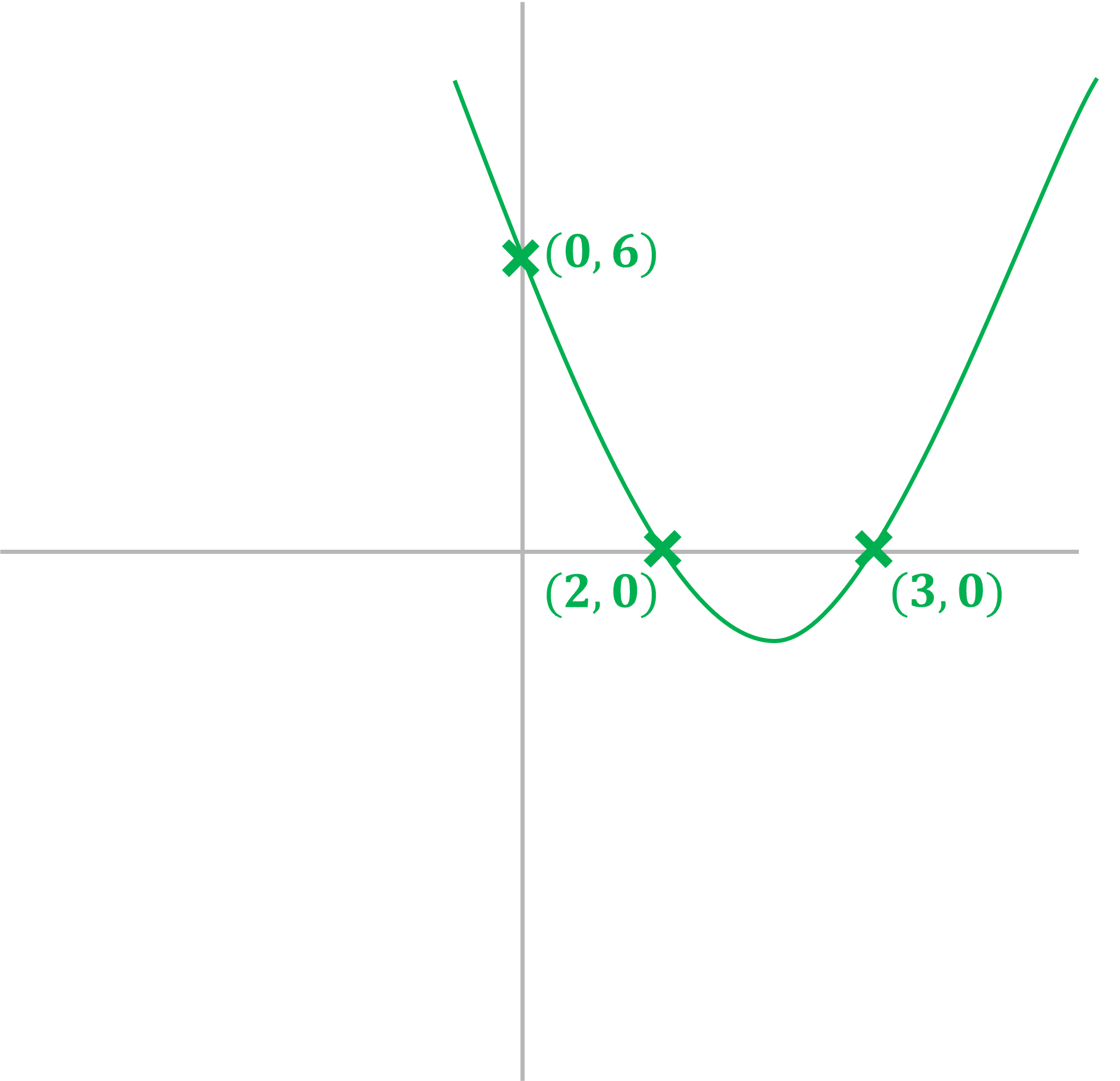
a) Sketch the graph of $y = x^{2} - 5 x + 6$ showing the $x$ and $y$ intercepts

It is a positive quadratic, so will be a u-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the $y$ -axis at (0,6)

Factorise

$y = (x - 2) (x - 3)$

Solve $y = 0$

$(x - 2) (x - 3) = 0$

$x = 2 or x = 3$

So the roots of the graph are

(2,0) and (3,0)

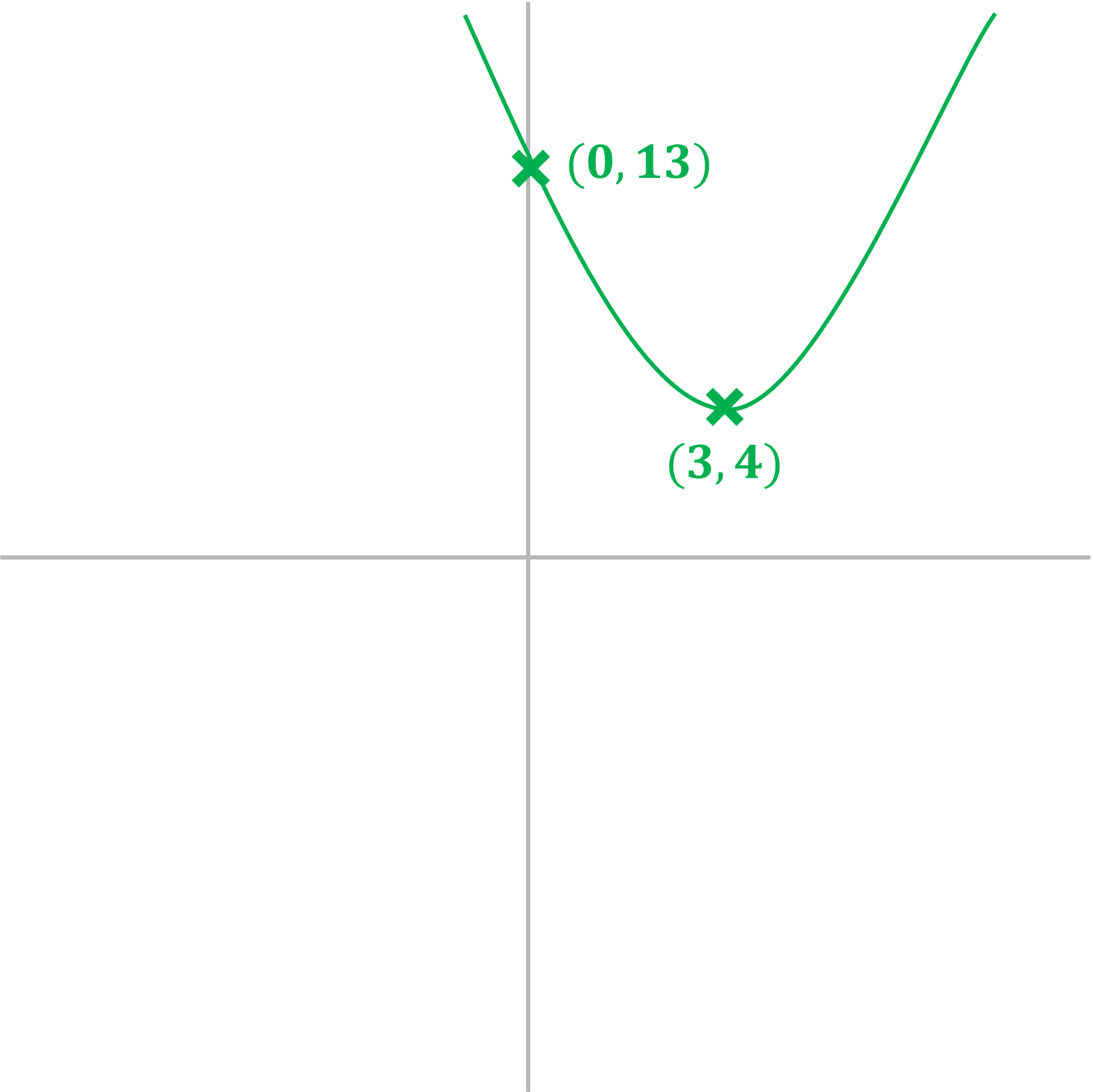
b) Sketch the graph of $y = x^{2} - 6 x + 13$ showing the $y$ -intercept and the turning point

It is a positive quadratic, so will be a u-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the y-axis at

(0,13)

We can find the minimum point (it will be a minimum as it is a positive quadratic) by completing the square:

$x^{2} - 6 x + 13 = {(x - 3)}^{2} - 9 + 13 = {(x - 3)}^{2} + 4$

This shows that the minimum point will be

(3,4)

As the minimum point is above the $x$ -axis, this means the graph will not cross the $x$ -axis i.e. it has no roots

We could also show that there are no roots by trying to solve $x^{2} - 6 x + 13 = 0$

If we use the quadratic formula, we will find that $x$ is the square root of a negative number, which is not a real number, which means there are no real solutions, and hence no roots

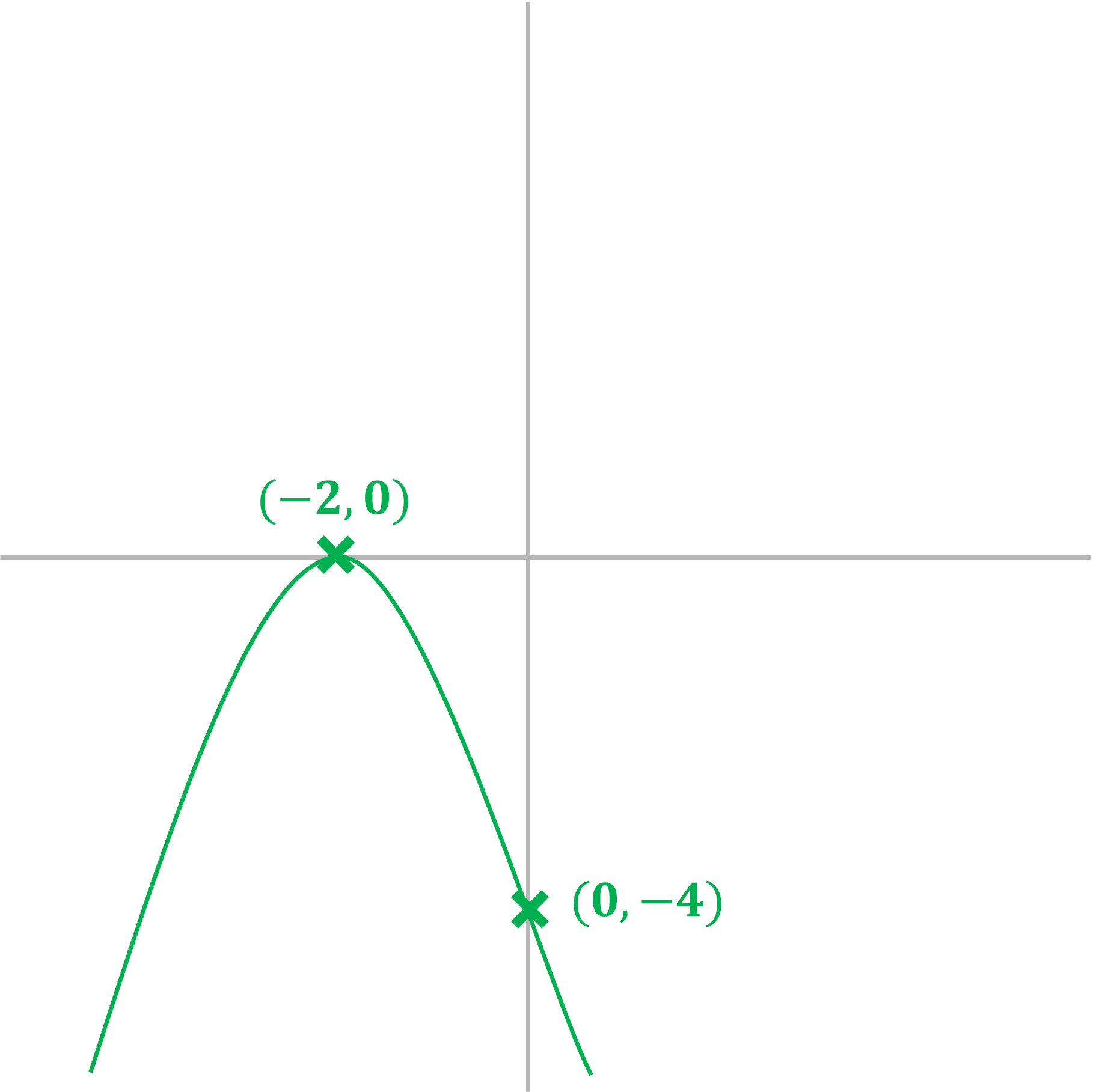
c) Sketch the graph of $y = - x^{2} - 4 x - 4$ showing the root(s), $y$ -intercept, and turning point

It is a negative quadratic, so will be an n-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the $y$ -axis at (0, -4)

We can find the maximum point (it will be a maximum as it is a negative quadratic) by completing the square:

$- x^{2} - 4 x - 4 = - 1 (x^{2} + 4 x + 4) = - 1 ({(x + 2)}^{2} - 4 + 4) = - {(x + 2)}^{2}$

This shows that the maximum point will be

(-2, 0)

As the maximum is on the $x$ -axis, there is only one root

We could also show that there is only one root by solving $- x^{2} - 4 x - 4 = 0$

If you use the quadratic formula, you will find that the two solutions for $x$ are the same number; in this case -2

Polynomial Graphs

What is the graph of a polynomial?

Remember a polynomial is any finite function with non-negative indices, that could mean a quadratic, cubic, quartic or higher power

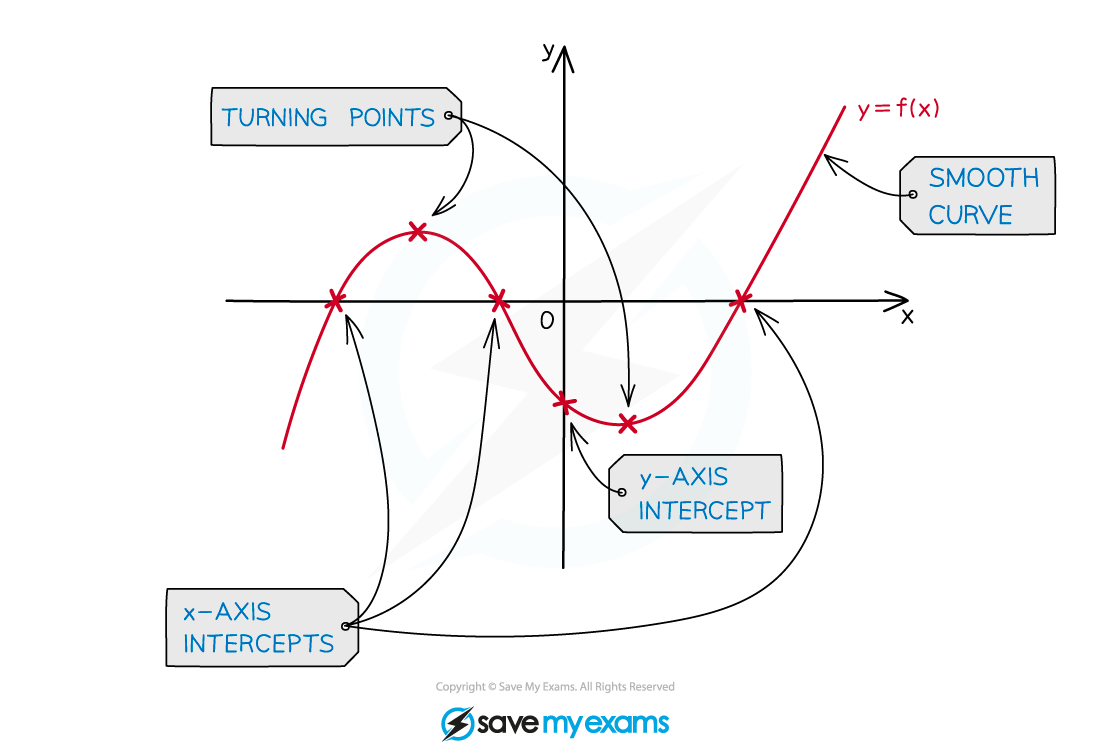
Sketching Polynomials Notes Diagram 1, A Level & AS Level Pure Maths Revision Notes

When asked to sketch a polynomial you'll need to think about the following
- y-axis intercept
- x-axis intercepts (roots)
- turning points (maximum and/or minimum)
- a smooth curve (this takes practice!)

How do I sketch a graph of a polynomial?

STEP 1 Find the y-axis intercept by setting x = 0

STEP 2 Find the x-axis intercepts (roots) by setting y = 0

STEP 3 Consider the shape and “start”/”end” of the graph

eg. a positive cubic graph starts in third quadrant (bottom left) and “ends” in first quadrant (top right)
Whereas a negative cubic graph starts in the second quadrant (top left) and ends in the fourth quadrant (bottom right)

STEP 4 Consider where any turning points should go

STEP 5 Draw with a smooth curve

Sketching Polynomials Notes Diagram 2, A Level & AS Level Pure Maths Revision Notes

Sketching Polynomials Notes Diagram 3, A Level & AS Level Pure Maths Revision Notes

How do I sketch a polynomial from its turning points?

Turning points are where the gradient of the graph is equal to zero
- They are either a minimum; a u-shape
- Or a maximum; an n-shape
The turning points of a polynomial may be found by using differentiation, or you may be told them in the question
First consider the order (power) of the polynomial you are sketching
This will tell you the general shape of the graph, and how many turning points there are likely to be
- A quadratic will have 1 turning point
  - A positive quadratic will have a minimum
  - A negative quadratic will have a maximum
- A cubic will have either 2 or 0 turning points
- A quartic will have either 3 or 1 turning points
Knowing the type of turning point is also useful
- For a maximum
  - The graph will be increasing (going upwards from left to right) before the maximum
  - The graph will be decreasing (going downwards from left to right) after the maximum
- For a minimum
  - The graph will be decreasing before the minimum
  - The graph will be increasing after the minimum
- Putting a point on your sketch where each turning point is, and sketching a small u for a minimum, or a small n for a maximum will help to then fill in the overall shape of the graph

Worked Example

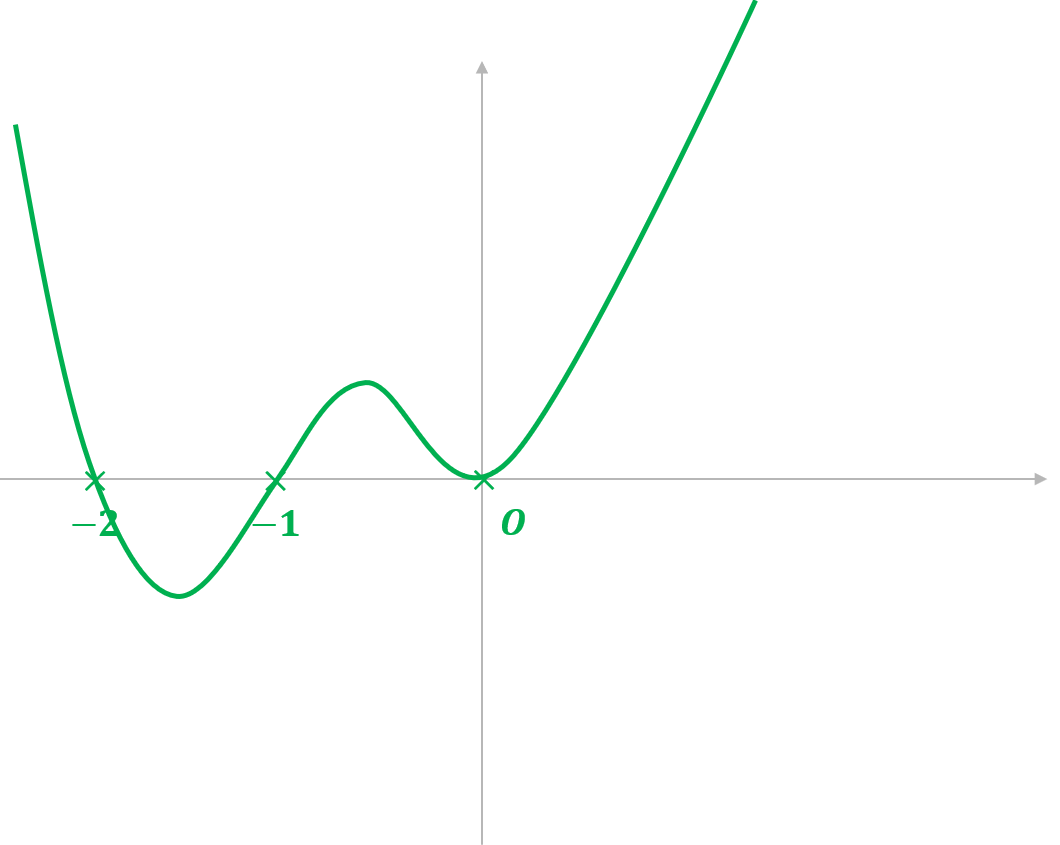
Sketch the graph of $y = 3 x^{4} + 9 x^{3} + 6 x^{2}$ .

Find the coordinates of the $y$ -intercept by setting $x$ equal to 0 and finding the value of $y$ .

$y = 3 {(0)}^{4} + 9 {(0)}^{3} + 6 {(0)}^{2} y = 0$

The coordinates of the $y$ -intercept are (0,0).

Find the coordinates of the $x$ -intercept by setting $y$ equal to 0 and solving to find the values of $x$ .

$3 x^{4} + 9 x^{3} + 6 x^{2} = 0$

Factorise $3 x^{2}$ out of each term in the expression.

$3 x^{2} (x^{2} + 3 x + 2) = 0$

Factorise the quadratic.

$3 x^{2} (x + 1) (x + 2) = 0$

Solve to find the values of $x$ .

$x = 0, x = - 1, x = - 2$

So the graphs crosses the $x$ -axis at the points (-2, 0) and (-1, 0) and touches the axis at the point (0, 0) ( $x = 0$ is a repeated root). Plot each of these points and then join them up with a smooth curve.

Check that the shape of the graph is correct, the given polynomial is a positive quartic, so the shape and number of solutions is correct.

aqa-fm-shketching-polynomials-rn-diagram-we-solution-1

Worked Example

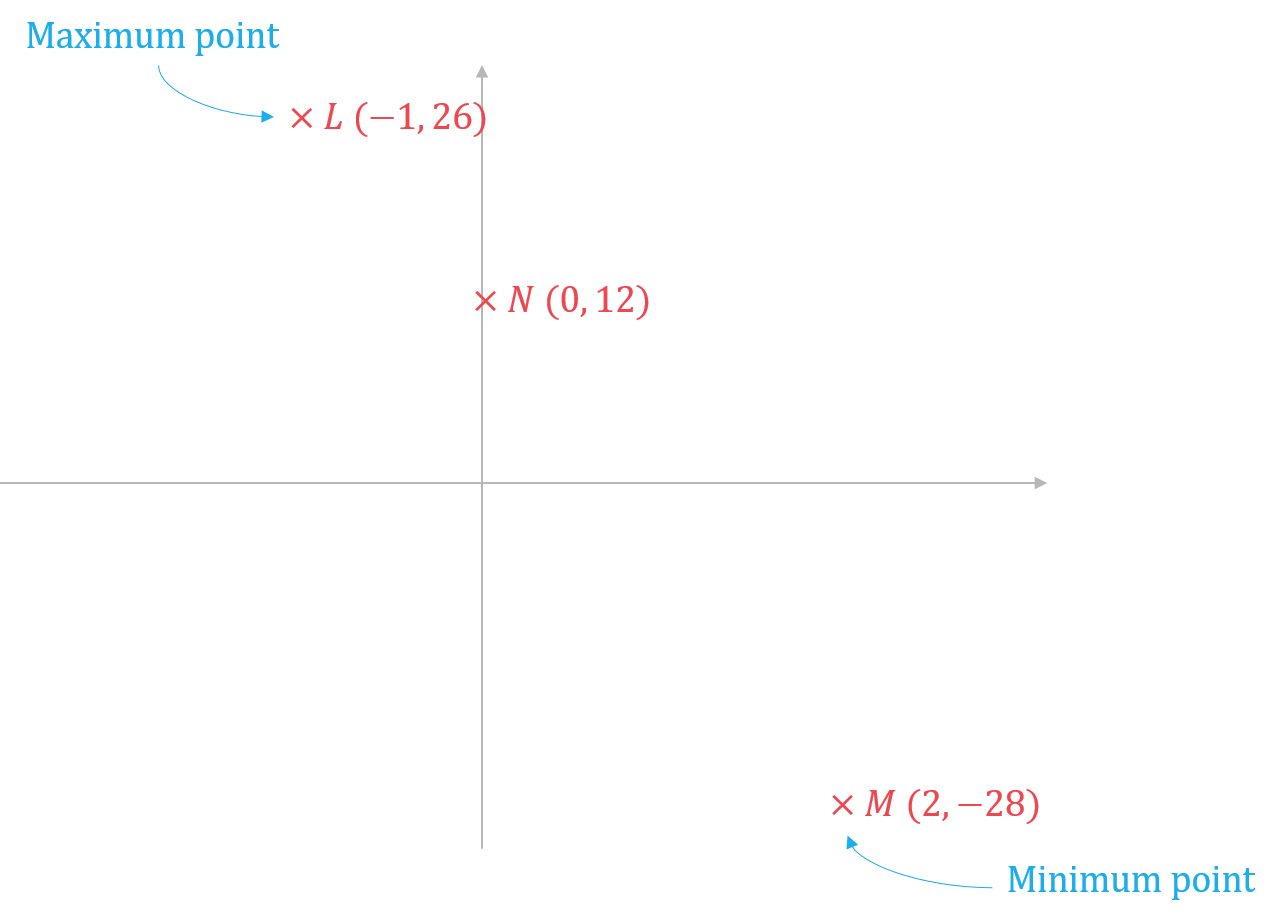
The curve $y = 4 x^{3} - 6 x^{2} - 24 x + 12$ has:

A maximum point at L ( -1, 26 )
A minimum point at M ( 2, -28 )

The curve intersects the $y$ -axis at N.

The curve crosses the $x$ -axis at three distinct points.

Sketch the curve, labelling the points L, M, and N.

Find the coordinates of N by setting $x$ equal to 0 and finding the value of $y$ .

$y = 4 {(0)}^{3} - 6 {(0)}^{2} - 24 (0) + 12 y = 12 N (0, 12)$

The coordinates of the points where the curve crosses the $x$ -axis are not needed, but you should make sure your curve crosses it three times and use the given minimum and maximum points to help you see where.

Plot the points L (-1, 26), M (2, -28) and N (0, 12).

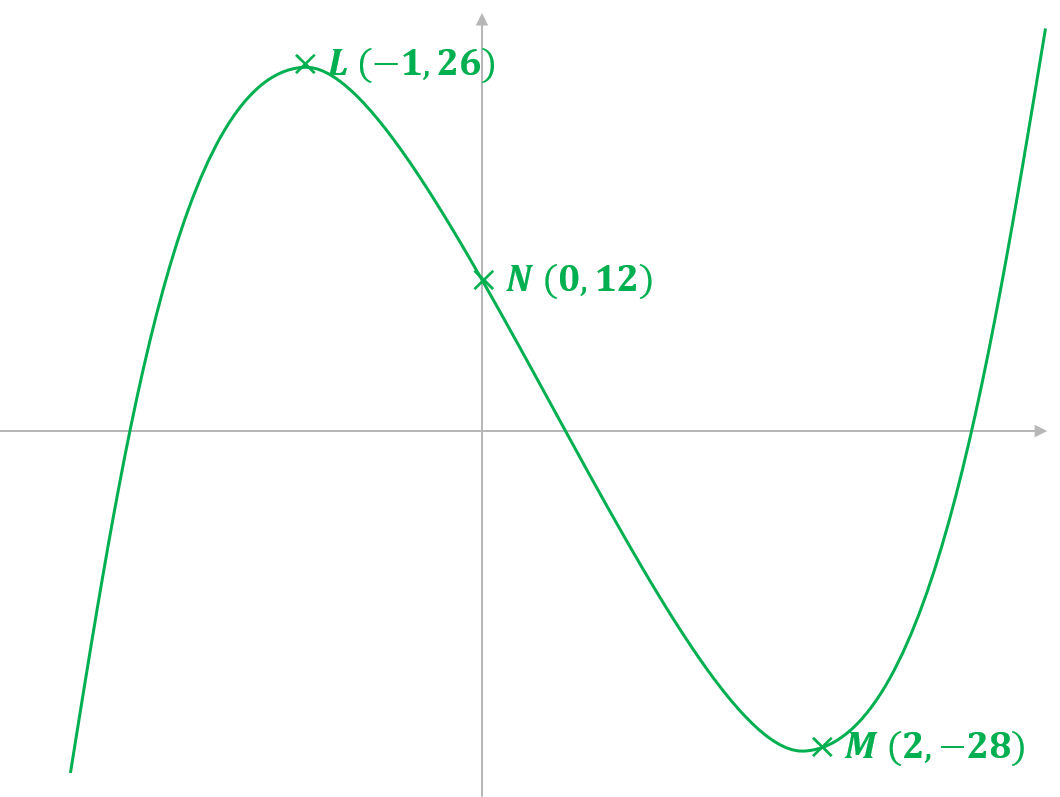
Draw the graph by joining up the points with a smooth curve. Make sure the point L is a maximum (graph changes from increasing to decreasing) and the point M is a minimum (graph changes from decreasing to increasing).

Make sure the graph goes through the $x$ -axis three times.

aqa-fm-shapes-of-graphs-rn-diagram-we-solution

Last updated: 4 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Applications of Factor TheoremNext:Exponential Graphs

Quadratic & Polynomial Graphs (AQA GCSE Further Maths)

Revision Note

Quadratic Graphs

What does a quadratic graph look like?

How do I sketch a quadratic graph?

Worked Example

Polynomial Graphs

What is the graph of a polynomial?

How do I sketch a graph of a polynomial?

How do I sketch a polynomial from its turning points?

Worked Example

Worked Example

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Jamie Wood

Author: Dan Finlay