GCSEFurther MathsAQARevision Notes2. Algebra & FunctionsAlgebra ToolkitForming & Solving Equations

Forming & Solving Equations (AQA GCSE Further Maths)

Revision Note

Test yourself
Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Algebraic Ratio & Percentages

How do I change ratios and percentages into algebra?

  • If x colon y equals a colon b then x over y equals a over b

    • the equals sign now allows you to use algebra

  • x percent sign of ycan be written x over 100 cross times y

    • this simplifies to fraction numerator x y over denominator 100 end fraction

  • An increase of a percent sign on b can be written open parentheses 1 plus a over 100 close parentheses cross times b

    • this can also be written b open parentheses 1 plus a over 100 close parentheses

Worked Example

Let A equals 6 x and let B equals x plus 1.

Find the value of x in each of the cases below.

(a) A colon B equals 9 colon 2 
 
As A colon B space equals space 9 colon 2, it is also true that 

A over B equals 9 over 2 

Substituting in the expressions for A and B 

fraction numerator 6 x over denominator x plus 1 end fraction equals 9 over 2 

Now we need to solve the equation for x
Multiply both sides by 2, and then by open parentheses x plus 1 close parentheses 

table row cell fraction numerator 2 open parentheses 6 x close parentheses over denominator x plus 1 end fraction end cell equals 9 row cell 2 open parentheses 6 x close parentheses end cell equals cell 9 open parentheses x plus 1 close parentheses end cell end table 

Simplify and solve

table row cell 12 x end cell equals cell 9 x plus 9 end cell row cell 3 x end cell equals 9 end table 

bold italic x bold equals bold 3

(b) A percent sign of 50 equals B percent sign of 250

 

As A percent sign of 50 = B percent sign of 250, we can write that 

A over 100 cross times 50 equals B over 100 cross times 250 

Substituting in the expressions for A and B 

fraction numerator 6 x over denominator 100 end fraction cross times 50 equals fraction numerator x plus 1 over denominator 100 end fraction cross times 250 

Now we need to solve the equation for x 
Multiply both sides by 100 to remove the fractions

6 x cross times 50 equals open parentheses x plus 1 close parentheses cross times 250 

Multiply out both sides, and then solve for x 

table attributes columnalign right center left columnspacing 0px end attributes row cell 300 x end cell equals cell 250 x plus 250 end cell row cell 50 x end cell equals 250 end table 

bold italic x bold equals bold 5

Forming & Solving Equations

Before solving an equation you may need to form it from the information given in the question.

How do I form an expression or equation?

  • An expression is an algebraic statement without an equals sign e.g. 3 x plus 7 or 2 left parenthesis x squared minus 14 right parenthesis

  • Sometimes we need to form expressions to help us express unknown values

  • If a value is unknown you can represent it by a letter such as x

  • An equation is simply an expression with an equals sign that can then be solved

  • For example

    • If Adam is 10 years younger than Barry and the sum of their ages is 25, you can find out how old each one is

      • Represent Adam's age as x then Barry's age is x plus 10

      • We can solve the equation x plus x plus 10 space equals space 25 or 2 x plus 10 space equals space 25

  • Sometimes you might have two unrelated unknown values (x and y) and have to use the given information to form two simultaneous equations

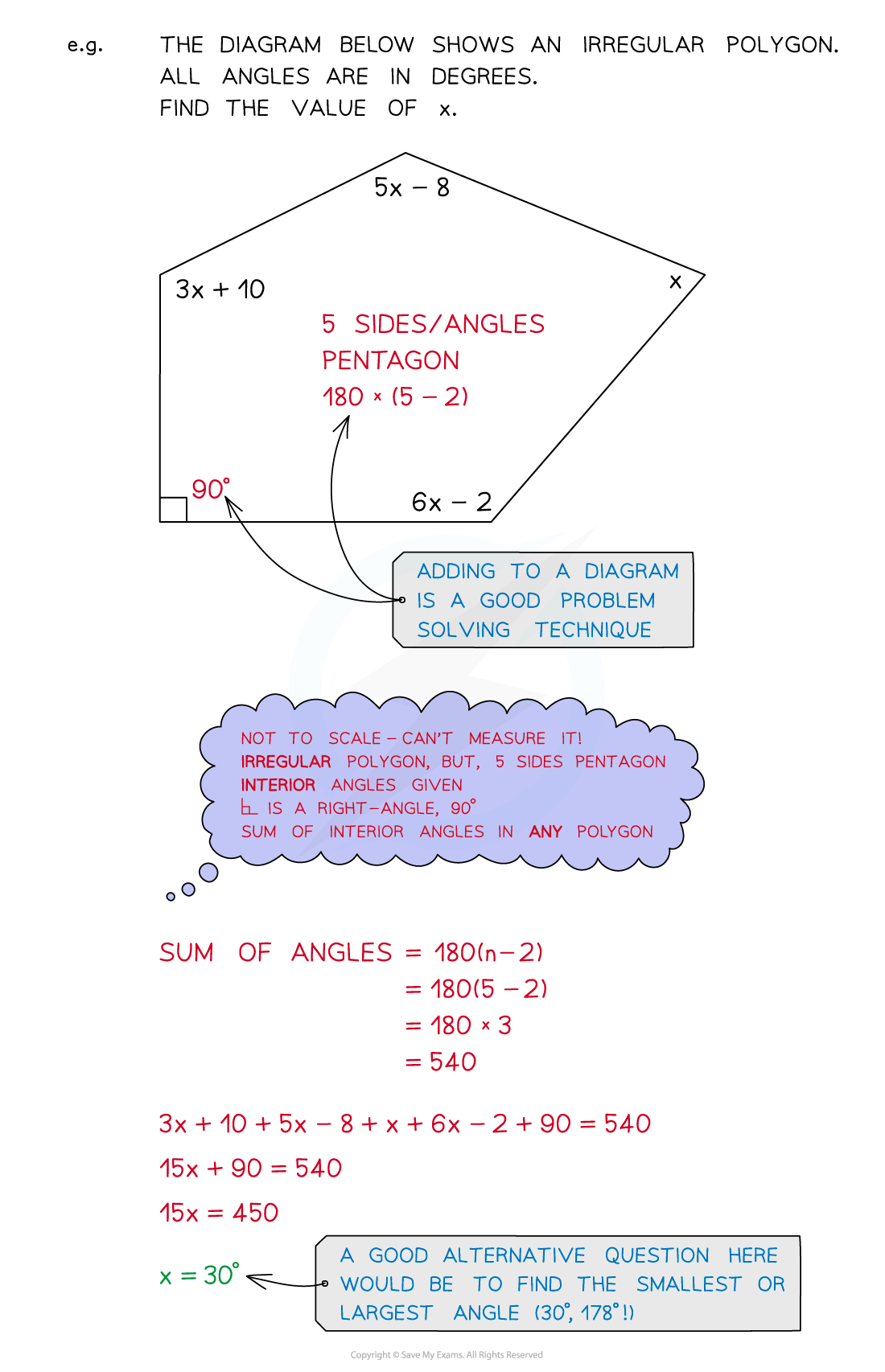
Many questions involve having to form and solve equations from information given about things relating to shapes, like lengths or angles.

How do I form an equation involving a 2D shape?

  • If no diagram is given it is almost always a good idea to quickly sketch one

  • Add any information given in the question to the diagram

    • This information will normally involve expressions in terms of one or two variables

  • If the question involves perimeter, figure out which sides are equal length

    • If a triangle is given, are any of the sides equal length?

  • If the question involves area, write down the necessary formula for the area of that shape

    • If it is an uncommon shape you may need to split it up into two or more common shapes that you can work out areas for

    • this is often called compound area in GCSE Mathematics courses

  • Remember that a regular polygon means all the sides are equal length

    • For example, a regular pentagon with side length 2x – 1 has 5 equal sides so its perimeter is 5(2x – 1)

  • If one of the shapes is a circle or part of a circle, use π throughout rather than multiplying by it and ending up with long decimals

  • Consider the properties of angles within the given shape to decide which sides will have equal lengths

    • If a triangle is given, how many of the angles are equal?

      • An isosceles triangle has two equal angles

      • An equilateral triangle has three equal angles

    • Consider angles in parallel lines (alternative, corresponding, co-interior)

    • In a parallelogram or rhombus, opposite angles are equal and all four sum to 360°

    • A kite has one equal pair of opposite angles

  • If the question involves angles, use the formula for the sum of the interior angles of a polygon

    • For a polygon of n sides, the sum of the angles will be 180°×(n - 2)

    • Remember that a regular polygon means all the angles are equal

  • You may also have to use circle theorems to spot which angles are equal to each other, or to spot right-angles

EPS Notes fig4

How do I form an equation involving the surface area or volume of a 3D shape?

  • If no diagram is given it is almost always a good idea to quickly sketch one

  • Add any information given in the question to the diagram

    • This information will normally involve expressions in terms of one or two variables

  • Consider the properties of the given shape to decide which sides will have equal lengths

    • In a cube all sides are equal

    • All prisms have the same shape (cross section) at the front and back

  • If the question involves volume, write down the necessary formula for the volume of that shape

    • If it is an uncommon shape the exam question will give you the formula that you need

  • It the question involves surface area,

    • Remember to consider any faces that may be hidden in the diagram

      • STEP 1
        Write down the number of faces the shape has and if any are the same

      • STEP 2
        Identify the 2D shape of each face and write down the formula for the area of each one

      • STEP 3
        Substitute the given expressions into the formula for each one

      • STEP 4
        Add the expressions together, double checking that you have one for each of the faces

Examiner Tips and Tricks

  • Do not start by focusing on what the question has asked you to find, but on what maths you can do

  • If your attempt turns out to be unhelpful, that’s fine, you may still pick up some marks

  • If your attempt is relevant it could nudge you towards the full solution – and full marks!

  • Add information to a diagram as you work through a problem

    • If there is no diagram, try sketching one

Worked Example

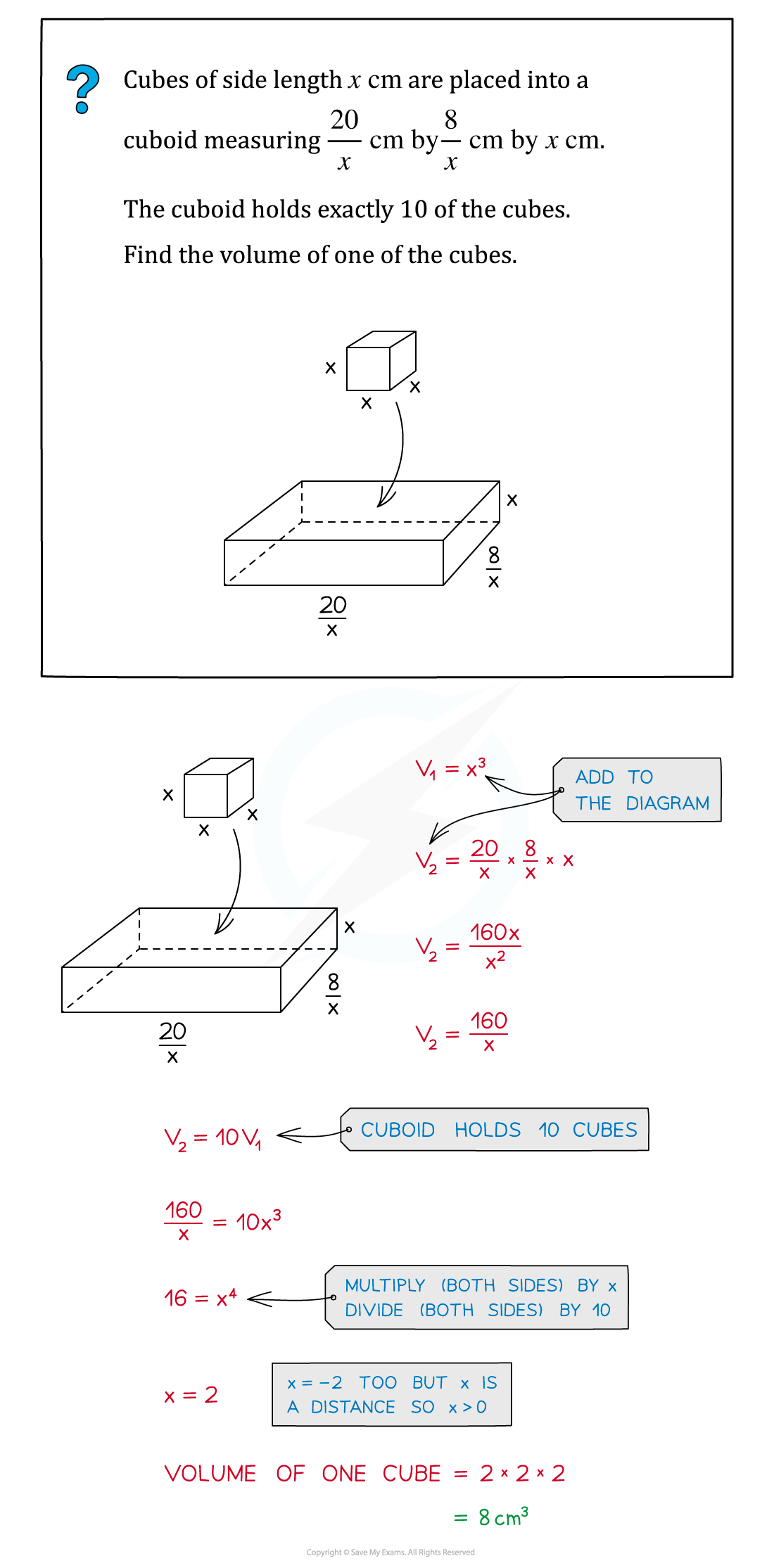
EPS Example fig2 sol, downloadable IGCSE & GCSE Maths revision notes

Worked Example

The base radius, r, of a cone is the same as the radius of a hemisphere. The total surface area of the cone is equal to the total surface area of the hemisphere. 

The surface area of a sphere is given by 4 πr squared.
The curved surface area of a cone is given by pi r l.

 

(a) Find the slant height, l, of the cone in terms of r.

 

Find an expressions for the surface area of the hemisphere in terms of l and r.
Remember that a hemisphere has both a curved surface area and a flat circular face so the formula for the surface area is:

Surface area of hemisphere = 1 half cross times space 4 pi r squared space plus pi r squared space equals space 3 pi r squared

Find an expressions for the surface area of the cone in terms of l and r.
Remember that a cone has both a curved surface area and a flat circular face so the formula for the surface area is:

Surface area of cone = pi r l space plus pi r squared space equals space pi r open parentheses l space plus space r close parentheses

The surface areas are equal, so set these two formulae equal to each other.

3 pi r squared space equals space pi r open parentheses l space plus space r close parentheses 

Rearrange to make l the subject.

Begin by dividing both sides by pi r.

table row cell 3 up diagonal strike pi r end strike squared space end cell equals cell space up diagonal strike pi r end strike open parentheses l space plus space r close parentheses end cell row cell 3 r space end cell equals cell space l space plus space r end cell end table

bold italic l bold space bold equals bold space bold 2 bold italic r

  

(b) Given that r space equals space 19 cm, find the curved surface area of the cone.
Give your answer accurate to 1 decimal place.

 

Use your answer from part (a) to find the value of l, by substituting r space equals space 19 into l space equals space 2 r. 

l space equals space 2 r space equals space 2 space cross times space 19 space equals space 38 space cm   

Substitute r space equals space 19 and l space equals space 38 into the formula for the curved surface area of the cone. 

Note that this is not for the whole surface area.

pi r l space equals space pi space cross times space 19 space cross times space 38 space equals space 722 straight pi space equals space 2268.229.... space 

Round your answer to 1 decimal place. 
The first decimal place is a 2, and this is followed by a 2 so you do not need to round it up. 

bold Curved bold space bold surface bold space bold area bold space bold equals bold space bold 2268 bold. bold 2 bold space bold cm to the power of bold 2 bold space bold space stretchy left parenthesis 1 space d. p. stretchy right parenthesis

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Equating CoefficientsNext:Binomial Expansion
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.